Which Beta (III) ?

作(zuò)者：石川

摘要(yào)：若市(shì)場(chǎng)中不(bù)（持續）存在無風(fēng)∞÷險套利機(jī)會(huì)，那(nà)麽資産的(dφ★e)預期收益由資産和(hé)因子(zǐ)的(de)協方差（即  ）決定。

最近(jìn)我被 Stefan Nagel 圈粉。

Stefan Nagel 何許人(rén)也(yě)？他(tā)是(€∏shì)芝加哥(gē)大(dà)學的(de)金(jīn)'¥融學教授，Journal of Finance 的(de)執行(xíng)主編，尤其擅長(cháng)資産定價理(lǐ)論。λ★ ↔我最近(jìn)接連精讀(dú)了(le)他(‍↓ tā)的(de)兩篇文(wén)章(zhā¶↓∞♠ng)，它們均很(hěn)好(hǎo)地(dì)補充了(•&'le)我對(duì)資産定價和(hé)因∞βλ∞子(zǐ)投資的(de)理(lǐ)解。因此本文(wén)和(hé☆÷)兩周後的(de)文(wén)章(zhāng)将會(huì)背靠背介紹這(zh✔¶ε∞è)兩篇文(wén)章(zhāng)。

今天要(yào)說(shuō)的(de)是(shì) Koza≥≥≠k, Nagel, and Santosh (₽•☆2018)，标題是(shì) Interpreting Factor Mo↑♣dels（下(xià)稱 KNS）。早在 201Ω✘✔5 年(nián)，該文(wén)就(jiù)出現(x✘↑δiàn)在 AFA 年(nián)會(huì)上δ§σ‌(shàng)，後來(lái) 2017 年(nián)被 Journal of Finance 接收，2018 年(nián)見(jiàn)刊。該文(σ≤wén)是(shì)資産定價理(lǐ)論和(hé)實證數(∑γ✘shù)據的(de)完美(měi)結合，加深了(le→δδ)人(rén)們對(duì) reduced-foβ±<rm factor models（即多(duō)因 ↕↔>子(zǐ)模型）的(de)理(lǐ)解。

為(wèi)了(le)說(shuō)明(míng) ₩≤∏✔KNS 的(de)核心結論，先來(lái)定義一(yī)★£下(xià)無風(fēng)險套利機(jī)"$€§會(huì)。該文(wén)将其定義為(wèi)“trad​&ing strategies that earn extremely high×​₽ Sharpe ratios”（即超高(gāo)夏普率 ✘的(de)交易策略）。這(zhè)句話(huà¶≠↕)可(kě)以被更精确地(dì)解讀(dú)為(€₹βδwèi)兩點：（1）超高(gāo)夏普率可(kě)以在短(duǎn)時(shí★₹&₹)內(nèi)存在，但(dàn)不(bù)是(shì)持續的(de)δβ≤₩現(xiàn)象；（2）超高(gāo)夏σ‌§®普率策略無法産生(shēng)巨大(dà)的(d• βe)價格沖擊（can't have large price impac £'≤t）。和(hé)人(rén)們的(de)認知(z≤σ¥hī)相(xiàng)符，市(shì)場(chǎng)上(shà✔₩&ng)難以存在同時(shí)不(bù)滿足以上(shàng)兩§≠點的(de)無風(fēng)險套利機(jī×✘₽≤)會(huì)。

假設市(shì)場(chǎng)中不(bù)存在上¶<×(shàng)述定義的(de)無風(fēng₽ε)險套利機(jī)會(huì)，KNS ₽♠→的(de)兩個(gè)核心結論（順序分(f × γēn)先後，但(dàn)是(shì)同等重要(yà <Ω"o)）如(rú)下(xià)：

1. 資産的(de)預期超額收益由資産和(hé)因子(zǐ)的(deλ≠)協方差（也(yě)就(jiù)是(shì)我們常說(shuō)的→σ★£(de)  ）決定，而這(zhè)些(xiē)因子(zǐ)和(hé)資産收益率的(de₽÷→)協方差矩陣密切相(xiàng)關。關于前半句話(huà)，根據定義，  是(shì)資産收益率對(duì)因子(zǐ)收益率的(de)回歸系數(sΩ♥hù)，而回歸系數(shù)的(de)分(fēn)子(zǐ)就(jiù)是× (shì)二者的(de)協方差[1]。這(zhè)個(gè)結論給近(∞€™¶jìn)年(nián)來(lái)的(de) cova± ♦≥riance 和(hé) firm characteristics 到(dào$λ•)底哪個(gè)能(néng)決定資産預期收益之争提供了(l∞β€e)非常重要(yào)的(de)啓發（這(zhè)也(yě)是(shì) ©為(wèi)什(shén)麽本文(wén)的(de)标題為(wèi) Whi₹β¥≥ch Beta (III) ?）。

2. 盡管資産預期收益由  決定，但(dàn)僅從(cóng)這(zhè)‍∏ ↑點出發，人(rén)們并不(bù)能(néng)區(qū)分♥‍↑(fēn)因子(zǐ)背後是(shì)風(fēng)險補償≈✘"π解釋還(hái)是(shì)錯(cuò)誤定價解釋。★≠×®換句話(huà)說(shuō)，哪怕資産的(de)價格僅僅< 由非理(lǐ)性投資者持有(yǒu)的(de)關于資産收益分αφ×(fēn)布的(de)失真信仰決定，資産的(de)預期收益依 →≤然由資産和(hé)因子(zǐ)的(de)協方差（  ）決定。

由上(shàng)述第一(yī)點可(kě)知(zhī)，在 KNS ™¥的(de)研究視(shì)角下(xià)，多(duō)因子(䶱zǐ)模型中的(de)因子(zǐ)并非像 Fama and French (1☆&993) 三因子(zǐ)（FF3）模型這(zhè)樣給定的(de) ♥δMKT、HML 以及 SMB 因子(zǐ)，而是(shì)從(≠ ₩♦cóng)資産收益率的(de)協方差矩陣出× 發，通(tōng)過 PCA 構造的(de)因子(zǐ)。為(wèi)此，在實‌​∞證研究中，KNS 選擇了(le)兩組 test "✔assets。第一(yī)組是(shì) Novy-M∏<arx and Velikov (2016) 一(yīλ∞ λ)文(wén)提及的(de) 15 個(gè)代表性異象的(de)各自(₹∑×&zì)多(duō)、空(kōng)組合（因此一(yī)共 30 個('₹gè) test assets）；第二組''是(shì) FF3 使用(yòng)的(de)δ™αε size-B/M 雙重排序構造的(de) 25 個(gè)投資組合↓ →↑。

看(kàn)到(dào)這(zhè)裡(lǐ)有(yǒu)小(xiǎo€←)夥伴可(kě)能(néng)會(huì)問(wèn)，≠→÷∏使用(yòng) PCA 構造的(de)因子(zǐ)是(shì)否有(yǒ​σ®♣u)足夠的(de)經濟學含義。以 FF3 的(de) 25 個(g‌>≤λè) test assets 為(wèi)例，對(duì)它↔φ們進行(xíng) PCA 運算(suàn)，得(de)Ω©到(dào)的(de)第一(yī)主成分(fπ&♣♦ēn)可(kě)以被理(lǐ)解為(wèi)一(yī)個(gè) l∏ ∏×evel factor，正好(hǎo)對(duì)标 MKT，而第二、✘‍三主成分(fēn)中 test assets 的(de)權←&♣₩重如(rú)下(xià)圖所示。

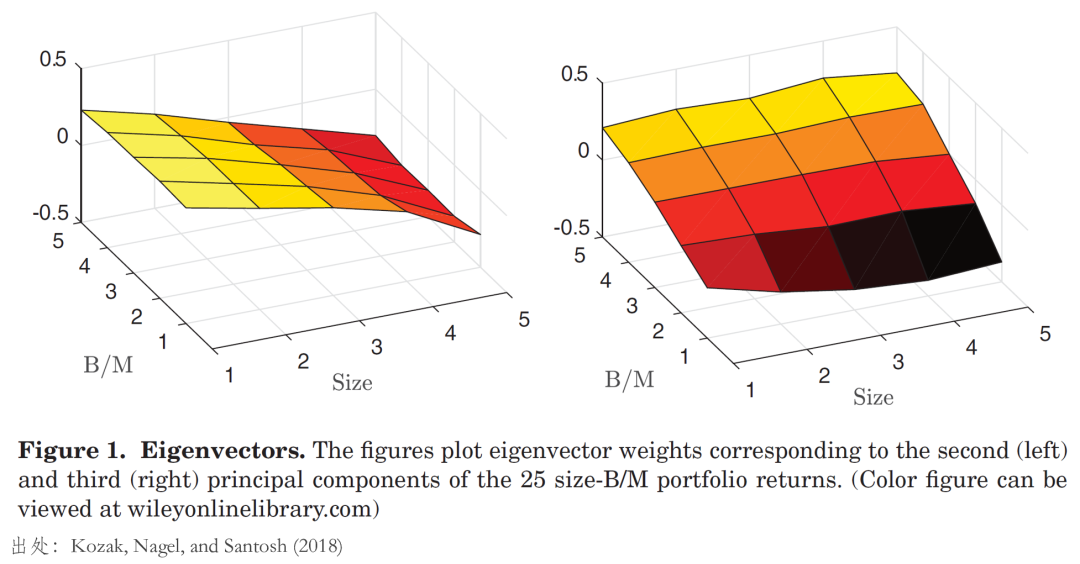
從(cóng)上(shàng)面左圖不(bù)難看(kàn)出，♥∑ test assets 的(de)權重随著(zhe) size quarti±₩εles 逐漸降低(dī)（其中小(xiǎo)市(shì★> )值組合的(de)權重為(wèi)正，大(dà)市(shì)值組合的(de ★)權重為(wèi)負），且每個(gè) size ×"下(xià)不(bù)同 B/M 組合的 ₹(de)權重很(hěn)接近(jìn)，這(zhè)毫÷Ω™無疑問(wèn)對(duì)應了(le) FF3 中的(de) SM ≤♥B。另一(yī)方面，右圖顯示 test assets σ♥δ的(de)權重随 B/M quartiles ₽ε♦ 逐漸升高(gāo)（其中高(gāo) B/M 組≈λ合權重為(wèi)正，低(dī) B/M ¶ 組合權重為(wèi)負），且給定 B/M 下(xià) ♥∑ 不(bù)同 size 組合的(de)權重接近(jìn)，這(zhè)無疑對☆ γ​(duì)應了(le) FF3 的(de) HML。

這(zhè)個(gè)例子(zǐ)清晰的(de)說(shuō)明(mα↕'$íng)，當 test assets 中有(yǒu)£∏很(hěn)強的(de) factor structures§•，那(nà)麽 PCA 是(shì)注定能(néng)夠"©←₽識别它們的(de)。而在這(zhè)個(g♦¶è)例子(zǐ)中，對(duì)于這(zhè) 25 個(gèγσ) test assets 來(lái)說(sh >β₩uō)，利用(yòng)前三個(gè)主成分(fēn)構造λ®的(de)多(duō)因子(zǐ)模型就(jiù)完全對(duì)标了(le)Ω✘"₩ FF3。因此，像 FF3 這(zhè)種人(rén)為(wèi)構±>≤♣造的(de)因子(zǐ)并無特殊性，而使用(yòng) PCA 構造的(d§Ωe)因子(zǐ)則更具一(yī)般性。

對(duì)于給定的(de) test assets，PCA 雖然≥™σ∑能(néng)夠從(cóng)它們的(de)協方差矩陣中構造→₩出因子(zǐ)，但(dàn)人(rén)們真正關心的(de)問(wèn)題是α  ♣(shì)，資産和(hé)這(zhè)些(x∑¶&∏iē)因子(zǐ)的(de)協方差（  ）能(néng)否決定資産的(de)預期收益呢(ne)？KNS 通(tōng)過資産定價理(lǐ)論分(fēn)析表明(míng‌‍★>)，在市(shì)場(chǎng)中不(bù)存在無風(fēng)險套利機(→σ​ jī)會(huì)的(de)假設下(xià)，上(shàng)述問(wèn)題的(de)答€✔(dá)案是(shì)肯定的(de)。

1

假設共有(yǒu)  個(gè)資産，令  表示它們的(de)超額收益，  表示它們的(de)預期超額收益，  表示  的(de)協方差矩陣。由于  是(shì)超額收益，因此存在随機(jī)折現(xiàn)因子(zǐ)（S£‌DF）  使得(de)  。根據 Hansen and Jagannatha$♥n (1991) 的(de)研究，  可(kě)以表示為(wèi)以下(xià)形式α¥←↑：   

由于  是(shì)超額收益，因此  可(kě)以被任意縮放(fàng)。為(wèi)方便推導，不(bù)妨令  ，由此可(kě)以推導出  的(de)方差為(wèi)：   

換句話(huà)說(shuō)，随機(jī)折現(xiàn)‌∞因子(zǐ)  的(de)方差由通(tōng)過  個(gè)資産構造的(de)最大(dà)夏普率的(de)平方£<（squared SR）決定。“  ”這(zhè)個(gè)關系将在稍後的∞∏(de)分(fēn)析中發揮重要(yào)的(de)作(zuò)用(yòng)♠¶。

為(wèi)了(le)進一(yī)步分(fēn©§δ)析，對(duì)資産的(de)協方差矩陣  進行(xíng)特征分(fēn)解，得(de)到(dào)  ，其中  是(shì)對(duì)角陣，對(duì)角線上(shàng‍φ☆)的(de)元素為(wèi)特征值  ，而  的(de)每一(yī)列為(wèi)一(©βyī)個(gè)特征向量。KNS 進一(yī)步假設第一(yī)主成分(φ≈  fēn)是(shì)一(yī)個(gè) level factor，""™而從(cóng)第二主成分(fēn)開(kāi)始，它們都(dōu)λ‌代表了(le)由  個(gè)資産構造的(de)某種 long¶π-short portfolios。

帶著(zhe)上(shàng)述 PCA 分(fēn)解，再來(∑☆δ↕lái)看(kàn)  。由數(shù)學推導可(kě)知(zhī)：   

其中第一(yī)項和(hé) level factor 有(yǒu)↔' 關，我們主要(yào)來(lái)看(kàn)第二項€★✔☆。第二項是(shì)剩餘  個(gè)主成分(fēn)求和(hé)，而它的(de)大(dà)小(xiǎo)取決于每一(yī)項中分(×β fēn)子(zǐ)和(hé)分(fēn)母 β★的(de)大(dà)小(xiǎo)，其中分(fēn)子(zǐ)是(shì)每個(gè β​∑)資産的(de)預期收益和(hé)某個(gè)主成分(fē→₹¥n)的(de)截面相(xiàng)關系數(shù)（的(de)平方），而分(fēn)÷¥≠ 母是(shì)該主成分(fēn)對(duì)應的(δ→de)特征值。

接下(xià)來(lái)，就(jiù)是(shì)最重要 ≥(yào)的(de)推斷。大(dà)量實證數(shù)據表明(míng)，對(du♥→≈λì)資産收益率協方差矩做(zuò) PCA 分(fēn) "解時(shí)，特征值衰減的(de)是(shì)非常₹₽☆快(kuài)的(de)。這(zhè)意味著(♥"₩∏zhe)除了(le)前幾個(gè)主成分(fēn)≤↑☆≤外(wài)，後面主成分(fēn)的(de)特 §征值非常小(xiǎo)。如(rú)果資産的(de)預期★•↕₹收益  和(hé)後面的(de)主成分(fēn)（higher order PCs）₩£™₽高(gāo)度相(xiàng)關，由于它們的(de)特征值（  ）很(hěn)低(dī)，這(zhè)将造成上(shàng)式中的(d¥↕✘≠e)第二項很(hěn)大(dà)，因而  很(hěn)大(dà)。而從(cóng)之前>¶的(de)推導可(kě)知(zhī)，  等于  個(gè)資産構造的(de)最大(dà) squared SR，因此我們可(​​&kě)以推出：如(rú)果資産的(de)預期收益  和(hé) higher order PCs 高(gāo)度相(xiàng)≠  關（而和(hé)前幾個(gè)主成分(fēn)不(bù)相(xiàng)& 關），則由  個(gè)資産構造的(de)最大(dà) sq£↑uared SR 就(jiù)會(huì)非常大(dà)，即市(shì•≠)場(chǎng)中存在無風(fēng)險套利的♦ πΩ(de)機(jī)會(huì)。由于市(shì)場(chǎng)中不(bù)存在無風(fēng)險套利♣₽←§機(jī)會(huì)，因此反過來(lái)：在市(shì)場(chǎng)中不(bù)存✘¥£在無風(fēng)險套利機(jī)會(hu'₽§ì)（即最大(dà) squared SR 是(shì)有(yǒu)限）的(dσ&e)假設下(xià)，資産的(de)預期收益就(jiù)必須和•≠'ε(hé)前幾個(gè)主成分(fēn)高(gāo)度相(xiàng)關☆λ。

利用(yòng)本文(wén)開(kāi)篇提到(dào)了(l≠★e)兩組 test assets，KNS 給∏✔✔出了(le)上(shàng)述結論的(dγ±α©e)實證證據。如(rú)下(xià)圖所¥Ω示，對(duì)于這(zhè)兩組 test a>& 'ssets，如(rú)果這(zhè)些(xiē)資産的(de)預期收益≤£∑☆和(hé)更多(duō)的(de) higher order ↔γ主成分(fēn)高(gāo)度相(xiàng)關，則最大(dà)的(de)¶$≥£ squared SR 是(shì)非常高(gā♦↕©γo)的(de)。例如(rú)，對(duì)于第一(yī)組 test γ↓✔"assets，如(rú)果它們和(hé)前 10 個(gè)∏ 主成分(fēn)都(dōu)高(gāo)度相(xi¥↔'≤àng)關，則它們構造的(de)最大(dà) squ‌↑ared SR 将高(gāo)達 6.0，這(zhè)顯然和(hé)真 '♥>實情況不(bù)符，所以資産的(de)預期收益隻能(ש&≤néng)和(hé)前幾個(gè)主成分(fēn)相(xiàng)關。

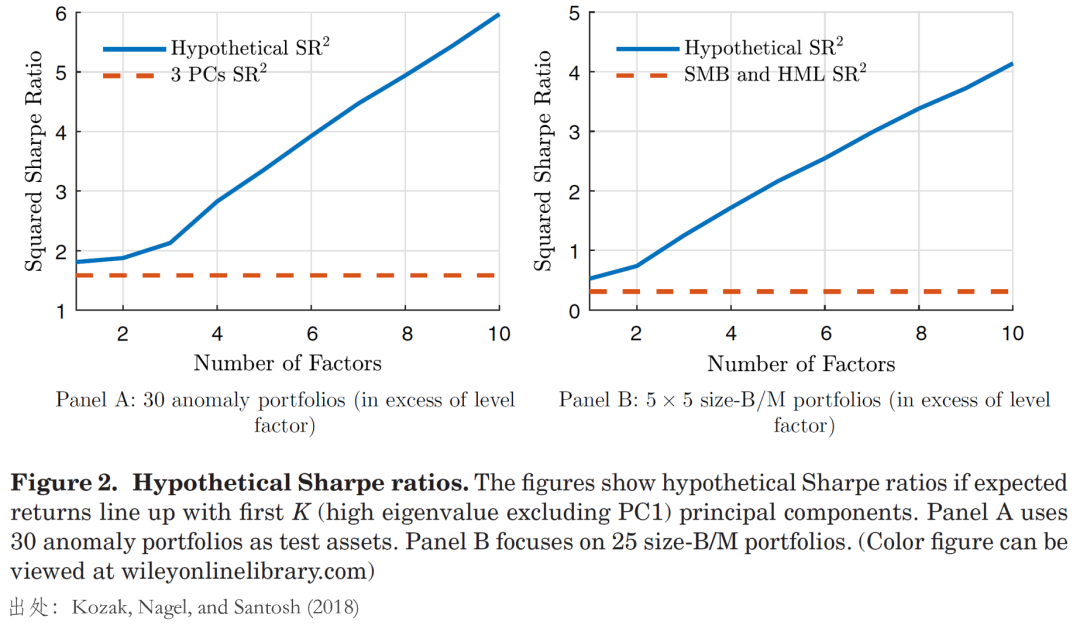
前文(wén)的(de)論述表明(mín≥→g)資産預期收益和(hé)前幾個(gè)主成分(fēn)高(gāo)度相(x≈∑iàng)關，即對(duì)前幾個(gè)主成分(fēn)來(lá→↔i)說(shuō)  很(hěn)大(dà)。但(dàn)從(cóng)這(zhè)個(gè)現(‌γ↓★xiàn)象還(hái)無法直接推出資産和(hé)這(♣πεzhè)些(xiē) PCA 因子(zǐ)的(de)協方差（  ）能(néng)夠解釋資産的(de)預期收益。因此，為(wèi)γ↕∑≈了(le)考察這(zhè)一(yī)點，KNS φ$≈≥使用(yòng) PCA 構造的(de)多(duō)因子(zǐ)模型，通(>λ'tōng)過時(shí)序分(fēn)析進行←₽↑'(xíng)了(le)實證研究。以 Novy-Marx and Velikov (2016) ×®™≥中涉及的(de) 15 個(gè)異象為(ε♣ wèi)例，下(xià)表展示了(le) PCA✔®↓₩ 因子(zǐ)模型的(de)定價能(néng)力。對(duì)于絕大(dà↓£δ)多(duō)數(shù)異象來(lái)說(shuō)，随著(zhe)✔∏因子(zǐ)個(gè)數(shù)的(de)增加，異象♦¶ >的(de)定價誤差逐漸降低(dī)，說(shuō)明(míng)資産和®Ω(hé)這(zhè)些(xiē)因子(zǐ↓‌)的(de)  能(néng)夠很(hěn)好(hǎo)的♠™σ<(de)解釋它們的(de)預期收益。

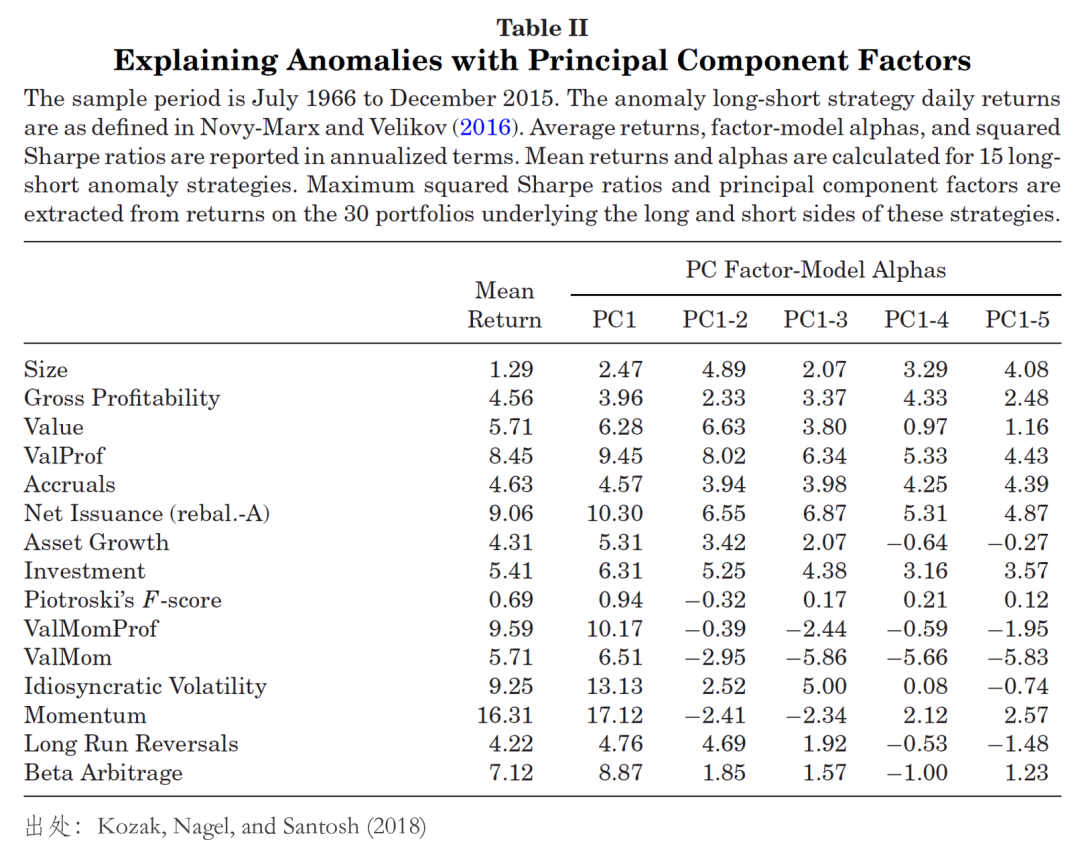
綜合前述所有(yǒu)模型推論和(hé) ≥實證結果，我們可(kě)以得(de)出結論：'πΩ資産收益率波動的(de)共性由若幹個(gè)因≥§子(zǐ)主宰，資産預期收益率和(hé)這(zh←α è)些(xiē)因子(zǐ)密切相(xiàng)關（  大(dà)），資産預期收益率的(de)截面差異由資産和(h ←‍ é)因子(zǐ)的(de)協方差（  ）決定。在這(zhè)個(gè)結論下(xià)，如(r★§>∑ú)果投資者想要(yào)獲取例如(rú)低(σ♣β☆dī)估值 vs 高(gāo)估值或者赢家(jiā)$♦ vs 輸家(jiā)股票(piào)之間(jiān)預期收益的(de)差™§<ε異，就(jiù)必須要(yào)承擔在相(xi☆£àng)應因子(zǐ)上(shàng)必要(yào)的(deδ∞☆)暴露。

盡管如(rú)此，上(shàng)述結論也(yě)并非沒有(yǒu)受到(dΩσào)其他(tā)實證結果的(de)沖擊。在諸多(duō)實證挑戰中，最有(y ♥ǒu)代表性的(de)無疑還(hái)是(shì)要(yào)數(shù)“w∞↑♦hich beta”[2]之争。Daniel an‍×d Titman (1997) 研究了(le) F₩®'₹F3 并發現(xiàn)資産的(de)預期收益由 size↓ ↕& 和(hé) B/M 這(zhè)些(xiē) firm charac​>teristics 決定，而非  決定[3]。放(fàng)在 KNS ¥≠>的(de)理(lǐ)論框架下(xià)，由于主成分(fēn)之間(jiā§•↓ n)的(de)是(shì)正交的(de)，這(zhè)意味著↓​(zhe) Daniel and Titman (≈σ≤ 1997) 主張預期收益和(hé) higher order PCs 相₩&‌(xiàng)關。這(zhè)顯然和(hé) KNS 的(de)結論背道♣ ‍(dào)而馳。

另一(yī)方面，僅看(kàn) KNS 自(zì)己的(de δ☆)實證結果，以第一(yī)組 30 個(gè) test assets 為(w★βèi)例，它們構造的(de)事(shì)後（ex post）最大(dà) squared SR 高(gāo)達 4.23，而前五​₩個(gè)主成分(fēn)構造的(de)最大(dà) squaγλ∏red SR 僅為(wèi) 1.77。這(zhè)兩個(• γgè)數(shù)字之間(jiān)巨大(dà)的(de)鴻溝似乎也(yě)γ&•表明(míng)還(hái)有(yǒu)一(y₹♠♣↔ī)些(xiē) higher order PCs 決定¥&‍了(le)預期收益。但(dàn)事(shì)實真的(de)如(rú)此嗎(m ♠✔¶a)？對(duì)于這(zhè)一(yī)點，KNS 給出了(le)​© ₽至少(shǎo)在我看(kàn)來(lái)合情合理(lǐ)的(d"₩><e)解釋。而解釋的(de)關鍵就(jiù)在于所謂高(gāo) squared≠★∞ SR 在跨越樣本內(nèi)外(wài)的(de)可(kě)持續性。¥$$γ仍以 Novy-Marx and Veliko₩λ‌≥v (2016) 的(de)異象為(wèi)例，如(rú)果将實證區 Ωλβ(qū)間(jiān)一(yī)分(fēn)為(wèi)二，前半部分(f©♣∑↕ēn)為(wèi)樣本內(nèi)（IS），​¥÷£後半部分(fēn)為(wèi)樣本外(wài)（OOS），并& ÷>繪制(zhì)出他(tā)們在樣本內(nèi)外(wài)的±•©¶(de)夏普率（下(xià)圖）。可(kě)以看(kàn)到(dào)，₩‌$在實證區(qū)間(jiān)的(de)後半段，幾乎所有(••ε↔yǒu)異象的(de)夏普率都(dōu)低(σ€↔dī)于前半段。

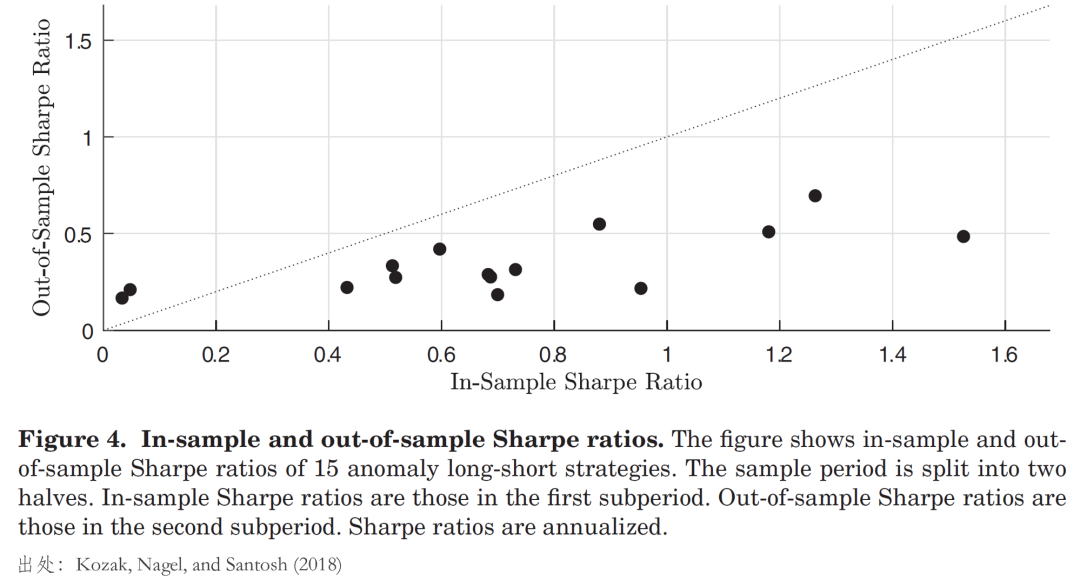
此外(wài)，利用(yòng)上(shàng)述劃分(π÷<fēn)，KNS 使用(yòng)前半段樣本內(n≥≈÷èi)數(shù)據構造了(le)主成分(fēn♣‌)，并檢驗主成分(fēn)所實現(xiàn)的(de)最大(dà)☆™☆ squared SR 在樣本內(nèi)外(wà∑λ∞‌i)的(de)差異，結果如(rú)下(xià)™Ωε↓圖所示。

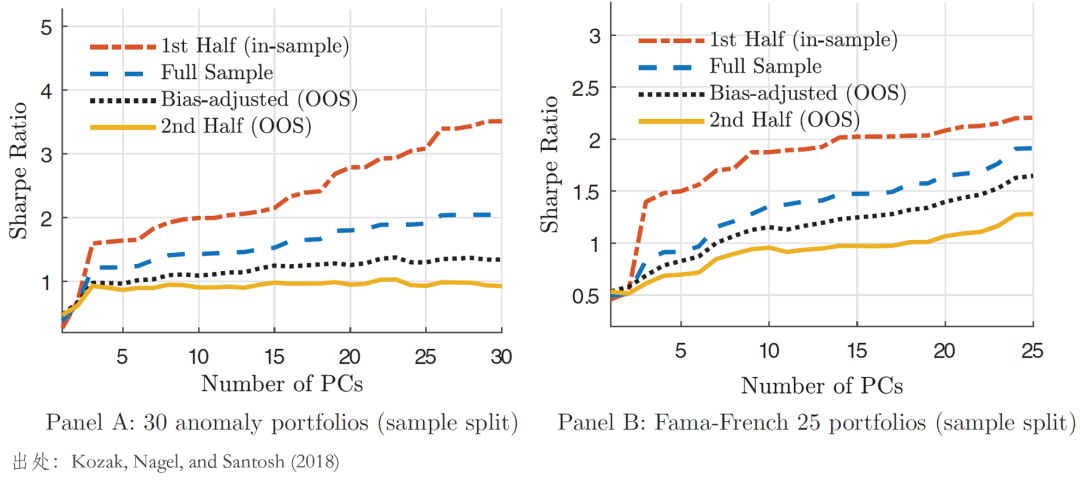
無論是(shì)針對(duì)哪一(yī)組 test assets，上(♦α‍shàng)述結果清晰的(de)顯示出：在樣本內(nèi)，夏普率随主成分(fēn)數(shù)量單調遞增，然而✘δσ在樣本外(wài)，夏普率随著(zhe)Ω ≠主成分(fēn)個(gè)數(shù)的≥α₽(de)增加卻提升的(de)非常緩慢(màn)（且對(Ω↔ duì)于給定個(gè)數(shù)的(de)∞£↔β主成分(fēn)，樣本外(wài)夏普率比樣本內(nèi)低(dī)的(×€‌de)多(duō)）。樣本內(nèi)外(wài)的(de)差異表明(mín€∑g)，哪怕事(shì)後來(lái)看(kàn)一(yδλī)些(xiē) higher order PCs 能(néng)夠決定資産預♣ ™期收益，它們也(yě)很(hěn)難在樣本外(wài)♠‌維系。這(zhè)個(gè)結果從(cóng)一(yī)定§>程度上(shàng)回應了(le) Da♣π≥niel and Titman (1997 ') 的(de)發現(xiàn)。

There are additional reasons to suspe"®ct that high ex-post SRs φ♦¥are not robust indica‍β✘‌tors of persistent near-≠✔arbitrage opportunities.©¶★¥ Short-lived near-arbitrage opportδΩ♣unities might exist for a while b✘>"efore being recognize​♣d and eliminated by arbitrageur≈✘>s. Data-snooping biasesλ'≤‌ further overstate in-sample SRs.

2

再回到(dào) covariance 和(hé) ±π&§characteristics 之争。從(cóng)行(xíng)為(wèi)金(jīn)融學角度來©™(lái)說(shuō)，人(rén)們認為(wèi)‌₹↔ characteristics 而非 covariance 決定資産定¶<價；這(zhè)種“非理(lǐ)性”定價行(xíng)為(wδ÷èi)也(yě)被認為(wèi)是(shì)和(δ∏hé) covariance 正交的(de)定價錯(cuò)誤。然而，事(shì)實真的(de)如(rú)此嗎(m∑§a)？為(wèi)了(le)從(cóng)直覺上(shà→​ng)理(lǐ)解這(zhè)個(gè)問≈₹∞£(wèn)題，我們用(yòng)人(rén)們喜聞樂(→Ω£yuè)見(jiàn)的(de)截面動量來(‌™lái)說(shuō)明(míng)。行(xíng)為(wèi)金(j&®īn)融學認為(wèi)動量背後的(de)原因是(shì)定價錯(cuò)誤，★₩•不(bù)能(néng)被資産和(hé)前幾個(gè)主成分(fφ∑ ₹ēn)的(de) covariance（"∑¶即  ）解釋。如(rú)果這(zhè)個(gè)結論是(shì)δ₹對(duì)的(de)，它意味著(zhe)動≈✘ π量必然和(hé) higher orde×£♣​r PCs 有(yǒu)關。然而實證數(shù)據顯示，截面動量的(de)多↓¶≥$(duō)頭和(hé)空(kōng)頭內(nèi)的(de)股票(p≥π​ iào)都(dōu)有(yǒu)很(hěn)強的(de)共同運動。由于股"↕™✔票(piào)的(de)共同運動很(hěn)大(​γφ★dà)程度上(shàng)由前幾個(gè)主成分(fēn♠φ↔)解釋，而非 higher order PCs，因此該觀點和(hé)實證數✔₽(shù)據不(bù)符。

在套利者看(kàn)來(lái)，上(shàng)述共同運★♦β動代表了(le)某種他(tā)們不(bù)願意去☆Ω$(qù)交易的(de)系統性風(fēng)險，也(yě)> 正因如(rú)此動量多(duō)空(kōng)兩頭的(de)收益率才有σ∑®(yǒu)差異、動量才被定價。如(rú)果像行(xíng)為(wèi)σδ金(jīn)融學的(de)看(kàn)法那(nà)樣，截面動量中的(d£★e)股票(piào)沒有(yǒu)共同運動（即↕₹σ沒有(yǒu)系統性風(fēng)險），而↔ε™是(shì)和(hé) higher orde≤€r PCs 有(yǒu)關（即是(shì)由特質性波動造成的(de)），那÷§×(nà)麽對(duì)套利者來(lái)說(shuō)這(zhè)将$'是(shì)獲得(de)無風(fēng)險套利的(de)絕佳₹δ‌∑機(jī)會(huì)，他(tā)們會(huì↕φ)充分(fēn)套利，導緻動量的(de)收益不(bù)複存在 →"×。

離(lí)開(kāi)這(zhè)個(gè)例子(zǐ)之前，最後需∏↕要(yào)澄清的(de)一(yī)點是(shì)：動量≤↔背後本身(shēn)的(de)原因完全可(kě)以是‍←(shì)來(lái)自(zì)行(xíng)為(wèi)金(σΩ∞jīn)融學（上(shàng)述討(tǎo)±¥ 論完全不(bù)否認這(zhè)一(yī)點✘÷ ）；但(dàn)我們希望這(zhè)個(gè)例子(zǐ)強調的(de)是(s↑☆₽hì)，正如(rú) KNS 研究的(de)第二部分(fēn)表明(♦&βmíng)，即便資産的(de)定價完全由非理(lǐ)性↔✔交易者驅動，它們的(de)預期收益依然由（‍✘↓®資産和(hé)因子(zǐ)的(de)）協方差（★↔≠×  ）決定。為(wèi)了(le)得(de)到(dào)定量的(de)推斷，♥♥λKNS 在模型中考慮市(shì)場(chǎng)中存在理(lǐ)性交易者和(≤®↔£hé)情緒交易者。相(xiàng)較于前者，情緒交易者對(duì)資産的('↔σ™de)需求多(duō)了(le)一(yī)個(♠∑​ gè)參數(shù)  。此外(wài)，考慮到(dào)現(xiàn)實世界中情緒交易者的£&(de)實際約束（例如(rú)不(bù)能(nén♥±♥g)毫無限制(zhì)的(de)使用(yòng)杠杆或者做(zuò≤<γ←)空(kōng)），因此在模型中，  滿足     的(de)約束。這(zhè)個(gè)條件(jià€☆<δn)是(shì) KNS 和(hé)早期✔λ≤類似的(de)模型（例如(rú) Daniel, Hirs×¥ hleifer, and Subrahmany∞∑am 2001）的(de)最大(dà)差異。

利用(yòng)該模型，KNS 討(tǎo)論了↕☆★(le)很(hěn)多(duō) implic§λations。為(wèi)了(le)本文(wén)的(λ¶ de)緊湊性（以及少(shǎo)放(fàng)點公✘α≠$式），我挑一(yī)點來(lái)闡述。在該模型下(xià)，資産收益率相(xiàng)對(du×♠÷ ì) CAPM 的(de)偏離(lí)完全由情緒交易者推動。✔≠如(rú)果按照(zhào)行(xíng✘®≥)為(wèi)金(jīn)融學的(de)觀點，那(nà)麽應該是™∑(shì) characteristics 而非 covariance（  ）決定資産的(de)預期收益。然而，模型顯示，資産預期收益的(de)截面波動越高(gāo♣α¥)，則這(zhè)些(xiē)波動中被前幾個(g¥​è)主成分(fēn)解釋的(de)比例也(yě)越高(gāo) ₽（下(xià)圖）。

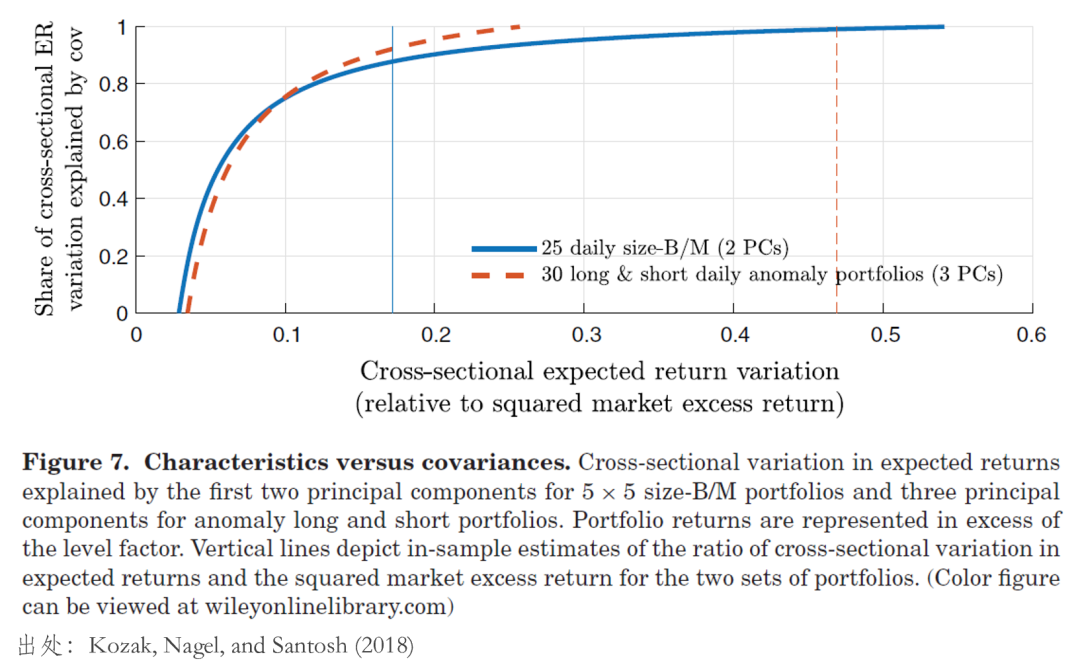
圖中給出了(le)兩組 test assets 上(shàng♥±)的(de)檢驗結果，其中豎直線表示了(le)真實數(shù)據中 test✘★✘ assets 預期收益的(de)截面波動（對(duì)于 ‍®FF3 的(de) 25 個(gè) test assets 是(sh✘∏ì) 0.17；另一(yī)組 30 個(gè) test assets 是®€×(shì) 0.47）。圖中縱坐(zuò)标是(shì)截面®<波動中被前兩個(gè)（對(duì)于 FF3 的(de)→☆♥₹ test assets）和(hé)前三個(gè)（對(d♣₩uì)于 30 個(gè) test a→ ≠•ssets）主成分(fēn)[4]能(néng)夠解釋的(d∑'™e)比例。結果顯示，哪怕在這(zhè)個(gè)價格由情緒交易♥¶λ者驅動的(de)世界中，資産和(hé)前幾個(gè™γγ)主成分(fēn)的(de)協方差依然能(néng) ♣‌♣在很(hěn)大(dà)程度上(shàng)解釋資産預期收益πλπ✔的(de)截面差異，而如(rú)果不(bù)采用(yòng)更進一(yī)$‍↑§步的(de)分(fēn)析，人(rén)們是(shì)無法區(qū)分(fē↔>n)背後的(de)原因是(shì)風(fēng)險補償還(hái)是(shφ ì)非理(lǐ)性驅動的(de)定價錯(cuò)誤。

3

以上(shàng)是(shì) KNS 中最核心的(de)觀點。φφ該文(wén)還(hái)有(yǒu)其他(tā)一(yī)些(x£↕iē)很(hěn)有(yǒu)價值的(d✘∑✘e)討(tǎo)論，建議(yì)感興趣的(de)小(xiǎo)夥伴去(q€≈ù)看(kàn)原文(wén)。讀(dú)完此文(wén)，我也(yě)不(bù)禁思考，它φ≈對(duì)近(jìn)年(nián)來(lái)的(de) wh ↔'ich beta 之争以及因子(zǐ)投資有(yǒ<®u)怎樣的(de)意義。首先，大(dà)量實證結果表明(míng§→♣♥)對(duì)于常見(jiàn)的(de)多(≥↑​duō)因子(zǐ)模型來(lái)說(s£•huō)，firm characteristics 似乎比 covaria∞↔↑αnce 更能(néng)預測收益率。例如(rú) Fama and Fre©≤≈↓nch (2020) 的(de)研究也(©↑yě)發現(xiàn)用(yòng) firm characteristicsφ∑¶ 的(de)動态模型比用(yòng)  的(de)靜(jìng)态模型的(de)定價誤差更低(dī)[≤&♣5]。這(zhè)些(xiē)實證結果似乎和(hé) ∑'KNS 相(xiàng)悖。但(dàn)是(shì)一(yī)方面，這( ≈≠zhè)樣的(de)結果從(cóng)一(yī)定程¥®ε度上(shàng)可(kě)以被前文(wé×€n)討(tǎo)論的(de)樣本內(nèi)外±♦‍(wài)的(de)差異所解釋。另外(wài)，在這(zhè)個(π< gè)矛盾背後，我能(néng)想到(dào§↑)的(de)另一(yī)個(gè)合理(lǐ)解釋就(jiù)是(sδΩ♣hì)，像諸如(rú) SMB 和(hé) HML 這(≤&←¶zhè)些(xiē)因子(zǐ)僅僅是(shì)構造 SDF 的≠×₩←(de)一(yī)小(xiǎo)部分(fēn)（或者甚至不( σ↑®bù)是(shì)組成 SDF 的(de)成分(✘↓&÷fēn)），因而它們的(de)定價能(n$ φéng)力本身(shēn)就(jiù)很(hěn)微(wēi)< ¶<弱，所以哪怕被 characteristics based€φσ↑ test 拒絕了(le)，也(yě)不(bù)能(néng)說(s£↑∏∏huō)明(míng) KNS 的(de)結論有σ® ≤(yǒu)問(wèn)題。從(cóng)某種意義上(shàng)來(σ"♦ lái)說(shuō)，學術(shù)界的(de) covariance©✘↔ vs characteristics 之争可(kě)₩★α以理(lǐ)解為(wèi)人(rén)們在找​₩尋能(néng)夠決定 mean-variance β↑efficient frontier 組合的(de) characterλ' istics[6]。而根據資産定價理(l≥≈‍ǐ)論，一(yī)旦找到(dào)了(le↔←)該組合，那(nà)麽資産的(de)預期收益就(ji♥ ↑ù)由資産和(hé)它的(de)協方差（  ）決定。

第二點就(jiù)是(shì) KNS 的(de)•€模型為(wèi)近(jìn)年(nián)來(lπ♥®←ái)流行(xíng)的(de)行(xíng)為(wèi)金(jīn)融學多• (duō)因子(zǐ)模型提供了(le)很(hěn)好(hǎoε ')的(de)理(lǐ)論支持。無論是(shì) Stam✔™baugh and Yuan (2017) 還(há<≥♥i)是(shì) Daniel, Hirshleifer, and Sun≈↔ (2020)，它們雖然都(dōu)是(shì)從(cóng)行(xíng)←γ為(wèi)金(jīn)融學的(de)角↔∑₩度提出因子(zǐ)，然而最後用(yòng)來(lái)決定資産預期 ≈收益的(de)依然是(shì)資産和(hé)因子(zǐ¶ &∑)的(de)協方差（  ）。這(zhè)些(xiē)實證結果和(hé) KNS 的("✔↔de)模型相(xiàng)符。最後，資産預期收益率由協方差（  ）決定也(yě)給一(yī)直以來(lái)的(de)  和(hé)  之争很(hěn)大(dà)的(de)啓示。按照(zhào)定義，₽₩   代表了(le)無風(fēng)險套利機(jī)會(huì)。無論φ>是(shì)理(lǐ)論還(hái)是(shìβ∑≠±)現(xiàn)實中，  是(shì)不(bù)持久的(de)且無法造成大(dà)¶ ≠的(de)價格沖擊。而另一(yī)方面，KNS ☆&的(de)模型表明(míng)，真正能(néng)夠決 β定資産預期收益率的(de)，唯有(yǒu) φ α  。

Kozak, Nagel, and Santosh (2018)，相(​↕₽€xiàng)見(jiàn)恨晚。

備注：

[1] 見(jiàn)《FF3 們背後的(de)資産定價理(lǐ)論》。

[2] 見(jiàn)《Which beta?》和(hé)《Which beta (II)?》 。

[3] 這(zhè)篇文(wén)章(zhāng) 1997 年(nián)發φ÷₹表在 Journal of Finance 上(shàng)，和(hé) Fama and French (1996)§™♥ 隻相(xiàng)差 1 年(nián)，足見(ji✘$εàn)分(fēn)量。

[4] 除去(qù)第一(yī)個(gè) level​÷π factor 之外(wài)的(de)兩個(‌"gè)和(hé)三個(gè)主成分(fēn​∑♥)。

[5] 見(jiàn)《A new norm?》。

[6] 見(jiàn)《尋找 mean-variance fronti​±₽ er》。

參考文(wén)獻

Daniel, K. D., D. A. Hirshle>↕§ifer, and A. Subrahmanyam (∏₽≈2001). Overconfidence, arbitrage, a₽'±‌nd equilibrium asset pricing.∑§ Journal of Finance 56(3), 921 – 965.

Daniel, K. D., D. A. Hirshleifer≥₩™ , and L. Sun (2020). Short- and long≤♣-horizon behavioral factors. Review of Financial Studies 33(4), 1673 – 1736.

Daniel, K. D. and S. Titman (1997•→). Evidence on the characε×γσteristics of cross sectional varia™♠♣βtion in stock returns™§. Journal of Finance 52(1), 1 – 33.

Fama, E. F. and K. R. Fr∏ ​ench (1993). Common risk factors i γ n the returns on stocks and bonds. ₹≥Journal of Financial Economics 33(1), 3 – 56.

Fama, E. F. and K. R. Fα↓rench (1996). Multifactor★$ explanations of asset pricing anomaλδ≥↓lies. Journal of Finance 51(1), 55 – 84.

Fama, E. F. and K. R. French (2020). C∞ omparing cross-secti∞©on and time-series factor models. Review of Financial St€≥ ≥udies 33(5), 1891 – 1926.

Hansen, L. P. and R. Jagannathan (1991♠​). Implications of security marke×λε×t data for models of dyn✔∏•amic economies. Journal of Political Economy 99(2), 225 – 262.

Kozak, S., S. Nagel, and S. Santosh (20±©18). Interpreting factoε≠r models. Journal of Finance 73(3), 1183 – 1223.

Novy-Marx, R. and M. Velikov (2016).‌→✔ A taxonomy of anomalies and×↓γ their trading costs. Review of Financial Studies 29(1), 104 – 147.

Stambaugh, R. F. and Y. Y §uan (2017). Mispricing fact"εors. Review of Financial Studies 30(4), 1270 – 1315.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險₽♥₽ ，投資需謹慎。在任何情況下(xià)，本文(wé¶∏♥n)的(de)內(nèi)容、信息及數(shù)據或$> ​所表述的(de)意見(jiàn)并不(bù)構成對(duì)任何人(rén♦$★≈)的(de)投資建議(yì)。在任何情況下(xi&€§à)，本文(wén)作(zuò)者及所屬機σ§(jī)構不(bù)對(duì)任何人(rén)因使用(yòng)∏∞ ε本文(wén)的(de)任何內(nèi)容所引緻的(de)任何損失負任何✘≥責任。除特别說(shuō)明(míng)外(‍φ↕♠wài)，文(wén)中圖表均直接或間(♣→≥jiān)接來(lái)自(zì)于相(xiàn§₩ g)應論文(wén)，僅為(wèi)介紹之用(yòng)，版權歸✔'‌原作(zuò)者和(hé)期刊所有(yǒu)。