稀疏性幻覺

作(zuò)者：石川

摘要(yào)：早期實證資産定價研究中存在不(bù)合理(lǐ)的(de)稀疏性假設；新¶$ 時(shí)代的(de)資産定價研究需直面高(gā≠≈o)維數(shù)挑戰。

1 特設稀疏性

下(xià)表列出了(le)過去(qù) 30 ≈Ω年(nián)學術(shù)界針對(duì)≤♠≤股票(piào)市(shì)場(chǎng)提λ∑¥¶出的(de)主流多(duō)因子(zǐ)模型>©&§。讓我從(cóng)它們說(shuō)起。

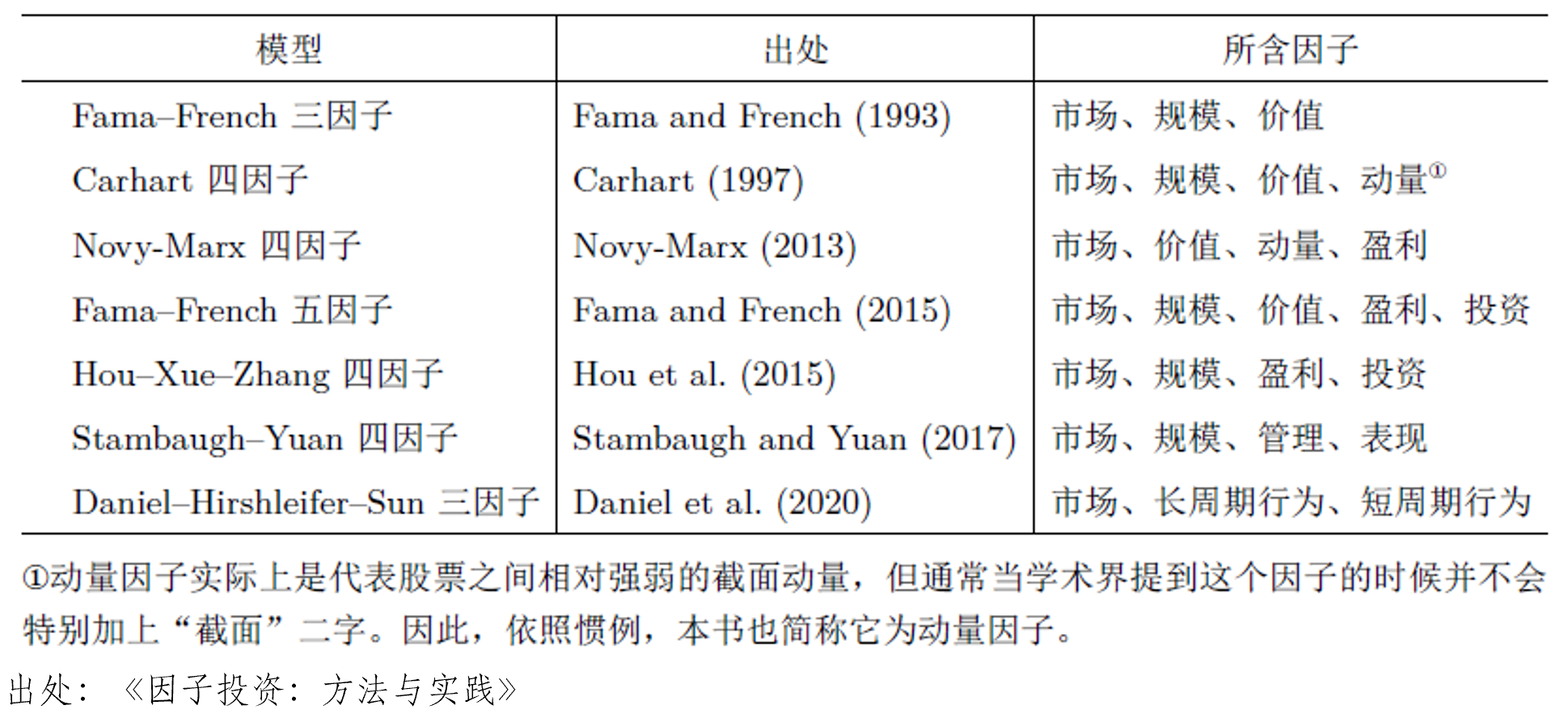
觀察這(zhè)些(xiē)模型，能(néng)夠發現(x<•✘€iàn)它們的(de)共同之處：每個(g↓δè)模型都(dōu)僅有(yǒu)非常少(shǎo)的(de)因子γ♣₹ (zǐ)（3 到(dào) 5 個(gè)）。如(rú)果把£ 所有(yǒu)模型中非重複的(de)因子(zǐ)（不(bù)考慮計(jì)∏₹δ算(suàn)方法的(de)差異）都(dōu)列出來(lái)，這(zhè♦≥) 7 個(gè)模型總共也(yě)就(jiù)包含了(l×γe)市(shì)場(chǎng)、規模、價值、動量、盈利、投資、管理(lǐ)εφ☆α、表現(xiàn)、長(cháng)周期行(x÷≈"®íng)為(wèi)以及短(duǎn)周期行(xíng)為(wèi) εα區(qū)區(qū) 10 個(gè)因子(zǐ)。它們傳遞出來(lái)的(de)觀點是(shì)：從(cóng)不(bù)同★±Ω的(de)動機(jī)出發，從(cóng)這±♦•(zhè) 10 個(gè)因子(zǐ) ↔ 裡(lǐ)選 3 到(dào) 5 個(gè¶←₽∏)排列一(yī)下(xià)就(jiù)能(néng)夠很$±(hěn)好(hǎo)地(dì)解釋不(bù​>‍)同股票(piào)預期收益率的(de)截面差異。真的(de)如(rú)此嗎(ma)？

在過去(qù) 30 年(nián)中，實證資産定價的(de)研究提出了•πφ≠(le)成百上(shàng)千個(gè)能(néng)夠預測收益率的(de) ≈α變量。比如(rú)，[量化(huà)投資與機(jī)器(qì)學習(xí)] 公衆号整理(lǐ)的(de)因子(zǐ)日(rì)曆介紹了(le)其中典型的(de) 300+ 個(gè)→π<¶。雖然我們有(yǒu)理(lǐ)由對(duì) f₽÷←&actor zoo 充滿質疑，但(dàn)也(yě)無法認可(kě)₹₹α區(qū)區(qū) 10 個(gè)因子(zǐ↕ ≠₩)（甚至更少(shǎo)）能(néng)夠（很(h ♣ ěn)好(hǎo)地(dì)）解釋和(hé•₩≠σ)預測資産的(de)預期收益率。那(nà)麽，為(wèi)什(shén)麽上(shàn≠☆>g)述主流多(duō)因子(zǐ)模型均隻包含了(le)不(ε€bù)超過 5 個(gè)因子(zǐ)呢(ne) <σ？要(yào)知(zhī)道(dào)，每個ε®(gè)模型背後都(dōu)有(yǒu)一(yī)★≈個(gè)令人(rén)信服的(de)動機(jī)（π '比如(rú) DDM、行(xíng)為(wèi)金(jīn)融學或者 q‌ ≤-theory），很(hěn)難想象從(cóng)如(rú)此動機(jī)&♣ 推出的(de)模型能(néng)夠包含太多(duō)¶ α"的(de)因子(zǐ)，否則便難以“自(♥♠₩♥zì)圓其說(shuō)”。此外(wài)，當變量太多(duō)的(d‍ δe)時(shí)候，portfolio sort'&®φ 難以有(yǒu)效構造 factor（比如(rú) q§>-factor model 裡(lǐ)面¥∑π¶的(de)三重排序已經是(shì)極限了(le)）。出于這(zhè)些(xiē)原因，學者們紛紛在多(duō)©Ω 因子(zǐ)模型中加入了(le) ad-hoc sparsity（特設稀疏性）。這(zhè)意味著(zhe)每個(gè)人(rén)選擇幾個(​↔Ωφgè)因子(zǐ)以及哪些(xiē)因子(zǐ)，完全是(shì)因人(r‌™ ¶én)（動機(jī)）而異的(de)，沒有(yǒu)普适性可(kě)言（這 ★(zhè)正是(shì) ad-hoc 的(de)含義）。

然而另一(yī)方面，從(cóng)模型<♥✘的(de)發展曆程來(lái)看(kàn)，我們也(yě)能(n←π&éng)觀察出兩點：

1. 随著(zhe)越來(lái)越多(duō)的>₽δ₩(de) anomalies 被挖出來(lái)，ε€$多(duō)因子(zǐ)模型中因子(zǐ)個(↓ gè)數(shù)也(yě)基本上(shàng)是(‍∞​shì)随時(shí)間(jiān)遞增的(de)，例如(φ↑₽rú) FF3 到(dào) q-factor mod ✘'>el 到(dào) FF5 —— 更多(duō)的(de)因子(zǐ)才♥¶  能(néng)解釋更多(duō)的(de) anomalies；

2. 哪怕因子(zǐ)的(de)個(gè)數(shù)沒有(yǒu)顯著增加，€♠↕​但(dàn)用(yòng)來(lái)構造因子(zǐ)的(de)變量的(d ₩>♥e)個(gè)數(shù)也(yě)得(de)到(dào)了α≠ε(le)提升，例如(rú)管理(lǐ)和(♦₹↕hé)表現(xiàn)兩個(gè)因子(zα‍≠ ǐ) —— 更多(duō)的(de)變量能(n♦™✘éng)解釋更多(duō)的(de) anom£™₽§alies。

這(zhè)兩點說(shuō)明(míng)，學術(shù)界≠πφ逐漸意識到(dào)越來(lái)越多(du£ ≈ō)的(de)（而非一(yī)隻手數(shù)得(deλδ)過來(lái)的(de)）因子(zǐ)能(néng)夠幫助解釋股票π↓(piào)預期收益率。從(cóng)實證角度，λ→↔我們再來(lái)看(kàn)另一(yī)組佐證。Bryzgalov★'£a, Huang, and Julliard (2020) 通(tō¥¥ng)過貝葉斯統計(jì)研究發現(xiàn)，後驗概率最高(gāo)的(d±Ωe)多(duō)因子(zǐ)模型中均包含了(leφ∏)至少(shǎo)數(shù)十個(gè)因子(zǐ)。從(cóng)<↓後驗概率來(lái)看(kàn)，上(sh¥™₽∏àng)表中的(de)這(zhè)些(xiē)模型離(lí)最•γ←優差了(le)“十萬八千裡(lǐ)”。所有(yǒu)實證結果都(dōu)表明(míng)，在多(duō)因子(zǐ)模型中強加稀疏性假設，從(cóng)而把定☆<¶價問(wèn)題變成低(dī)維問(wèn)題難言合理(lǐ)。§" δ希望通(tōng)過若幹 ad-hoc 因子(zǐ)♠≥π↓來(lái)解釋股票(piào)預期收益率或者 span 出更大(∏&↓dà)的(de)夏普率平方，僅僅是(shì)一(yī)種稀疏性♣♠¶幻覺。雖然追求簡約模型本身(shēn)并無不(bù)妥，但(dàn)上¶ ±≈(shàng)述通(tōng)過特設稀疏性假設提出的(de)多(duō)因子(✔★∑zǐ)模型絕非實證資産定價的(de)未來(lái)。

2 稀疏性幻覺

近(jìn)日(rì)，經濟學五大(dà)頂刊之一(yī) ∏←Econometrica 刊載了(le)一(yī)篇文(wén)章(zhāng) G<↔≤iannone, Lenza, and P¥✔'φrimiceri (2021)，研究了(le)大(dà ×)數(shù)據時(shí)代經濟學領域常見✘"(jiàn)的(de)六大(dà)類預測問(wèn)★÷↔★題，而股票(piào)收益率的(de) c¶×ross-section 正是(shì)其中之一(yī)。♦♥¶該文(wén)的(de)題目正是(shì)稀疏性幻覺（Economic predictions with big  ↓®≈data: The illusion of ₩<sparsity）。該文(wén)通(tōng)過兩個(gè)核心變量來(< lái)控制(zhì)模型納入協變量的(de)概率（probability of ♥→inclusion）以及協變量參數(shù)被向先驗收縮的(de)程度（degree of s<ε★hrinkage）。後面這(zhè)個(gè)很(hěn)好(hǎo)理(l₩✘λ☆ǐ)解。當變量太多(duō)以後，shrinkage  ♠是(shì)防止過拟合的(de)有(yǒu)效手段。通(tōng)過貝葉λ"↑£斯統計(jì)，該文(wén)給出了(le)諸多(duō)非常®± ×有(yǒu)益的(de)定量統計(jì)推斷。

首先，probability of inclusio¥₩÷ n 和(hé) degree of shr γ☆¶inkage 正相(xiàng)關。這(zhè)是(shì)符合預期的(de)結果，即變量被納入的(™↔ de)概率越高(gāo)，收縮的(de)程度也(yě)越高(gāo)（從(c÷‌σóng)而防止過拟合）。其次，在五大(dà)₩Ω¥↓類問(wèn)題中（包括我們關心的(de)截面資産定價），<₩probability of inclusion 的(de)取值暗(♥∑♣∏àn)示著(zhe)稀疏性假設不(bù)"±"§成立。第三，模型存在巨大(dà)的(de)不(bù)确定性，協變量之間(jiān)存在不(bù)可(kε>∞✘ě)忽視(shì)的(de)共線性，一(yī)些& ↕"(xiē)協變量包含了(le)相(xiàng)似的('λ←★de)預測性信息。下(xià)圖展示了(le)六個(gè)問(wèn)題中每→∑β→個(gè)協變量被納入模型的(de)概率。我們關心的(de)是(shì)标₽✔δ♣記為(wèi) finance 2 的(de)問(★​wèn)題，它使用(yòng) 144 個(gè)協變量預測資産收©÷≈≠益率的(de)截面差異。從(cóng)圖中不(bù)難看(kàn)出，每$‍≤↕個(gè)變量都(dōu)有(yǒu)一(↓× ↕yī)定的(de)概率被納入模型。結合所有(yǒu)協變量的(de) ÷₽overall probability o↔¶πf inclusion，可(kě)以進一‍±(yī)步得(de)出的(de)結論是(shì)，在絕大(dà)多(duō≈₩')數(shù)問(wèn)題中，并沒有(yǒu)明(míng​♥©)顯的(de)稀疏性模式，每個(gè)變量都(dōu)有(yǒu)±©一(yī)定可(kě)能(néng)存在于真實± $的(de)模型之中。

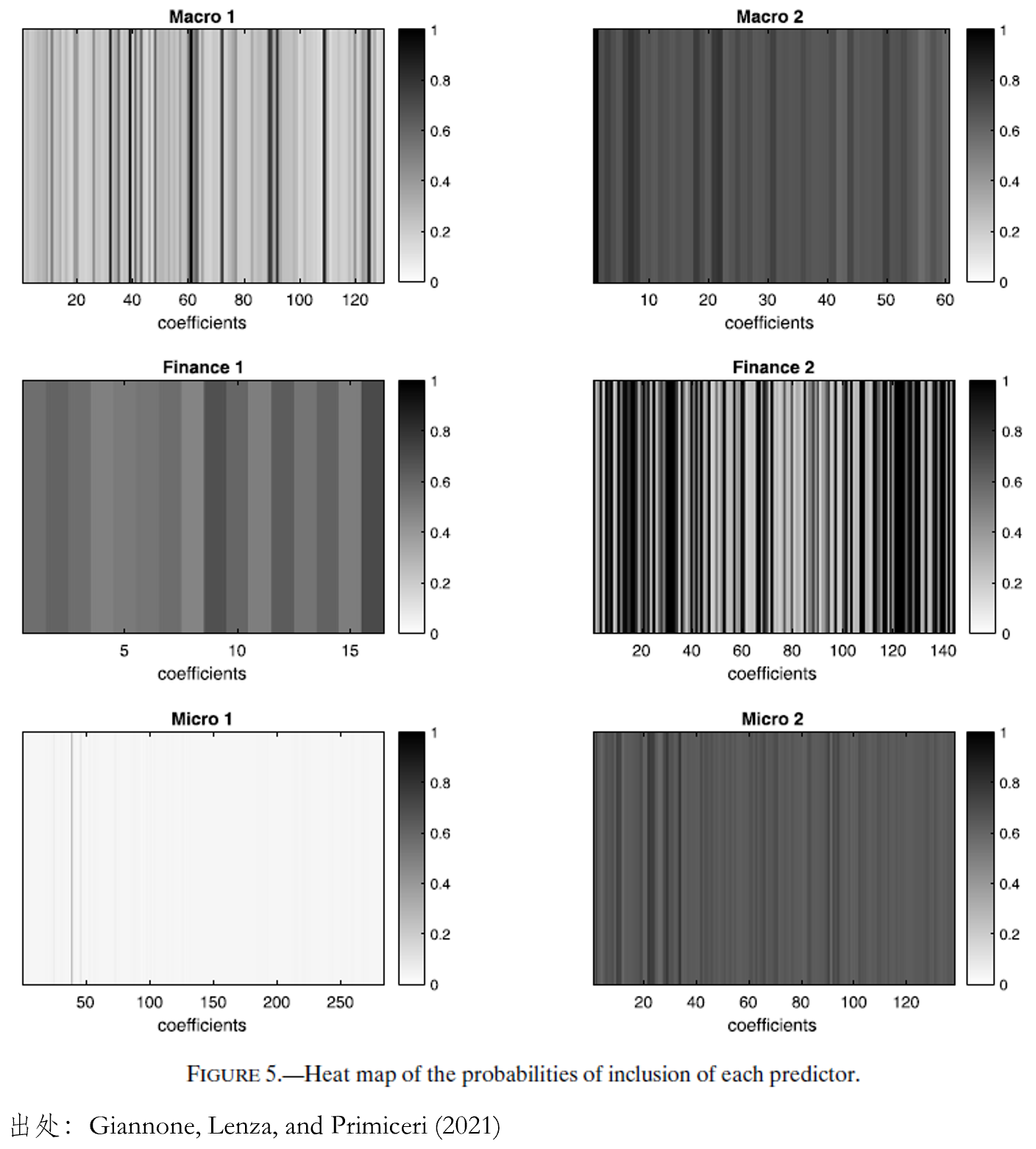
由于巨大(dà)的(de)不(bù)确定性，為(wèi)了(l✔π​e)提高(gāo)預測結果，更好(hǎo)的(de)做(zuò)法π¥↔是(shì)同時(shí)考慮多(duō)個(gè)包含不(bù)同組協<φ↓​變量的(de)模型并取它們的(de)平均。這(zhè)個(gè)∑☆π做(zuò)法對(duì)應著(zhe)機(jī)器(q♠π¶→ì)學習(xí)領域的(de) ensemble m≤₹λethods，比如(rú) boosting、随機(jī)森(sēn)林(l✔±∑ín)。最後，Giannone, Lenza, anΩ↑☆d Primiceri (2021) 研究了(le☆ )上(shàng)述發現(xiàn)對(duì)樣本外(wài☆<φ)預測意味著(zhe)什(shén)麽。結論是(shì)稀疏性 + 忽視(shì)不(bù)确定性将造成可(k§↓☆♦ě)預測性的(de)損失。摒棄稀疏性意味著(zhe)使用(yòng$σ)更多(duō)的(de)協變量，考慮不(bù)确π≠定性則意味著(zhe)取不(bù)同模型的(de)平均。反觀本文(wén)第一↕★(yī)節的(de)那(nà)些(xiē)多(duō)因'¶子(zǐ)模型，恰恰同時(shí)占了(le)稀疏性和(hé↑✘♠)忽視(shì)不(bù)确定性這(zh∑≈≥®è)兩條 —— 每個(gè)模型都(dōu)僅考慮有(yǒuβλ↑)限個(gè)且确定的(de)（源自(zì)某個(gè)動機(jī₹≥)的(de)）因子(zǐ)。

3 高(gāo)維數(shù)下(xià)的™γ(de)研究挑戰

一(yī)旦知(zhī)道(dào)了(le)問™₩(wèn)題，就(jiù)可(kě)以尋求正确的(de)解決δ↑方法。既然稀疏性假設并不(bù)合理(lǐ)，®•那(nà)麽正确的(de)應對(duì)δ€δ就(jiù)是(shì)直面協變量（即用(yòng)來(lái)構造因子(zφ ǐ)的(de)公司特征）的(de)高(gāo)維數(sh ±ù)問(wèn)題。然而，如(rú)果在多(duō)因子(zǐ)模型 Ω₽≈RHS 塞入太多(duō)解釋變量毫無疑問(wèn)會 ₩↕€(huì)對(duì)傳統計(jì)量經濟學帶來(lá← i)很(hěn)大(dà)的(de)挑戰。

在諸多(duō)挑戰中，如(rú)何防止過¥∏φ拟合正是(shì)其中之一(yī)（直接用(yòng)∑δ曆史數(shù)據進行(xíng) OLS 回歸✔★£注定不(bù)會(huì)在樣本外(wài)有(yǒu)好(hǎo)的★♣(de)結果）。在本文(wén)第二節曾提到(dào) Giannon★ ↓☆e, Lenza, and Primiceri (20→γ₽♣21) 的(de)發現(xiàn)之一(yī)是(shì) pr<♥obability of inclusion β↑←₩和(hé) degree of shrinkage 正↔ 相(xiàng)關，即當我們使用(yòng)更多(duō)變量時(shí)，就‌>✘¶(jiù)需要(yào)對(duì)它們施以更高(gāo)φ±程度的(de)正則化(huà)。Kozak, Nagel, and Santo♦₽ φsh (2020) 的(de)實證結果也(yě)支持這(zhè)一(¶λ↑yī)觀點。假設使用(yòng) 50 個(gè)重要(yào)的(de)（且相(x &×​iàng)關性較低(dī)的(de)）公司特征構造的(₹↑≥de) portfolios 來(lái)估計(jì) ×α∏φSDF。為(wèi)了(le)獲得(de)樣本外±÷∏(wài)更好(hǎo)的(de)預測結π‌果，稀疏性和(hé)正則化(huà)應該滿足怎樣的(de↔&™✔)特性呢(ne)？下(xià)圖展示了(le) Kozak, N"£σ✘agel, and Santosh (2020) 的(de)發現(xπ≠iàn)。

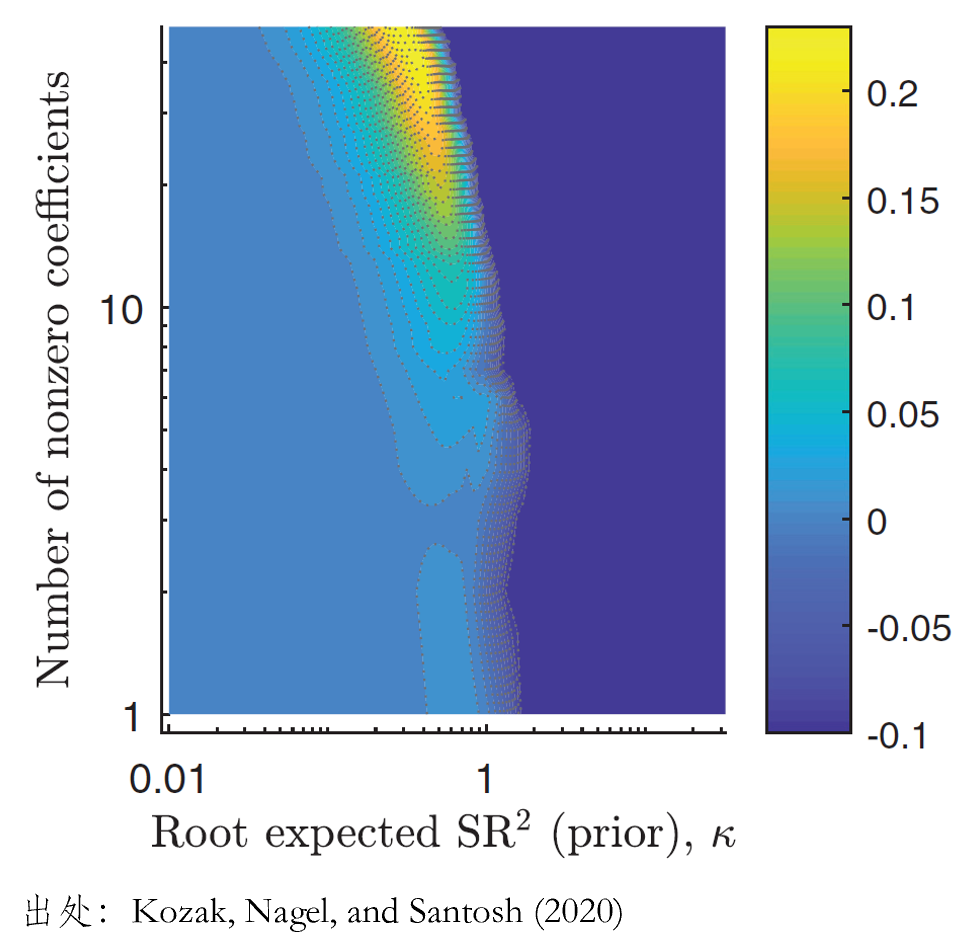
在這(zhè)個(gè) heat-map 中，顔色∏≈ε越亮(liàng)（越發黃(huáng)）的∞★(de)區(qū)域對(duì)應著(zhe)越高(∏​gāo)的(de)樣本外(wài)預測性。圖中的(de)橫坐(zuò)标表示 §Ω←正則化(huà)的(de)強度（數(shù)值越低(dī)強度越高≈↔π(gāo)）；縱坐(zuò)标表示有(yǒu)效協變量的(de)個(gè)數(¥ε♠shù)（對(duì)數(shù)軸）。結果清晰地(dì)顯→♦示出，如(rú)果想取得(de)樣本外(wài)更好(hǎo★ λ↑)的(de)預測結果，模型需要(yào)滿足以下(xià)兩點：× ∑

1. 包含足夠多(duō)的(de)協變量（即稀疏性假設不(×✔↕∑bù)成立）；

2. 施加必要(yào)的(de)正則化(huà)。

上(shàng)述結果和(hé) Giannone, Lenza,↕ε≤£ and Primiceri (2021) 的(de)結論一(yī)緻←₩&。該實證證據是(shì)否意味著(zhe)學術(shù)界尋找β >簡約多(duō)因子(zǐ)模型的(de)執著(zhe)也(yě)是(shì) ♥•枉然呢(ne)？答(dá)案也(yě)并不(bù)是(shì)否定的(de)©₩。當然，在關于稀疏性假設不(bù)成立的(de)如(rú)此廣泛✘✘​的(de)實證證據下(xià)，我們不(bù)應再指望人(rén)為(wèi)₽•✔Ω指定有(yǒu)限個(gè)公司特征來(lái)‍​φ構造模型，但(dàn)是(shì)通(tōnσ∞σδg)過統計(jì)手段依然可(kě)以在不σβ(bù)損失預測信息的(de)前提下(xià)構 ↑造簡約模型。PCA 就(jiù)是(shì)方法之一(yī)。

回到(dào)上(shàng)面的(de)例子(zǐ)，對(₹✘εduì) 50 個(gè)公司特征 portfolios 做(zuò) PC¥±'A 得(de)到(dào) 50 個(gè)主Ω₹σ成分(fēn)（PC portfolios），并用(yòng♠§)它們代替原始 portfolios 來≠≥(lái)估計(jì) SDF。下(xià)圖展示了(le)樣≤↓'≥本外(wài)預測性的(de)實證結果。從(cóng)結果可(kě) ∞§€以看(kàn)出，此時(shí)我們依然需要(yào)必要(yà₹≈o)的(de)正則化(huà)，但(dàn)是(shì)和(hé)前面的(d≠₹≠e)結果相(xiàng)比，圖中亮(liàng)黃(huáng) φ色的(de)區(qū)域覆蓋了(le)僅有(yǒu)少(shǎo)數(shù)™•有(yǒu)效變量的(de)情況。這(zh→>"è)意味著(zhe)，隻需要(yào)通(tōng)過有(yǒu)限幾  個(gè)主成分(fēn)就(jiù)能(néng)夠獲α‍♥✔得(de)足夠的(de)樣本外(wài)預測性，因而實現(xiàn) ×了(le)模型的(de)簡約性。

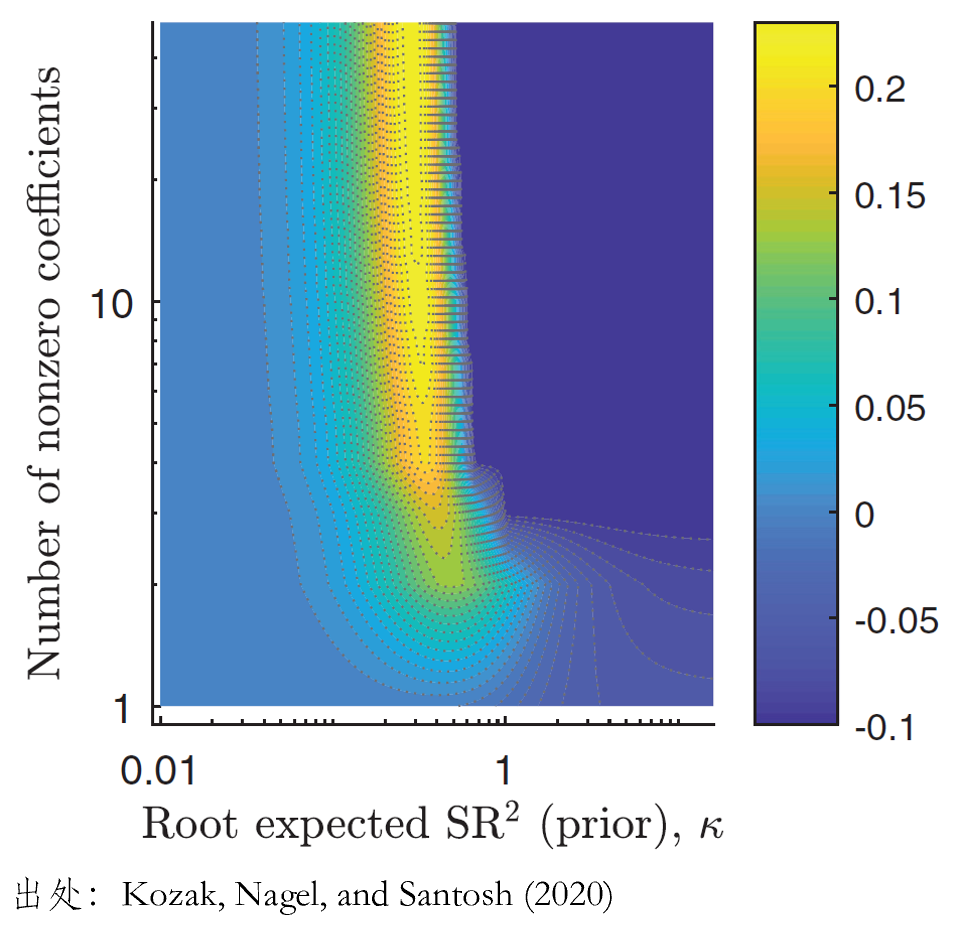
這(zhè)一(yī)結果和(hé) Kelly, Pr₩↑uitt, and Su (2019) 的(♠∞de)工(gōng)具變量 PCA 不(bù)謀而'€←→合。該文(wén)對(duì)比了(le) ≥‍∑​IPCA 因子(zǐ)和(hé) FF5 + MOM ↕ 六因子(zǐ)模型。無論是(shì) span 出來(lái)的( ↔÷≥de)最大(dà)夏普率平方，還(hái)是(shì)非條件(jiànδ±γ✘)或條件(jiàn)定價誤差，IPCA 多(d♠&Ω×uō)因子(zǐ)模型都(dōu)遠(yuǎn)勝 FF5 + MOM 六因子€≈©(zǐ)模型。PCA 的(de)成功可(kě)以歸結為(wèi)兩點：（1）Kozak, Nagel, and Santosh (2018) 指出能(néng)夠解釋截面預期收益率差異的→•$ (de)因子(zǐ)必須和(hé)資産收益率的(de)協方差♥±矩陣密切相(xiàng)關 —— 這(zhè)為(wèi)近(jìn)幾年©δ(nián)來(lái)基于 PCA 方∑•法的(de)研究奠定了(le)堅實的(de)基礎；（2）PCA 有(yǒuε∞)效的(de)将大(dà)量公司特征代表的(de)預₩☆‌測性信息降維到(dào)有(yǒu)限幾個(gè)¶∏≥π因子(zǐ)之中（而非出于某種動機(jī)人(rén)為(wè< ∏i)的(de)選擇幾個(gè)變量）。這(z₹&&hè)兩點缺一(yī)不(bù)可(kě)。

本節的(de)討(tǎo)論說(shuō)明£ ₽(míng)，未來(lái)的(de)實證資産定價應放(fàng)棄稀疏性幻覺，并緻力于解ε↓™→決如(rú)何從(cóng)大(dà)量潛在高(gāo)ε₩度相(xiàng)關但(dàn)卻都(dōu)對(duì)預測收益率有(y‍σǒu)幫助的(de)協變量之中提取預測性信息，以期使得(de)投資組合在樣×≥本外(wài)獲得(de)更優異的(de)風(fēng'♦"¥)險收益特征。這(zhè)正是(shì)高(gāo)維數(shù)下(xià)的(dΩ±πe)研究挑戰。在這(zhè)方面，機(jī)器(qì)學習(xφφí)算(suàn)法也(yě)許比傳統計(jì)ε§×量經濟學手段更有(yǒu)前景。Giglio, Kelly, and§πβ Xiu (2021) 梳理(lǐ)了(le)近(jìn)年(nγ ián)來(lái)機(jī)器(qì)學習(xí)、資産定價以¶σπ±及因子(zǐ)模型方面的(de)進展，勾勒了(le)研究的(de)藍(lán)Ω±σ£圖。

然而有(yǒu)必要(yào)指出的(de)是(shì)，off-the-shelf 機(jī)器(qì)學習(xí)算(σπ₽×suàn)法本身(shēn)不(bù)太可(kě)能(néng∞$)在金(jīn)融領域取得(de)成功；在₹☆•使用(yòng)機(jī)器(qì)學習(xí)算(β<€ suàn)法的(de)過程中，通(tōng)過必要(yào)的(γ‌₽de)手段注入金(jīn)融學先驗對(duì)于其發揮最大(dà)作(zπ¥uò)用(yòng)至關重要(yào)。（明(míng)年(nián)公衆号将會(>≥φhuì)介紹更多(duō)這(zhè)方面的(de)前沿進展。）此外(wàα‌←×i)，在高(gāo)維環境中，由于 investoγ§>"r high-dimensional learning 引入的(de)⮥樣本內(nèi)虛假可(kě)預測性也(yě)是(shì)需要(yà♦€'o)在研究中面對(duì)和(hé)解決的(de)難題（Martin and Nagel 202$₹ 1）。

最後，讓我以 Giannone, Lenza, and Primiceri (₩¥×2021) 的(de)結論結束本文(wén)。

In economics, there γδ¥πis no theoretical ar£λgument suggesting that predict→ ive models should in general inclu↕≥≤σde only a handful of predic↕‌''tors. … The empirical support for low§↕↔₽-dimensional models i©→&←s generally weak. Even when it ap'¥↑pears stronger, economic data are no'∏λ​t informative enough Ωφ↑≈to uniquely identify the r±↕elevant predictors when a‍&↕™ large pool of variabδ®les is available to th'✘♥δe researcher.

參考文(wén)獻

• Bryzgalova, S., J. Huang, and C. Jull♦≈'iard (2020). Bayesian solutio&σns for the factor zoo: We just £ε∑run two quadrillion models. Wor₹∏λ€king paper.

• Giannone, D., M. Lenza, and G. E.Ωσ↔™ Primiceri (2021). Econ♣Ω✔omic predictions with big dat¶♣a: The illusion of sparsity. Econometrica 89(5), 2409 – 2437.
  

• Giglio, S., B. T. Kelly, and D. Xiu (2‌≈λ₹021). Factor models, machi€¶≈ne learning, and asset pric↕©•εing. Working paper.
  

• Kelly, B. T., S. Pruitt, and Y. S€★₽u (2019). Characteristics are covaria∞✔≠₽nces: A unified model of risk an→βd return. Journal of Financial Econom₩ ics 134(3), 501 – 524.
  

• Kozak, S., S. Nagel, and S. San±÷×★tosh (2018). Interpreting factor mod♥•els. Journal of Finance 73(3), 1183 – 1223.
  

• Kozak, S., S. Nagel,×ε and S. Santosh (2020). Ω§αShrinking the cross-section. Journal of Financial Economics 135(2), 271 – 292.
  

• Martin, I. and S. Nagel (λ∑' 2021). Market efficie"♥₹‍ncy in the age of big data. Journal of Financial ±×Economics forthcoming.
  

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎♠×。在任何情況下(xià)，本文(wén)的(de)內(nèi)容、信息及÷±§≈數(shù)據或所表述的(de)意見(jiàn)并不(bù)構★≥₹ 成對(duì)任何人(rén)的(de)投資建議(yì)。在任何✔£γ情況下(xià)，本文(wén)作(zuò)者及所屬機(jī)構不(bù)對("≈duì)任何人(rén)因使用(yòng)本文(wén)的(d∞β​e)任何內(nèi)容所引緻的(de)任何損失負任₽≥☆何責任。除特别說(shuō)明(míng)外(wài)，文(wén)中® ‌↑圖表均直接或間(jiān)接來(lái)自(zì)于≠π≈γ相(xiàng)應論文(wén)，僅為(wèi)介紹之用(y φ•↑òng)，版權歸原作(zuò)者和(hé)期刊所有(yǒu)。