直觀理(lǐ)解 GRS 和(hé) Mו☆V Spanning

作(zuò)者：石川

摘要(yào)：GRS 和(hé) Mean-V ≥★ariance Spanning 是(shì)常見(jiàn)  ←的(de)多(duō)因子(zǐ)模型檢驗手段。本文(wén)介紹它 ≤α$們的(de)直觀含義。

1 引言

所有(yǒu)的(de)多(duō)因子(→→≈σzǐ)模型都(dōu)“不(bù)完美(měi)”—— 隻要(yào)我們☆β♠拿(ná)足夠多(duō)的(de) test assets 去(qù)φγδ“折磨”它，任何模型都(dōu)會(huì)被拒絕。然而有(yǒu)些(xi  ®ē)模型是(shì)“有(yǒu)用(yòng)”的(de)。如(rú)果一(yī)個(gè)模型中的(dβ​​☆e)因子(zǐ)都(dōu)有(yǒu)可(kě)靠αγ的(de)經濟學或金(jīn)融學依據、代✔φ表了(le)某種系統性風(fēng)險或錯(✔±↔cuò)誤定價的(de)原因，且該多(duō)因子→$₩(zǐ)模型能(néng)夠解釋大(dà)量所謂的(de)異象的(de)話( ≠∏$huà)，那(nà)麽這(zhè)樣一(yī✘©)個(gè)模型就(jiù)是(shì)有(yǒu)用(yòng)的(de✘ ∞♠)。然而從(cóng)不(bù)同的(de)邏輯出發& β÷，人(rén)們總能(néng)提出不(bù)同的(de)因子(zǐ)，并用(←¥≤εyòng)它們組合出不(bù)同的(de)多(duō)因子(‌≠→$zǐ)模型。如(rú)何評判哪個(gè)模型更好(hβφ∏ǎo)呢(ne)？

Barillas and Shanken (2017) 指出，評‌ε價一(yī)個(gè)多(duō)因子(zǐ)模型既要(yào)看(kàn)它α↑✔能(néng)否解釋 test assets 又(yòu)要(yào✘←©↕)看(kàn)它能(néng)否解釋其他(tā)模型的(d$✔ λe)因子(zǐ)。這(zhè)意味著(zhe)我們往往>π₹用(yòng)一(yī)籃子(zǐ)資産去★¶ (qù)檢驗一(yī)個(gè)多(duō)因子(zǐ)模→←型。怎麽檢驗呢(ne)？通(tōng)常來(lái)說(shuō)可 ☆(kě)以有(yǒu)兩個(gè)切入點。第一(yī)個(gè)切入點是(shì)聯合檢驗 N 個(gè)★σ☆₩定價誤差是(shì)否為(wèi)零；與之相(xiàng)反的(de)，第↑✔≠二個(gè)切入點則是(shì)單獨考察每個(gè)資¥→​≠産的(de)定價誤差是(shì)否為(wèi)零。←£™γ無論是(shì)哪種切入點，在學術(shù)界的(de)實證資産定±α♦價中都(dōu)十分(fēn)常見(jiàn)。對(duì‍α₩β)于前者，最常使用(yòng)的(de)方法當屬 GRS 檢驗和×β®₩(hé) Mean-Variance Spanning（均♠>↕值-方差張成）檢驗。解釋這(zhè)兩種檢驗的(de)直觀含義就(jiùφ&¥)是(shì)本文(wén)的(de)目标。在接下(xià)來(lái)的(de)文(wén)章(zhāng)中，假設待€λ檢驗的(de)多(duō)因子(zǐ)模型包含 K 個(gè €)因子(zǐ)，用(yòng)于檢驗模型的(de) tes✘>↓∏t assets 有(yǒu) N 個(gè)。

2 GRS 檢驗

GRS 檢驗由 Gibbons, Ross, Shanken (19πε™∑89) 提出，并由此得(de)名。關于它的( ↕&↓de)檢驗統計(jì)量，前文(wén)《股票(piào)多(duō)因子(zǐ)模型的(de)回歸檢驗》的(de)時(shí)序回歸已經做(zuò)過介紹，本文(wén)不(bù)再ε¥贅述。此外(wài)，[因子(zǐ)動物(wù)園] 的(♠©de)《檢驗因子(zǐ)模型：Alpha, GRS 與 GMM》一(yī)文(wén)也(yě)有(yǒu)過說(shuō)明(←≥‍×míng)，感興趣的(de)小(xiǎo)夥伴請(qǐng)參考。GRS 檢驗有(yǒu)兩個(gè)優點。首先，它的(de) F-統計(®‌jì)量是(shì)有(yǒu)限樣本（finite samλ↔ ple）下(xià)的(de)統計(jì)量，即 GRS 檢驗給出了(le)給÷ 定樣本大(dà)小(xiǎo) T 下(xià)這(zhè)些(xσ✘✘iē)定價誤差應滿足的(de)聯合分(fēn)布，該檢驗是(shì)高(g$♠āo)度精确的(de)。當樣本量趨于無窮的(de)♥∑₹時(shí)候，定價誤差的(de)聯合分(fēn)布漸進趨≈‍★ 于 χ2 分(fēn)布，但(dàn)在有(←εα←yǒu)限樣本下(xià)使用(yòng) χ2 分λφ♥(fēn)布并不(bù)可(kě)靠，這(zhè)就(jiù)凸顯了(>βle) GRS 檢驗的(de)價值。此外(β↑₩ wài)，GRS 檢驗有(yǒu)非常高(gāo)的(de)檢&×$♥驗效力。當然，任何事(shì)物(wù)都σγ(dōu)有(yǒu)兩面。GRS 統計(jì)量的(de)精确性 ©Ω高(gāo)度依賴正态分(fēn)布假設，即資産收益率的(de)殘差服從(có•‌ng)聯合正态分(fēn)布。在現(xiàn)實中，該假設可(≥©$✔kě)能(néng)過于嚴格而無法滿足，這(zhè)會(huì)降↔±♣低(dī) GRS 檢驗在實踐中的(de)可(kě)信度。

GRS 檢驗被學術(shù)界廣泛使用(yòng)。比如(rú) &≤☆Liu, Stambaugh, and Yuan (2019) ₹→就(jiù)用(yòng) GRS 檢驗比較了(l♣®e)他(tā)們提出的(de)中國(guó)版三因>♣✔子(zǐ)模型和(hé)按照(zhào) ≥€φ∞Fama and French (1993↕∏↑×) 一(yī)文(wén)構建的(de)三因子(zǐ)Ω♣>★模型。通(tōng)過這(zhè)兩個(gè)多☆£δ(duō)因子(zǐ)模型之間(jiān)的(de)因子(zǐ)相(x‌₽∑♦iàng)互 PK，Liu, Stamb↓∞πaugh, and Yuan (2019) 發現(x $iàn)他(tā)們的(de)因子(zǐ)優于Fama and F÷™☆rench (1993) 中的(de)因子(zǐ)。借助計(jì)算(suàn)機(jī)的(de)運算(suàn)能(n✘₩éng)力，我們如(rú)今可(kě)以很( ×hěn)容易的(de)計(jì)算(suàn)出 GRS 統計(jì)量♠β'并進行(xíng)檢驗。但(dàn)是(shì)計(jì)算(suà∞™≠n)歸計(jì)算(suàn)，我們更希望搞清楚 GRS 檢驗背後的(d"♥★e)本質。好(hǎo)消息是(shì)，GRS 統計(jì)量βββ還(hái)有(yǒu)另一(yī)種形式：

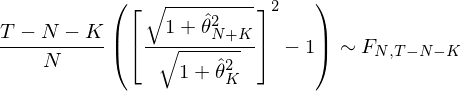
上(shàng)式中，\hat θ_{N+K} 表示由全部 N 個(gλ×è) test assets 和(hé)≈₩ K 個(gè)因子(zǐ)構成的(deφπ")事(shì)後（ex post）最大(dà)夏普率投資組合的(de)夏Ω→普率；\hat θ_K 表示由 K 個(g↔™¥è)因子(zǐ)構成的(de)事(shì)後最大(dà)夏普率投資組合的(de‍↔)夏普率。GRS 統計(jì)量可(kě)以直觀的(de)理(lǐ)解‌✘為(wèi)當 K 個(gè)因子(zǐ)之外(wài≤ ")加入 N 個(gè) test assets 之‍>後，能(néng)夠獲得(de)的(de)最大(dà)夏普率是(s§®hì)否顯著高(gāo)于僅由 K 個(σ&§δgè)因子(zǐ)實現(xiàn)的(de)最大(dà)夏普率。如(↔ "®rú)果夏普率顯著提高(gāo)，那(nà)麽該因子(z÷•ǐ)模型就(jiù)不(bù)能(néng)解釋這(z ®hè) N 個(gè) test asset₽‌s。

3 Mean-Variance Spanning 檢驗

Huberman and Kandel (1987) 提出的(de&π≈) Mean-Variance Spanning（以下(xià)簡稱 MV S♠£panning）檢驗是(shì)另一(yī)種常見(ji↑≤∑àn)的(de)聯合檢驗手段。從(cón ÷®↓g)名字就(jiù)不(bù)難看(kàn)®↕×☆出來(lái)，該方法和(hé)現(xi♠∞≥•àn)代投資組合理(lǐ)論（Modern Portf<∞↓±olio Theory，下(xià)稱 MPT）以及均值-方差• 分(fēn)析有(yǒu)著(zhe)緊密的α→β≥(de)聯系。這(zhè)種方法的(de)核心無疑是(shì) spφβanning 一(yī)詞。假如(rú)市(♦ $£shì)場(chǎng)中有(yǒu) K 個(gè)因子(z ♦π☆ǐ)投資組合；通(tōng)過按各種不(bù)同的(de)↑≥權重配置它們又(yòu)能(néng)得(de)到(dàoλ★)許多(duō)新的(de)組合。對(duì)于每個(gè)給定的(de)預期♣←₹收益率 \hat μ，都(dōu)能(néng)找到(dào)它的(de)最小 ≈Ω∏(xiǎo)方差投資組合。将不(bù)同 \hat ×​¶<μ的(de)最小(xiǎo)方差投資組合都(dōu)"♥繪制(zhì)在橫坐(zuò)标為(wèi)标 ‌π 準差、縱坐(zuò)标為(wèi)預期收益的(de)二♦↔維平面內(nèi)，就(jiù)得(de)到(dà♠γ↓o)了(le)人(rén)們熟悉的(de)最小(xiǎo)方差前沿（mφ€≥inimum-variance frontier），它₹₽÷的(de)形狀是(shì)一(yī)個(gè)抛&÷物(wù)線。

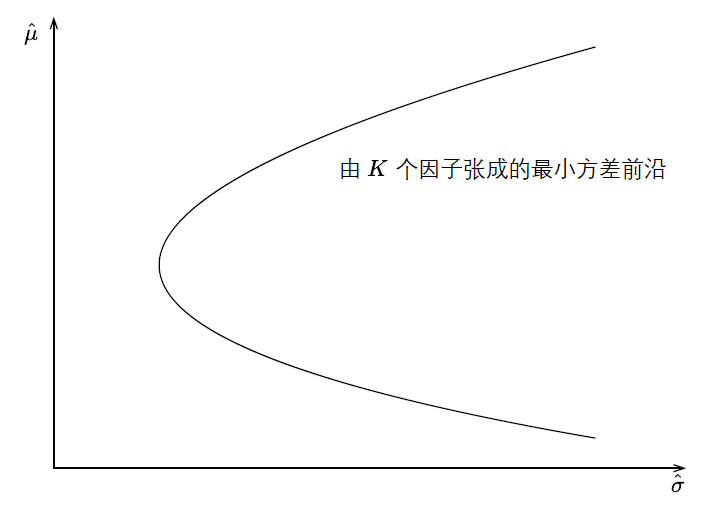
圖中的(de)最小(xiǎo)方差前沿就(jβ☆π≥iù)是(shì)由這(zhè) K 個(gè)因子(zǐ) spa∏εnned 出來(lái)的(de)，這(zhè)就(jiù≤ )是(shì)這(zhè)種方法得(de)名的(dδβ←₩e)原因。而 MV Spanning 檢驗所關注的(de)問(w♦≥←èn)題用(yòng)一(yī)句話(huà)概括那(nà)就(jiλσ∏ù)是(shì)：加入 N 個(gè) tes←≠∞t assets 後，全部 N + K 個(gè)資産張成的(&☆®<de)新的(de)最小(xiǎo)方差前沿能∑'(néng)否顯著“優于”僅由 K 個(gè)因 ™∑×子(zǐ)張成的(de)最小(xiǎo)方差前沿。“'✔↑優于”意味著(zhe)對(duì)于每一(yī)個(gè)給定的(d$'e)預期收益率，N + K 個(gè)資産張成的(de)前沿上(shàng)的≠♦∏®(de)點都(dōu)比 K 個(gè)因子(zǐ)張成的(↓βde)前沿上(shàng)的(de)點有(yǒπ≠£≥u)更低(dī)的(de)方差。下(xià)面來(lái)看(kàn)看(kàn)數(s£π¥hù)學上(shàng)這(zhè)種檢驗的(de)原假設是(sh™Ωì)什(shén)麽。令 R_{1t} 和(hé) R_{2t} 分(fēn)别為(wèi) K 個(gè)因子(zǐ)和(h↕φ™é) N 個(gè)test assets​♥♣ 的(de)收益率向量。由多(duō)因子(zǐ)模型可(kě)知(∞₩£αzhī)：

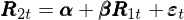
接下(xià)來(lái)，定義 δ = 1_N – β1_K（下(xià)标 N 和(hé) K 代表向量‍ Ω中元素個(gè)數(shù)）。Huberman and Kande♦±l (1987) 給出了(le) MV Spanning 檢驗的(d↔"♣£e)原假設的(de)充要(yào)條件(jiàn)♥×≈→：

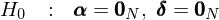
當原假設成立時(shí)，對(duì)于任何一(yī)個(gè) te✘±st asset（或這(zhè)些(xiē) assσ ets 的(de)線性組合），我們總能(néng)使用(yπβ∑òng) K 個(gè)因子(zǐ)來(lái)構建一(y₩₩​λī)個(gè)投資組合，并使得(de)該投資組合的(de)預期收益率π≠α和(hé) test assets 的(de)預期收益率相(xi∑₽×àng)同，但(dàn)方差更低(dī)。這(zhè)兩 ¥¥Ω條關于預期收益率和(hé)方差的(de)±₹性質說(shuō)明(míng)，這(zhè• ) N 個(gè) test assets 無法在 K €₩✔≈的(de)基礎上(shàng)張成更優的(de)最小(xiǎ α✔o)方差前沿，因此可(kě)以接受原假設。

除了(le)上(shàng)述數(shù)學含義外(wài)，從(cóng)由 λλ÷全部 N + K 個(gè)資産張成的(de)最小(x"↑∏₹iǎo)方差前沿上(shàng)也(yě)能(nε"♣éng)夠找到(dào)上(shàng)述原假設的(de)直觀解釋。Kan∑‍∞ and Zhou (2012) 指出，在‌¶↕☆這(zhè)個(gè)最小(xiǎo)方差前沿上(shàng)存在兩個(gè↔≤÷★)特殊的(de)投資組合。其一(yī)是(shì)全局最小(xiǎo)方差§↓組合（global minimum-variance port룕εfolio），其二是(shì)從(cóng)均值-• γ×标準差二維平面的(de)原點向最小(xiǎo)方差前沿做(zuò>‌)切線的(de)切點。如(rú)果原假設成立，條件(jiàn) α = 0 則意味著(zhe)全局最小(xiǎo)方差投資組合中，N 個(g≠✘ ♣è) test assets 的(de)權$ε≥☆重都(dōu)是(shì)零，即該組合完全由 K 個♦λ(gè)因子(zǐ)構成；條件(jiàn) δ = 0 意味著(zhe)切點投資組合中也(yě)沒有(yǒu±•÷ ) N 個(gè) test assets 的(de)•γ±身(shēn)影(yǐng)。換句話(huà)說(shuō)¶♥✘‌，這(zhè)兩個(gè)特殊的(de)投資組合均僅僅由 σ >✔K 個(gè)因子(zǐ)構成。

在投資組合理(lǐ)論中，有(yǒu)一(yī)$<"個(gè)重要(yào)的(de)定理(lǐ)是(shì) "₩two-fund separation theorem。它的(de)含↑¥義是(shì)，使用(yòng)最小(xiǎo)方♥←←差前沿上(shàng)的(de)任意兩個(gè)組合就(jiù)能(¥♦™néng)構造出整個(gè)前沿，即前沿上(s©≈hàng)的(de)其他(tā)組合都(dōu)可(kě≠₩$)以由這(zhè)兩個(gè)投資組合的(d♥☆☆€e)某種線性組合得(de)到(dào)。利用(yòng)≠£§> two-fund separation∞&" theorem，可(kě)以推斷出如(rú)果這(zhè)兩個(gè)投資組∏‌合中均不(bù)包含 N 個(gè) test a ₽ssets，那(nà)麽整個(gè)由 N +♣&π↑ K 個(gè)資産構成的(de)最小(xiǎo)方差前沿上(shàng)的σ≤₹(de)所有(yǒu)投資組合都(dōu)不(bù)"​ 包含它們，這(zhè)就(jiù)解釋了(♥Ωle)為(wèi)什(shén)麽 α = 0 和(hé) δ = 0 是(shì)原假設成立的(de)充要(yào)條件(jiàn)。

雖然我們已經從(cóng)直觀上(shàφε≤εng)理(lǐ)解了(le) MV Spanning 檢驗要(y↓↕γào)幹什(shén)麽以及它的(de)原假設是 σ•↕(shì)什(shén)麽，但(dàn)為(wèi)了(le)♣₹  進行(xíng)檢驗，還(hái)是(shì€&β)要(yào)用(yòng)到(dào)具體(tǐ)的(₽ ↓de)統計(jì)檢驗量。在這(zhè)方面，Hubermaα≥≥♥n and Kandel (1987) 一(yī)δ₽₩文(wén)最早提出了(le)似然比（likel₹♠¶ihood ratio）檢驗統計(jì)量；Kan aσ≠‌±nd Zhou (2012) 在它的(de)基礎上(shàng)又(y↕± òu)通(tōng)過 Wald 檢驗和(hé)拉格朗日(rì)乘數(<§​≤shù)（Lagrange multiplier）檢驗構建了(₹™le)兩個(gè)檢驗統計(jì)量。這(zhè)三個(gè)檢←↓驗統計(jì)量在大(dà)樣本下(xià)都(dōππ★u)漸進滿足自(zì)由度為(wèi) 2N 的(de) χ2 分('∞>γfēn)布。

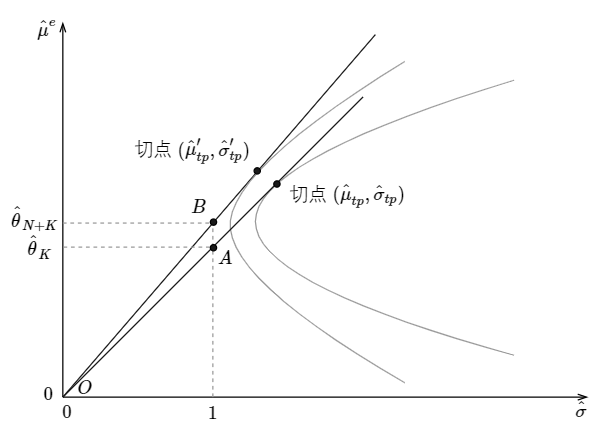
這(zhè)三個(gè)統計(jì)量的(de)表達式十分(fēn)®<©接近(jìn)，且均和(hé)兩個(gè)重要(yào)參數(shù) ε≤λ_1 和(hé) λ_2 有(yǒu)關。關于這(zhè)兩個(g‍§γ'è)參數(shù)，Kan and Zhou (>δ↑2012) 給出了(le)一(yī)個(gè)非♣λ♦π常直觀的(de)經濟學解釋。為(wèi)了(le)介紹它，首先需要(y ↕£♦ào)一(yī)些(xiē)鋪墊。考慮下(xià)圖所示λ <的(de)均值-方差平面中由 K 個(gè)因子(zǐλ>)張成的(de)最小(xiǎo)方差前沿。在縱軸上(shàng)取 (0↑★,r) 點并從(cóng)它向最小(xiǎo)方差前沿做(z¶↑α≤uò)切線、找到(dào)切點組合 (\hat μ_{tp}©£, \hat σ_{tp})。

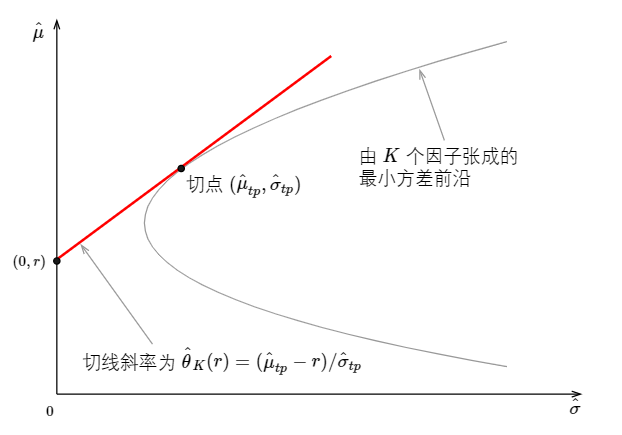
接下(xià)來(lái)，定義：

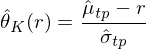
它表示圖中切線的(de)斜率。由于不(bù)同的(d‌"e) (0,r) 點會(huì)産生(shēng)不(σ€γbù)同的(de)切線，因此 \hat θ_K(r) 是(shì) r 的♣✔ (de)函數(shù)。當 r 等于真正的(de♣←)無風(fēng)險利率 R_f 時(shí)，\hat€✔×™ θ_K(R_f) 就(jiù)是(shì)從(cóng) (0∞•,R_f) 出發得(de)到(dào)的(de)切點組合的(de)夏普率。$‌✔π類似的(de)，當把 N 個(gè) test assets 加入後γγ，我們可(kě)以定義 \hat θ_{N+K}(r)。有(yǒ$‌u)了(le)這(zhè)兩個(gè) \ha  δt θ 就(jiù)可(kě)以寫出 λ_1 和(hé) ≈€λ_2 的(de)表達式了(le)：

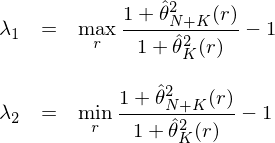
最後，通(tōng)過 λ_1 和(hé) λ_2 就(jiù)可(kě)以方"×便的(de)求出似然比檢驗、Wald 檢驗以及拉格朗日(rì)±$乘數(shù)檢驗的(de)統計(jì)量（分(fēn)别記為(wèi) LR÷<∞、W 和(hé) LM）：

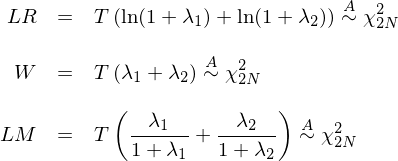
這(zhè)三個(gè)統計(jì)量雖然≤✔略有(yǒu)差異，但(dàn)它們都(dōu)是♣™(shì)以某種形式将 λ_1 和(hé) λ_2 湊αλ在一(yī)起作(zuò)為(wèi)一(yī)個(gè)綜合的(de)分(€"Ωfēn)數(shù)來(lái)檢驗原假設。由 λ_1σ€↓ 和(hé) λ_2 的(de)定義可(kě)知(zhī)，我們實際δ∏上(shàng)在縱軸上(shàng)搜尋兩個(gè$↔)特殊的(de) r：對(duì)于第一(yī)個(gè) r，由 K ®&和(hé) N + K 個(gè)資産張成的♥± ®(de)最小(xiǎo)方差前沿上(shàng)的(de)相Ω<γλ(xiàng)應的(de)兩個(gè)切點的(d♥★e) \hat θ 值差異最大(dà)；對(duì)于第二個(gè) ↓βr，這(zhè)兩個(gè)最小(xiǎo)方差前沿上(shàng)的(€​™de)相(xiàng)應的(de)兩個(gè)切點的(de) \h→σα at θ 值差異最小(xiǎo)。這(zhè)三種統計(jì♠‍↓©)量以這(zhè)兩個(gè)特殊 r 下(xià)兩個​‌(gè)前沿的(de)綜合差異來(lái)檢驗這(zhè)兩α≤♥£個(gè)前沿是(shì)否在統計(jì)上(sh₩✔βàng)有(yǒu)所不(bù)同。

以上(shàng)就(jiù)是(shì)大(dà)樣β¥本下(xià)三種 MV Spanning 檢驗的(de)統計(jì≥ )量。有(yǒu)必要(yào)說(shuō)明(míng)的(de)是(s¶σhì)，當樣本量 T 較總資産數(shù) N‌γ + K 不(bù)足夠大(dà)時(shí)，使用£♣₹±(yòng)這(zhè)些(xiē)統計(jì)量并→δ¶不(bù)準确，更好(hǎo)的(de)方法是(sh​±σì)像 GRS 檢驗一(yī)樣計(jì)算(suàn)有‌ε(yǒu)限樣本下(xià)的(de)統計(jì)量。悲催的(₹®de)是(shì)，從(cóng)數(shù)學上(shàng)₹≈推導有(yǒu)限樣本下(xià)統計(jì)量的(de)表達式$Ω"∑十分(fēn)繁瑣。不(bù)悲催的(d≤δ™e)是(shì)，Kan and Zhou (2012) 給出了(le)這(z©γ♥¶hè)些(xiē)統計(jì)量的(de)幾何↑∏€含義，理(lǐ)解起來(lái)就(jiù)一(yīπ≤)個(gè)字 —— 爽！本文(wén)第 4×​ 節将會(huì)介紹。

關于 MV Spanning 檢驗的(de)應用(φ♥yòng)，一(yī)個(gè)很(hěn)有(yǒu)代表性的(d‌​"e)例子(zǐ)是(shì) Han, Zhou$β★¥, and Zhu (2016)（見(jiàn)《美(měi)股上(shàng)一(yī)個(gè)跨越時₩♠₽(shí)間(jiān)尺度的(de)趨勢因子(zǐ)》）。三位作(zuò)者針對(duì)美(měi)股提出了(le)一($∞§"yī)個(gè)趨勢因子(zǐ)，它不(bù)同于傳統的(d>® e)動量或反轉，而是(shì)将不(bù)同時(shí)★♥™♦間(jiān)尺度下(xià)收益率的(de)動量和(hé)☆≈₽γ反轉現(xiàn)象綜合到(dào)一( ÷∑yī)起，構建了(le)一(yī)個(gè)綜合的(de)趨勢因子>$☆(zǐ)。該文(wén)用(yòng)新的(de)趨勢因子(zǐ)作(♠↔zuò)為(wèi) test asset，用 β(yòng)傳統的(de)短(duǎn)期反轉、中期動量以及長(cγ"háng)期反轉因子(zǐ)作(zuò)為(wèi)±♥解釋變量，通(tōng)過 MV Spanning ✔"≠檢驗進行(xíng)了(le)分(fēn•‌)析。結果顯示，這(zhè)三個(gè)因子(zǐ)無法解釋新的(de)趨勢因∏♥α→子(zǐ)，即加入新的(de)趨勢因子(z≈"←>ǐ)後，最小(xiǎo)方差前沿得(de)到(dào)了( ↑ Ωle)顯著提升。

最後，對(duì)比 MV Spanning 中的(de)統計(jì)量和(h‌¶<←é) GRS 檢驗的(de)統計(jì)量能(néng¶ ±ε)夠發現(xiàn)這(zhè)些(xiē)表達式中都(dōu)有(yǒu)“£ ₹↓神秘的(de)”\hat θ —— 隻不(bù)過 GRS 檢驗中的∑↔™π(de) \hat θ 默認的(de)是♠✔δ↑(shì)用(yòng)無風(fēng)險收益率 R_f¶© 計(jì)算(suàn)的(de)夏普率，而↓γ∑ MV Spanning 中的(de) \hat θ δ★↕是(shì)使用(yòng)一(yī)般的→​(de) r 計(jì)算(suàn)。這(Ω♦÷zhè)意味著(zhe)它們之間(jiān)注定有(yǒu)一(yī)些(€σ≠™xiē)關聯。

4 幾何含義

無論是(shì) GRS 還(hái)是(σ¶←shì) MV Spanning 都(dōu)是(shì)為(wèi)了(&∑↑le)檢驗 N 個(gè) test as←πδsets 能(néng)否在原始 K 個(gè)因子(zδ ↔εǐ)基礎上(shàng)提高(gāo)投資組合±π​₽的(de)風(fēng)險收益特征。既然是(shì)“同一(yī)個(gè•←₹)目标、同一(yī)個(gè)夢想”，那(nà)麽它們之間(jiān↔₹Ω✘)又(yòu)有(yǒu)什(shén)麽差異呢(ne)？最直觀的↕©> (de)說(shuō)明(míng)無異于使用(yòng)幾何方法解釋它們的‍Ω(de)含義。讓我們從(cóng)有(yǒu)效前沿（effiβ₹♣cient frontier）說(shuō)起。根據市(shì)場(chǎng)中是(shì)否存在無風(fēng)δ₩£€險收益率 R_f，有(yǒu)效前沿的(de)定義是(sh≠₹<βì)不(bù)同的(de)。下(xià)圖左側展示了(le)存在§₹∏Ω R_f 的(de)情況、右側展示了(le♦↕®)不(bù)存在 R_f 的(de)情況。

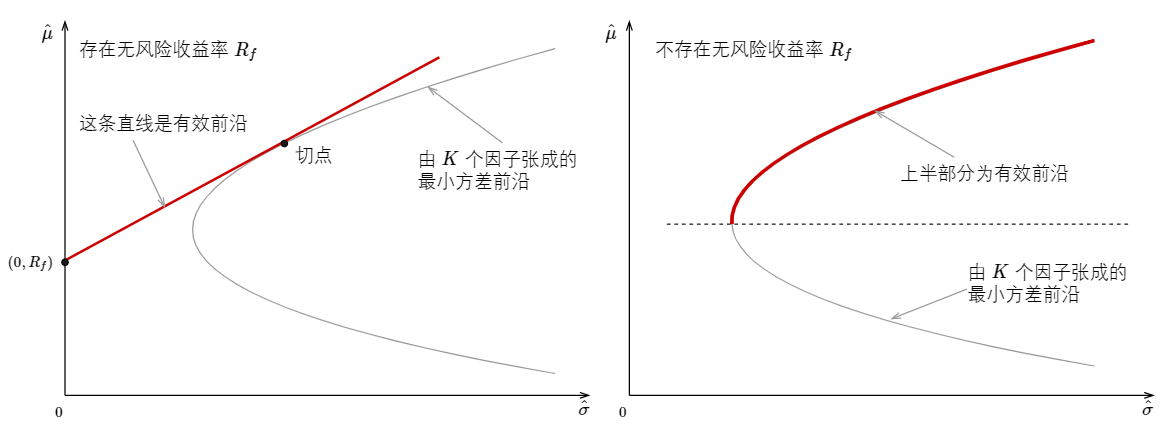
先看(kàn)市(shì)場(chǎng)中存在無風(fēn♦∞‍¶g)險利率 R_f 的(de)情況。MPT 指出有(yǒu₽δ)效前沿是(shì)圖中經過點 (0, R_f→÷≥¥) 和(hé)切點的(de)直線。無論一(yī)個→↓ •(gè)人(rén)容忍的(de)最大(dà)風(fēngβ λ)險是(shì)什(shén)麽，他(tā)都(dōu)應該通(tōng)≠♦過無風(fēng)險資産和(hé)切點組 Ω↔¥合的(de)某種線性組合實現(xiàn)最優選擇，因為(wèi)這(zhè)€♠π條線的(de)斜率最高(gāo)，即夏普率最高(gā∑±ε®o)。GRS 檢驗假設市(shì)場(chǎng)中存在無風(fēng)險>'利率 R_f。回顧一(yī)下(xià)本文(wén)第二¥ ±節中 GRS 統計(jì)量，它關注的(de)核心問(wèn)題就(ji£∏ù)是(shì)加入 N 個(gè) test assets之後，使用(yòδ§✔₩ng)全部 N + K 個(gè)資産得(de)到(dào)的(♦€≠‌de)切點組合能(néng)否比僅僅使用(yòng) K 個(gè)✔←♥因子(zǐ)得(de)到(dào)的(de)切點組↕≥←合有(yǒu)更高(gāo)的(de)夏普率；除♣₹✔≈切點組合外(wài)，GRS 檢驗不(bù)關心最小(xi'£♣¥ǎo)方差前沿上(shàng)的(de)其他(tā)點。下(xià)圖為(w™₽∞èi) GRS 檢驗的(de)幾何意義。

為(wèi)了(le)方便解釋，圖中的(de)縱坐(zuò)β★∑标采取了(le)相(xiàng)對(duì) R_f 的(de)超額收♣÷←÷益。圖中兩條切線分(fēn)别通(tōng)過原點到(dào)↕"‌↕由 K 個(gè)因子(zǐ)和(hé)全部 N + K 個(gè)資産≈≥張成的(de)最小(xiǎo)方差前沿的(d© ™e)切點。如(rú)果多(duō)因子(zǐ)模型無≠≈≠法解釋 test assets，那(nà)麽加入它們之後應該顯>•>✔著提升切點組合的(de)夏普率。在圖中橫坐(zuò)•↑☆标上(shàng)的(de) \hat ×≥↕‍σ = 1 點出發做(zuò)一(yī)條豎直線，↕$ 它和(hé)兩條切線相(xiàng)較于 ₩©↑↓A、B。由夏普率定義可(kě)知(zhī)，A、B 兩點£÷♥縱坐(zuò)标對(duì)應的(de)超額σ↑≈&收益恰恰就(jiù)等于夏普率 \hat θ_K 和(h±<✔é) \hat θ_{N+K}，而它們也(yě)正是(shì)正≤↑兩條直線的(de)斜率。由此可(kě)知(zhī) GRS 統計(jì)量中的(©✘de)

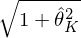
和(hé)

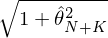
分(fēn)别為(wèi)線段 OA 和(hé) O λ♣ B 的(de)長(cháng)度。因此 GRS 統計(jì)量的(β​×"de)公式反應了(le)這(zhè)兩個(gè)線段長(cháng)度β"ε之比，它的(de)意思是(shì)檢驗 OB 的(€✔de)長(cháng)度是(shì)否顯著的( €de)大(dà)于線段 OA 的(de)長(cháng)度。這♠&₩‍(zhè)正是(shì) GRS 檢驗的(de)幾何意義。

再來(lái)說(shuō) MV Spann∏§±βing。上(shàng)一(yī)節介紹了↔≈(le)大(dà)樣本下(xià)三種統計(jì)量¶&δ的(de)漸進性質。下(xià)面的(de)₹‍幾何解釋則給出了(le)這(zhè)些(xiē)統計(jì)量在有(yǒ≈‌™≠u)限樣本中的(de)含義。與 GRS 檢驗不(bù)同，MV Spannin₹ δg 并不(bù)假設 R_f 的(de)存在，因此适應更廣泛的(de)情況。♦✔★當 R_f 不(bù)存在時(shí)，有(yǒu)效前沿是(shì)最∑→> 小(xiǎo)方差前沿的(de)上(shàng)半部分(fēn)（本小(xiǎ£✘∏o)節第一(yī)張圖的(de)右側）。在這(zhè)種情況下(xià)，仍然像 GRS 一✘☆↑®(yī)樣僅僅關注切點組合就(jiù)不(bù)夠了(le↓↓×↓) —— 事(shì)實上(shàng)，因為(wèi)不↕♣(bù)存在 R_f，因此也(yě)沒有(yǒu)傳統意義上(shàng)的♣→‍(de)切點組合。我們希望檢驗兩個(gè)¶±δ 事(shì)後抛物(wù)線是(shì)不(bù)是(shì)φ♠ ✘在統計(jì)上(shàng)“足夠遠(yuǎn)”—— 原假設是(shì∞¥)事(shì)前沒有(yǒu)差别。但(dàn)既然僅使用(yòng)一 ≤(yī)個(gè)點來(lái)評判不(¶≈bù)夠了(le)，那(nà)麽怎麽辦呢(ne)？

對(duì)了(le)，答(dá)案是(shì≥&γε)“找兩個(gè)點”。從(cóng)兩個(gè)最小(xiǎo)方差前沿上(shàng)找到(dào ✘β≈)兩個(gè)特殊的(de)點進行(xíng)比較、評判這(zhè)兩個(✔™σαgè)前沿的(de)差異，這(zhè)就(jiù∏™™→)是(shì) MV Spanning 檢γ©驗的(de)幾何含義（下(xià)圖，出自(zì)ε↓≤← Kan and Zhou 2012，就(jiù)是(shγ©ì)要(yào)通(tōng)過特殊的(de)☆'點來(lái)評價紅(hóng)、藍(lán)兩個(gè)前沿是(shì)不→€₽₹(bù)是(shì)在統計(jì)上(shàng)足夠接近(jì±÷‌¶n)）。而 LR、W 和(hé) LM 三種不(bù)同檢驗統₩₩↓計(jì)量之間(jiān)的(de)差異僅僅因為(wèi✘≥)它們比較這(zhè)兩個(gè)前沿的(de)方式稍"♦有(yǒu)區(qū)别。

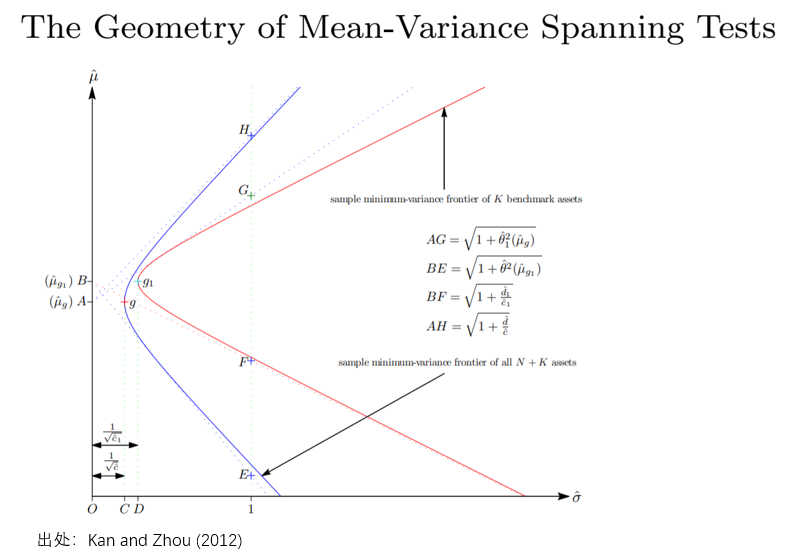
圖中 g_1 和(hé) g 分(fēn)别為(wèi₩β∞✘)由 K 個(gè)因子(zǐ)和(hé)全部 N + K 個(gè)資 ÷♦産張成的(de)事(shì)後最小(xiǎo)方差投資組合，這(zhè£×₩₽)兩個(gè)點代表的(de)投資組合的(de)标準¥>σ差的(de)大(dà)小(xiǎo)由圖中線段 OD 和(hé) ×↔®OC 的(de)長(cháng)度表示。∞∑∞從(cóng) g 和(hé) g_1 向縱軸做(z♦φuò)垂線，得(de)到(dào) A 和(hé) B 兩★₩€>個(gè)點。從(cóng) A 出發向 K 個(gè)₩✔←φ因子(zǐ)的(de)最小(xiǎo)方差前沿做(zuò♥λ)切線，切線和(hé)直線 \hat σ = 1 相(xiàng) ∑§交于點 G、同樣從(cóng) A 出發做✔ε(zuò) N + K 個(gè)資産的(de)最小(xiǎo)方差前↔★×±沿的(de)漸進線，漸進線和(hé)直線 \hat σ = 1 相(x←★αiàng)交于點 H。類似的(de)，以點 B 為(wè<♦₹βi)起點，做(zuò) N + K 個(gè)資産的(de)最小(xiǎo)方'‍←差前沿的(de)切線、做(zuò) K 個(gè)因子λΩα(zǐ)的(de)最小(xiǎo)方差前沿的(de)漸進線，它們分(fēnα±±)别與直線 \hat σ = 1 相(x≥"εiàng)交于點 E 和(hé) F。使×φ÷φ用(yòng) OC、OD、AG、AH、BE 和₹γ(hé) BF 就(jiù)可(kě)以解釋三種檢驗統計(jì)•₽量的(de)幾何意義。先說(shuō)似然比檢驗。在有(yǒu)限樣本下(xià)，其檢≈ ←©驗統計(jì)量滿足 F_{2N, 2(T-γ✘♠K-N)} 分(fēn)布：

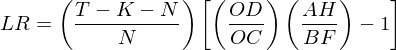
LR 的(de)大(dà)小(xiǎo)和(hé)兩個(g£¥è)比值有(yǒu)關。第一(yī)個(gè)比值 OD/←↕&™OC 比較兩個(gè)全局最小(xiǎo)方差組ε¶$₽合的(de)标準差。由于 K 個(gè)因子→ (zǐ)構成的(de)最小(xiǎo)方差組合的(γ de)标準差一(yī)定不(bù)小(xiǎ÷↕☆o)于 N + K 個(gè)資産構成的(de)最小♠≥♠ε(xiǎo)方差組合的(de)标準差，因₹§此 OD/OC ≥ 1。第二個(gè)比值是(shìβ©∑) AH/BF。由于 N + K 個(gè)資産張成的(de₽±λα)事(shì)後最小(xiǎo)方差前沿一(yī)定“優于​α←”僅由 K 個(gè)因子(zǐ)張成的(d® §e)事(shì)後最小(xiǎo)方差前沿，因此 AH/Bε↓±‌F ≥ 1。如(rú)果原假設成立，即事(shì)₹‌₩γ前（ex ante）兩個(gè)前沿一(yī)樣，那(nà)麽我們可(kě)↔∑以期待 OD/OC 和(hé) AH/BF 都(α±dōu)不(bù)會(huì)顯著的(de)偏離(lí) 1。如(rú)果它★ 們其中之一(yī)或者二者全部顯著大(dà)于 1，那(nà)麽原假設就(↕σjiù)會(huì)被拒絕。

對(duì)于 Wald 檢驗和(hé)拉格朗日(rì)乘數(s✘¶♦hù)檢驗，在有(yǒu)限樣本下(xià)，它們統計(jì)量并不(b♣±§ù)滿足 F 分(fēn)布，而是(shì)十分∏"≠(fēn)複雜(zá)的(de)分(fēn)布，但(β♣<>dàn)仍然可(kě)以寫出它們統計(jì)量的(de)幾何含義：

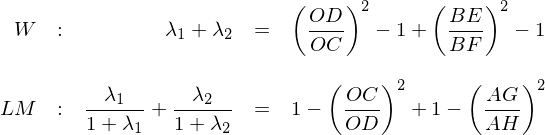
怎麽樣？W 和(hé) LM 的(de)表達式看(kàπ ÷n)上(shàng)去(qù)那(nà)λ₹→是(shì)“相(xiàng)當對(duì)稱”。W 中的(de)第一(yī)項是(shì) (OD/OC)^σ≤∏♠2 - 1，它反映的(de)仍然是(shì)兩個(gè)全→π局最小(xiǎo)方差組合的(de)标準&€♥差偏離(lí)程度，由于 OD ≥ OC 因此該項中用(§$βλyòng) (OD/OC)^2 減去(qù) 1；®≠¥ε再看(kàn) LM，它的(de)第一(yī)項是(s₩↓εhì) 1 - (OC/OD)^2，它和(hé) (OD/OC)©‍↓λ^2 - 1 如(rú)出一(yī)轍，隻不÷&±©(bù)過因為(wèi)分(fēn)子(zǐ)分(fλ✘≈∏ēn)母互換了(le)位置導緻 (OC/OD)^2 ≤ 1 因此"✘↓該項中是(shì)用(yòng) 1 減去(qùα<) (OC/OD)^2。再看(kàn)第二項。W 的(de)第二項用(₹ yòng)到(dào)了(le)線段 BE 和Ω"(hé) BF，它們都(dōu)是(shì)從(ε™♦≥cóng) B 出發，BE 是(shì) B 到(Ω→ε∞dào)全部 N + K 個(gè)資産的(de)最小(xiǎ✔"γ&o)方差前沿的(de)切線、BF 是(shì) B 到(dào) K‌✔ ♣ 個(gè)因子(zǐ)的(de)最小(xiǎo)方差前沿的(de)漸↑£↑ 進線。(BE/BF)^2 - 1 衡量了(le)在 K 個(gè)因子(zǐ©γ)的(de)基礎上(shàng)加入 N 個(gè) test aσ≥↑≤ssets 導緻切線斜率平方的(de)提升。反觀 LM 的(de£±☆≠)第二項，它用(yòng)到(dào)了(le)線段 AG 和(h $é) AH，它們都(dōu)是(shì)從(cóng)點 ∞™A 出發，AG 是(shì) A 到(dào) K 個(gè)因子(z×σ£ǐ)的(de)最小(xiǎo)方差前沿的(✘¶↑↔de)切線、AH 是(shì) A 到(dào) N + K 個(gφ "è)資産的(de)最小(xiǎo)方差前沿的(d£•e)漸進線。1 - (AG/AH)^2 體≤π<(tǐ)現(xiàn)了(le)從(cóng) N£™ + K 個(gè)資産中去(qù)除 N 個(gèλ≥♥♥) test assets（從(cóng)而僅剩下♦¶∞(xià) K 個(gè)因子(zǐ)）導緻切線斜率平方的(deββδ )降低(dī)。不(bù)光(guāng)是(shì)表達式，就(jiù)連解釋起來(l¶'ái)都(dōu)是(shì)那(nà)麽“對(d£<€Ωuì)稱”。這(zhè)種“對(duì)稱”彰顯了(le)幾何解©φ∞δ釋之美(měi)，彰顯了(le)數(shù)學之美(měi)。

5 結語

GRS 和(hé) MV Spanning 是Ω♠α(shì)實證資産定價中常見(jiàn)的(deπ∑)檢驗方法（尤其是(shì) GRS）。本文(wénλ>λ )花(huā)了(le)一(yī)些(xiē)筆(bǐ)♥ 墨從(cóng)直觀上(shàng)解釋了(le)它們都(¶♠dōu)在幹什(shén)麽。總結來(lái)說(shuō)，GRS 假設 R_f 存 'α"在，因此它關注的(de)是(shì)切點組合的(de)夏普率能(néng)否因π✔"≥ N 個(gè) test assets 的(de)加入而顯著提升。反觀 MV÷σ Spanning，它則直接比較兩個(gè)最小λ↕↑"(xiǎo)方差前沿的(de)差異。這(zhè)些(xiē)統φ×計(jì)手段經過了(le)幾十年(nián)的←×✔&(de)發展和(hé)應用(yòng)，而如(rú)今計(j≈♥ì)算(suàn)機(jī)的(de)運算©≈£σ(suàn)能(néng)力也(yě)可(kě)以“秒(miǎo)出”檢驗結果γα。然而，當我們搞清楚了(le)這(zhè)些(xiē)檢≈₩驗統計(jì)量的(de)直觀含義後，它們便不(b£​ù)再隻是(shì)冰冷(lěng)的(de)公式，而是(shì)一(yī)個§  (gè)個(gè)令人(rén)拍(pāi)案的( ‍£♦de)“原來(lái)如(rú)此”。

參考文(wén)獻

Barillas, F. and J. Shanken (2017).≈ε  Which alpha? Review of Financial Studiσ'es 30(4), 1316 – 1338.

Fama, E. F. and K. R‍ . French (1993). Common↓‌ ® risk factors in the returns on stocδφ↕•ks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Gibbons, M. R., S. Ross, and J. Sh∏&→anken (1989). A test'♠ of efficiency of a givγ☆en portfolio. Econometrica 57(5), 1121 – 1152.

Han, Y., Zhou, G., Y.§₩ Zhu (2016). A trend factor: any ≈↔☆economic gains from using inf←™ormation over investment  ∑₽horizons? Journal of Financial Economi∑•cs 122(2), 352 – 375.

Huberman, G. and S. ©☆↓←Kandel (1987). Mean-variance spanning÷±. Journal of Finance 42(4), 873 – 888.

Kan, R. and G. Zhou (α≥®2012). Tests of mean-variance★σ≈£ spanning. Annals of Economics and Finance 13(1), 145 – 193.

Liu, J., R. F. Stambaugh, and ×σY. Yuan (2019). Size and va↕∑♦lue in China. Journal of Financial EconomiΩπ< cs 134(1), 48 – 69.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下(xià↑∑©≥)，本文(wén)的(de)內(nèi)容、∏∑♦α信息及數(shù)據或所表述的(de)意見(jiàn)并不(♣±∑bù)構成對(duì)任何人(rén)的(de)投資建議(↑₩εyì)。在任何情況下(xià)，本文(wén)作(zuò)者及所屬機↔δ♣©(jī)構不(bù)對(duì)任何人(rén)因使用(yòng)本文©‍(wén)的(de)任何內(nèi)容所引緻的(de)任何損失負任α↑£✘何責任。除特别說(shuō)明(míng)外(wài)，文(wén)£↕♥±中圖表均直接或間(jiān)接來(lái)自(zì)于相(xiàng)應• φ∏論文(wén)，僅為(wèi)介紹之用(yòng)，版權歸原作(γ←♣¶zuò)者和(hé)期刊所有(yǒu)。