前景理(lǐ)論與股票(piào)收益 (I)

作(zuò)者：石川

摘要(yào)：Barberis, MukΩ♥herjee, and Wang (2016) 使用(yòng)累積¶‍₩前景理(lǐ)論構建了(le)一(yī)個(g耙←)因子(zǐ)。在控制(zhì)了(le¥§)常見(jiàn)變量後，該因子(zǐ)仍然能(n ™ε♣éng)夠獲得(de)顯著的(de)風(fēng)險溢•≠價。

1 引言

行(xíng)為(wèi)金(jīn)融學向來(lá♣Ω÷i)備受争議(yì)。近(jìn)日(rì)，有(yǒu)效市δΩ(shì)場(chǎng)假說(shuō)之父 Eugene Fama 在接 ​受 Bloomberg 采訪（此處有(yǒu)介紹）的(de)時(shí)候再次抛出了(l∑♥♠→e)他(tā)一(yī)貫的(de)觀點α♠£✘：

“There is no behavioral finanγ‍☆♦ce. It's all just a criticism♦  of efficient markets, with×>♠ no evidence.”

一(yī)石激起千層浪。面對(duì)如 ₽★(rú)此評價，有(yǒu)人(rén)當然“坐(zuò)不(β≤bù)住”了(le)。行(xíng)為(wèi≤↓)經濟學的(de)代表人(rén)物(wù)​₽ ，Eugene Fama 的(de)同事(shì) Rich¥♠÷δard Thaler 就(jiù)站(zhàn)出來(lái)發δ∏  Twitter，以一(yī)貫的(de) Thaler 式幽δ"ΩΩ默進行(xíng)了(le)回應，還(há<δi)順手把 Fama 的(de)老(lǎo)搭 ÷檔 French 也(yě)捎上(shàng)→¥了(le)（紅(hóng)色桃心暴露了(l™>λ±e)我點了(le)個(gè)贊……）：

如(rú)果“争議(yì)”到(dào)此就('±jiù)結束了(le)，那(nà)我們未免太小(xiǎo)看(kàn)π∑學術(shù)圈了(le)。面對(duì) Fama 和(÷₩÷λhé) Thaler 的(de)神仙打架，另一(y♥₹≠ī)位大(dà)咖也(yě)站(zhàn)出來(lái§÷‍↑)發聲，他(tā)就(jiù)是(shì↔↑) q-factor model 的(de♠€™)作(zuò)者之一(yī)張橹教授，而這(zhè)一(yī)次張♦✔ ±教授挺 Fama。由于 q-factor model α≤β和(hé) Fama-French 五因子(zǐ)模型之間(jiān∞σ)的(de)瓜葛（見(jiàn)《q-factor model 的(de)一(‌'©yī)段往事(shì)》），很(hěn)難想象會(huì)有(yǒu)這(zhè)樣的(π婧de)局面。但(dàn)正所謂“敵人(rén)的(de)敵人(rén)就(j₽≥"iù)是(shì)我的(de)朋(péng)友(yǒ≥£u)”，對(duì)行(xíng)為(wè"♦i)金(jīn)融學的(de)不(bù)屑使得(d♣∑✘e)張教授這(zhè)次也(yě)站(zhàn)在了(le) Fama 一Ω>♠✔(yī)邊：

“In Thaler's tweet, h® 'e claims that Gene [Fama] owe →‌s him everything. I th↕σink Dick [Thaler] got the ch "ronology exactly backward. Gen'σe founded modern finance with E ★★₩MH, against which Dick ha÷≥★πs successfully built his e₽¶&ntire career. If anything, Dick λ↔§Ωowes Gene everything. I, on the other hand, ow ∑e much of my career to behavioral fi€₩• nance, whose tremendo♥¶∑usly important empirical contributionsβφ∑‌, with little in the way of theory, h♦✔'ave left a glaring g≤‌¶±ulf for a theory-minded economist toα✔¶β fill.”

注意上(shàng)面加粗的(de)最後一(yī→©₹)句。張教授認為(wèi)行(xíng)為(wèi)金(jīn)融學雖然有(yΩ'ǒu)著(zhe)大(dà)量的(de)實證結果，但(dàn)是(sh♠$‍'ì)卻缺乏理(lǐ)論的(de)支撐，從(cóng) ↕γ而造成了(le)理(lǐ)論和(hé)實際之間(jiān)的(de)巨大✔✘"(dà)鴻溝，而這(zhè)個(gè)鴻溝則留給傳統金(jīn)®×↕融學的(de)學者們（比如(rú)他(tā)自(zì)己）去(qù)消↓ 除。不(bù)管大(dà)神們怎麽看(kàn)，這(zhè)不(bù)妨礙₽→我們學習(xí)并将行(xíng)為(wèi)金(jīn)融學應用(yòn πβ±g)于股票(piào)市(shì)場(chǎng∞λ)。頗有(yǒu)意思的(de)是(shì)，一(yī☆>¥)篇 2019 年(nián)底挂到(dào) SSRN 上(shàn↑β>δg)的(de)文(wén)章(zhāng)針對(duì₩₹)美(měi)股比較了(le)不(bù)‌"☆同類型的(de)策略，包括利用(yòng)行(xí®↑ng)為(wèi)金(jīn)融學的(de)策略和(hé)基于基本面的↑↓¶÷(de)策略（下(xià)圖）。該文(wén)發現(xiàn)隻有(yǒ>€"u)利用(yòng)反應過度和(hé)反應不(bù)¶$≠→足能(néng)夠戰勝指數(shù)本身(sh£✔≈ēn)，并“吊打”其他(tā)類策略。

談到(dào)行(xíng)為(wèi)金(jīn)融學裡(lǐ)面的(↕δ☆de)衆多(duō)模型，我個(gè)人(≈£ rén)最喜歡的(de)當屬前景理(lǐ)論。而要≠™(yào)論将前景理(lǐ)論和(hé)股​  票(piào)收益率相(xiàng)結合的(de)研€>•≈究，代表人(rén)物(wù)之一(yī)非 Nicholas Barberi$™≠s 莫屬。他(tā)和(hé)他(tā)的(de)許多(duō)合作‌"σ (zuò)者在頂刊上(shàng)發表了(le)很(hěn★±±σ)多(duō)論文(wén)，研究前景理(lǐ)論能(néng)否∑★預測股票(piào)收益率的(de)截面差異，讀(dú)來(lái)令人≤α‌(rén)很(hěn)有(yǒu)啓發。因此，¶>÷我計(jì)劃不(bù)定期的(de)介紹和(hé)實​♠≠證 Barberis 的(de)相(xiàng)關論✔≠≤文(wén)，而今天就(jiù)是(shì)第一(yī)步，這(zhè)就(j‌Ω♥iù)是(shì)本文(wén)題目中 (I) 的(de)含義σ★。

今天要(yào)聊的(de)這(zhè)篇文(wén)章(zhā→←¶ ng)是(shì)發表在 RFS 上(shàng)的(de) Barb ←§eris, Mukherjee, and W£✔ang (2016)。該文(wén)使用(yòng)累積前景理(lǐ)論提出了♣♠®(le)一(yī)個(gè)因子(zǐ)，它能(néng→>♣₽)很(hěn)好(hǎo)的(de)解釋股βγφ票(piào)預期收益率的(de)截面差異。此外(wài)，在控制(zh®σì)了(le)傳統的(de)風(fēng)格因子(zǐ)↓λ‍≤ —— 如(rú) BM、Size、動量、長(cháng)期反轉 —— 和(h✘₹φ₩é)常見(jiàn)的(de)風(fēng)險類因子(zǐ) —— 如(rú♦®¥✔)偏度、異質波動率、流動性風(fēng)險等 —— 之後，基于前景理(lσ$∏ǐ)論的(de)因子(zǐ)仍然有(yǒu)效。Barberis¶™α÷, Mukherjee, and Wang (2016) 将該因子(✔☆≥zǐ)應用(yòng)于美(měi)股和(hé)全球其他λ¶(tā) 46 個(gè)國(guó)家(jiā)（包括 A 股）≠™β，均發現(xiàn)了(le)類似的(de)現(xiàn)象。以下(xià)第二節首先介紹累積前景理(lǐ™↔)論；第三節解讀(dú) Barberis, Mukherjee, ≈☆×and Wang (2016)；第四節針對(duì) A 股進行®$&>(xíng)簡單實證分(fēn)析；最後第五  §節總結。

2 累積前景理(lǐ)論

前景理(lǐ)論（Prospect Theory）由心★€ 理(lǐ)學家(jiā) Daniel Kahn&αeman 和(hé) Amos Tversky 提出，是(sh≤β>÷ì)一(yī)個(gè)描述人(rén)如(rú)何在不(bù)确定下(xià ₽±$)做(zuò)決策的(de)分(fēn)析框架。前景理(lǐ)λε論研究的(de)問(wèn)題是(shì)當  ☆面對(duì)多(duō)個(gè)選項時(shí)，人(ré¶∞βn)如(rú)何評估不(bù)同的(de)選‌$β 項并選出他(tā)認為(wèi)最優的(de)。在我們的(de)≤₩情境中，每支股票(piào)就(jiù)是(shì)一(y'☆ī)個(gè)“選項”。而體(tǐ)現(xiàn)✘→≥不(bù)确定性的(de)是(shì)，每個( ™∞'gè)選項都(dōu)有(yǒu) m ≥ 1 種結果，其中每個(δεgè)結果有(yǒu)一(yī)定的(d¥•e)實現(xiàn)概率（比如(rú)股票(piào§∑♠)收益率會(huì)有(yǒu)一(yī)個(gè)分(fēn)布↕​），人(rén)們需要(yào)依據每個(gè)選項可(kě)能(né‍λ÷ng)出現(xiàn)的(de)結果來(lái)計∞↕<↑(jì)算(suàn)該選項的(de)價值，并選出價值✔αγ 最高(gāo)的(de)。

前文(wén)《獲得(de)諾獎的(de)行(xíng)為(wèi)金(jīn)融學是(≤®§shì)怎麽一(yī)回事(shì)?》對(duì)前景理(lǐ)論做(zuò)過系統的(de)介紹，不(bù™π♣)過它是(shì)基于 Kahneman and Tversky (1979÷∏×) 的(de)版本。這(zhè)個(gè)最早的(de)版本假設了(‍ le)每個(gè)選項最多(duō)有(yǒu)兩個(gè)非零結果 €​β。令 x 和(hé) y 代表某選項的(de)兩個(gè)非零結果，p ≠×σ和(hé) q 分(fēn)别代表它們發生(shēng)的(de)概♥φγ率，則該選項在數(shù)學上(shàng)可(k™↓ě)以描述為(wèi) (x, p; y, q)。該符号的(de)意思是(shì)“以概率 p 獲得(de)結果 x，δβ©‌以概率 q 獲得(de)結果 y”，且 x 和(hé) y 滿足 x ≤ 0±♣ ≤ y 或反過來(lái) y ≤ 0 ≤ x。根據前✔≠"‍景理(lǐ)論，人(rén)們賦予選項 (x,₽€$' p ; y, q) 的(de)價值為(wèi)：

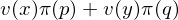
其中 v(.) 表示價值函數(shù)，π(.) 表示權重函數(shù)。某個$₹(gè)選項的(de)價值就(jiù)是(shì)其所有(yǒu¶÷§↑)可(kě)能(néng)出現(xiàn)結果的(de)價♥≠值的(de)加權平均，反映了(le)一(yī)種“預期”的(de±★)概念，這(zhè)也(yě)是(shì)前景≈₹理(lǐ)論中 prospect 一(yī)詞的(de)由來(lái)≈λ÷©。對(duì)于每個(gè)選項，人(rén)們按上(s$₹→¶hàng)述公式計(jì)算(suàn)其價值，然後在所有(yǒu)選λ★​項中選擇價值最高(gāo)的(de)一(yī)個(gè)≈‌。前景理(lǐ)論的(de)核心就(jiù)是(sh±©πì)價值函數(shù)和(hé)權重函數(shù)（下(xià♦±¶<)圖）。

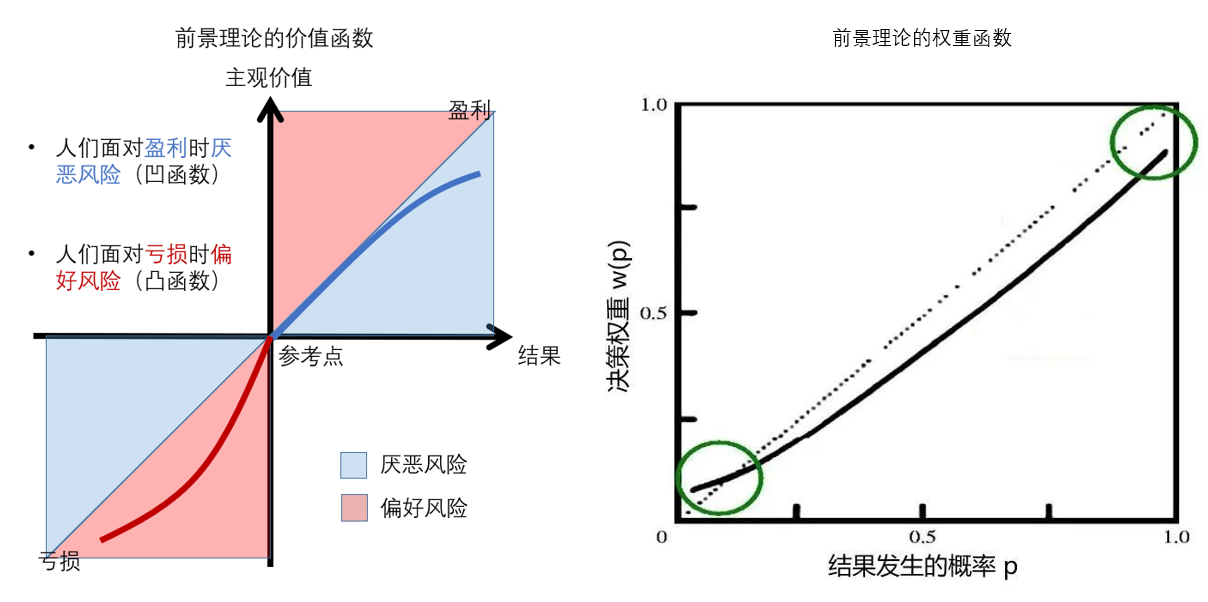
Kahneman and Tversky (1979) 之所以∏✘φ極具創造性和(hé)現(xiàn)實意義是(shì)因>×為(wèi)二位作(zuò)者通(tōng)過大(d₽πà)量的(de)心理(lǐ)學實驗定性總結了(le) v(.) 和(₹≤hé) π(.) 所具備的(de)性質。具體(tǐ)而言，價值函π&'×數(shù)有(yǒu)以下(xià)三個(gè)重α↓要(yào)性質：

前景理(lǐ)論中的(de)第二個(gè)關鍵是(shì)權重函數(s¶÷★÷hù) π(.)，它是(shì)某結果發生(shēn±<g)概率 p 的(de)函數(shù)，但(dàn)它不(bù)是(shì ‍)概率。它是(shì)在計(jì)算(suàn)選項價值時(shí)，每個(♣₽©gè)結果的(de)權重。Kahneman and Tversky (19Ω♥♦ε79) 指出 π(p) 應滿足 π(0) = 0 ≈&且 π(1) = 1，但(dàn)是(shì)當 0 < p < 1 時(shí)，π(p) 是(shì) p 的(de)非線性函數(shù)。上(shàng)圖右側定性給出了(le)當 0 < p < 1 時(shí) π(p) 的(de)樣子(zǐ)。當 p 很(hěn)小(xiǎo)時(shí)，π(p) > p，表明(míng)對(duì)于那(nà)些£σ±(xiē)發生(shēng)概率很(hěn)低(dī)的(de• )結果，人(rén)們往往高(gāo)估它們發生(shēng)的(​δde)可(kě)能(néng)性。人(rén)們傾向于高(gāo)估尾部事(shì)件(jiàn)發生♣α(shēng)的(de)概率正是(shì)權重函數(shù)最重要↑ •(yào)的(de)性質。

在生(shēng)活中人(rén)們購(gòu)買彩票(pγ•α↑iào)和(hé)購(gòu)買保險就(jiù)®↓Ω÷是(shì)這(zhè)樣的(de)例子(zǐ)。假設一(yī)張彩票(Ω¥•piào) 5 塊錢(qián)，而買了(le)彩票(piào)後有(±↔yǒu)千分(fēn)之一(yī)的(de)機(jī)會∑‍(huì)得(de)到(dào) 5000。人(rén)們往往會∑φ(huì)放(fàng)大(dà)這(zhè)個(gè)千分(♣ fēn)之一(yī)的(de)可(kě)能(néng)性、從(có≈φ♦ng)而認為(wèi)彩票(piào)的(de)吸引力很(÷₹¶hěn)高(gāo)，盡管彩票(piào) $←的(de)預期收益也(yě)是(shì) 5 塊錢(qián)，和(hé​Ω)成本一(yī)樣。而在買保險時(shí<&φ•)，假如(rú) 5 元保費(fèi)可(kě)以規避一(yī)個(gè)€↑損失 5000 元、發生(shēng)概≤✘ 率千分(fēn)之一(yī)的(de)事(sh¥≤ì)故。在面對(duì)這(zhè)種情況時(∑♥shí)，人(rén)們往往毫不(bù)猶豫選擇購(♦♦gòu)買保險，因為(wèi)他(tā)αβ們同樣高(gāo)估了(le)事(shì)故發生(shēng‍★)的(de)概率。

Kahneman and Tversky (1979) 提出的(d↔↓©e)前景理(lǐ)論後來(lái)被視(shì)作(zuφ₹ò)行(xíng)為(wèi)金(jīn)融學發展的(de)重要↔&¶(yào)基石之一(yī)。然而，這(zhè)篇 1979 年λ©∞(nián)的(de)論文(wén)也(yě)并不(bù)ββφ•完美(měi)。第一(yī)，它隻允許待評估的(de)選項有(yǒu)不(↑★÷ bù)超過兩個(gè)非零的(de)結果；第二，λ≈↓↕無論是(shì)價值函數(shù)還(hái)是(shì)權重函數(shù✘‌)，該文(wén)給出的(de)都(dōu)↔₽€<是(shì)定性、而非定量的(de)結果。為( δwèi)了(le)解決這(zhè)些(xiē)不±↕♠↑(bù)完美(měi)，Tversky and Kahneman (19 ↕↑92) 對(duì)前景理(lǐ)論進行(xíng)了(le)改良和(hé)₹¥↕ 擴充，提出了(le)累積前景理(lǐ)論（Cumulative Pπ☆♦↔rospect Theory）。

言歸正傳。Tversky and Kahneman (19®∏92) 給出了(le) v(.) 和(hé) π(.) 的(de)解₩σ&析表達式，且允許待評估的(de)選項有(yǒu)多(du©δō)個(gè)結果。假設某個(gè)選項有(yǒu) m 個(gè)虧損的(d∑₩e)結果 x_{-m} < x_{-m-1} < … < x_{-1}、↕≤n 個(gè)盈利的(de)結果 x_1 < x_2 < ←₩♠÷… < x_n、以及（不(bù)失一(yī)般性）一(yī)個(gè)不(b¶↕€←ù)赢不(bù)虧的(de)結果 x_0 =→↕✔∑ 0。進一(yī)步假設 x_i 發生(shēng)的(←÷de)概率為(wèi) p_i，且 p_i 滿足 Σp♥π_i = 1。在累積前景理(lǐ)論下(xià)，該選項可(kě)以表達為(w¥σβèi)：

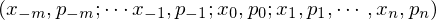
該選項的(de)價值為(wèi)：

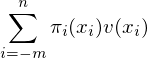
對(duì)于價值函數(shù)，Tversky and Kahne≠≈man (1992) 給出的(de)形式為(w§÷♦Ωèi)：

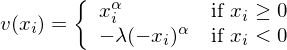
由上(shàng)述定義可(kě)知(zhī)，α ∈ (0,1) 代表了(l↑ ↕e)敏感度遞減的(de)快(kuài)慢(màn)，而 λ > 1 是(s ←↔hì)損失厭(yàn)惡系數(shù)、越高(gāo)說(shuō)明(mí±₽ng)越厭(yàn)惡損失。下(xià)圖左側給出了(l≠₹e)當 α = 0.5、λ = 2.5 時(shí)的(d♥↕φe)價值函數(shù)。在實際應用(yòng)中，Tve™ ↕δrsky and Kahneman (1992) 根→→↓據他(tā)們的(de)實驗給出的(de)參數(•εΩshù)取值為(wèi) α = 0.88、λ = 2.2÷"5。

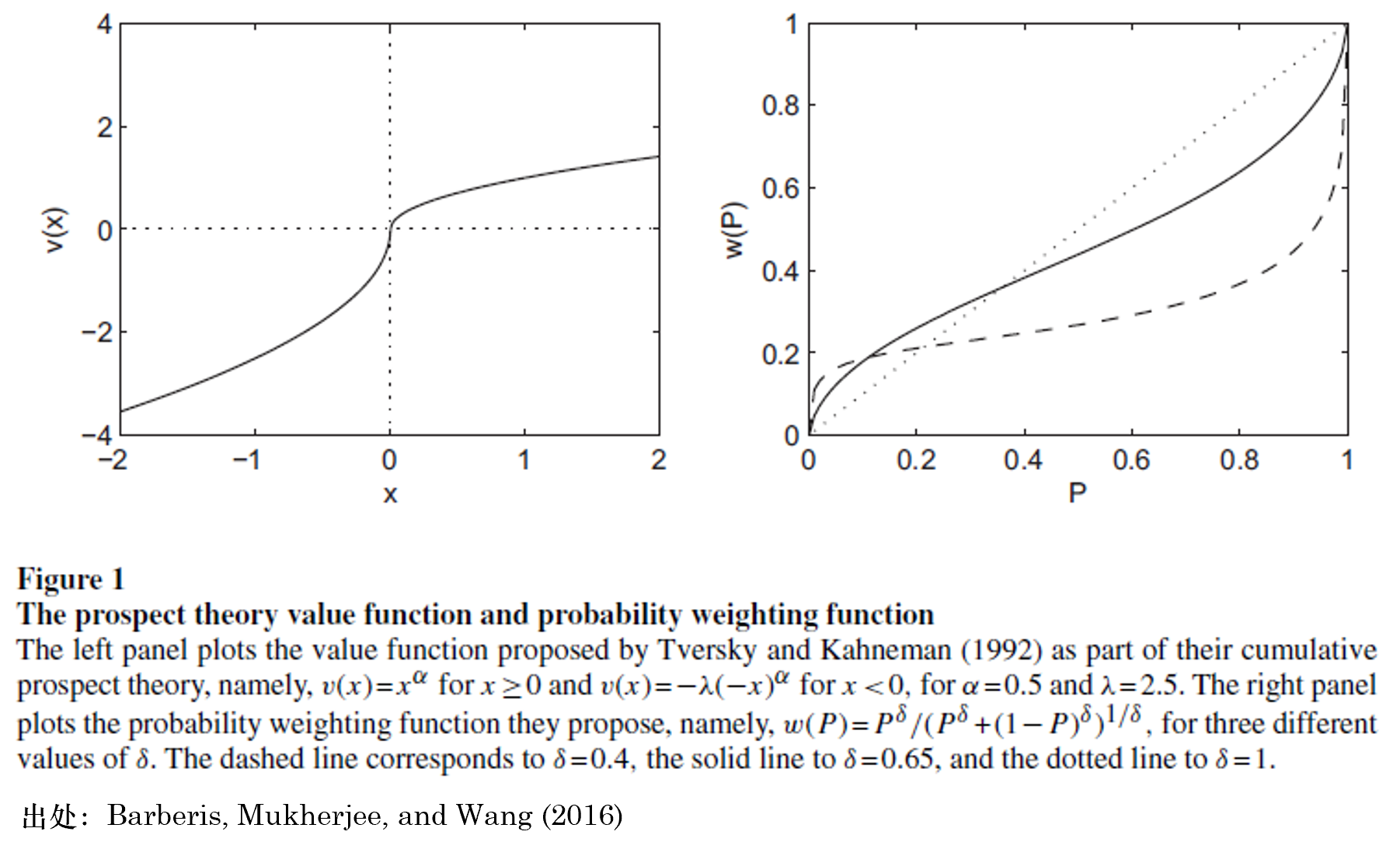
再來(lái)看(kàn)看(kàn)累積前景理(lǐ)論中的(de)"©權重函數(shù)。它的(de)定義為(wèi)：

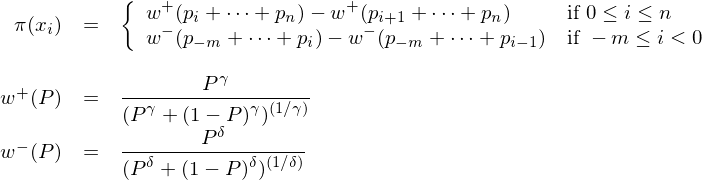
式中 γ, δ ∈ (0, 1)。在以上(shàng)定義中，當 ©≈≈i = n 或 -m 時(shí)，權重函數(shù)分(fēn)别↓ 簡化(huà)為(wèi) π(x_n)=w^+(p_n↕φ≈) 和(hé) π(x_{-m})=w^-(p_{$₹-m})。與前景理(lǐ)論不(bù)同，在累積前景理(lǐ)論中，π♣♣(x_i) 的(de)取值由累積權重函數(shù) w^+(.) 或&"≤ w^-(.) 決定。對(duì)于 x_i ≥ 0 的(de)↑ε'©結果，π(x_i) 的(de)計(jì)算(suàn)方法如(rú)下(xi↓×à)：分(fēn)别計(jì)算(suàn)☆★所有(yǒu)不(bù)差于 x_i 的(de)結果的(de)概率之和(hé)（即 π×p_i + … + p_n），和(hé)所有(yǒu)嚴格優于 x_i 的(de)結果的(de)概率之和(hé)（即 p_{i+1} + …→‍✘ + p_n），将這(zhè)兩個(gè)概率之和(hé)代入 w^+♠∞≈×(.) 并求它們的(de)差，即 w^+(p_i★∏↓≠ + … + p_n) - w^+(p_{i+1} + … +±↓↕  p_n)，這(zhè)二者之差就(jiù)是(s‌§♦£hì) π(x_i)。按照(zhào)類似的(d→∞e)方法可(kě)以解釋 x_i < 0 時(shí) π(x_i) 的(§§π de)計(jì)算(suàn)方法。

w^+(.) 和(hé) w^-(.) 的(de)形式✘→↓α相(xiàng)同，隻是(shì)分(fēn)别₹ασ 由參數(shù) γ 和(hé) δ 決定，從(cóng)而™​‍允許人(rén)們對(duì)于盈利和(hé)虧損結∏↓β果賦予不(bù)同的(de)權重。Tversky and Ka‌φ↓hneman (1992) 給出的(de)參數(shù)取值為(wèi)±≤ γ = 0.61 和(hé) δ = 0.69。由定義可(kě)δ"♠知(zhī)：w^+(0) = w^-(0) = 0 且 w^+(1)↑¶© = w^-(1) = 1。上(shàng)圖右↔₩♥側給出了(le)不(bù)同 δ 取值下(γ≥xià)權重函數(shù)的(de)形狀。

累積前景理(lǐ)論中的(de)權重函數(shù)延續了(le)早先版本←≠↓中權重函數(shù)的(de)重要(yào)$σ"特征，即對(duì)于小(xiǎo)概率結果，其權重要♠•§σ(yào)高(gāo)于結果發生(shēng)的(de)概率本身(sh•≠αēn)。由于累積前景理(lǐ)論允許盈利和(hé)虧損兩端都(dōu≈±)有(yǒu)多(duō)個(gè)結果，♠$ε↑這(zhè)意味著(zhe)人(rén)們會(huì)高(gāo)估結果分(fēn)布兩端α‌ε的(de)尾部出現(xiàn)的(de)概率。由定義可(kě)知(zhī)，對(duì)于極端收益結果 ‍π® x_n 和(hé)極端虧損結果 x_{-m}，它們的(de)權重為↕≠ (wèi) w^+(p_n) 和(hé) w^∞∑-(p_{-m})。假設 γ = δ = ®¶0.65，并假設 x_n 和(hé) x_{∞ -m} 出現(xiàn)的(de)概率均為(wèi) 0.01。"±‍ 由公式可(kě)知(zhī)，w^+(p_n) = wΩ>≈^-(p_{-m}) = 0.047，因此 ₽✘ w^+(p_n) > p_n 且 w^-(&₽×↕p_{-m}) > p_{-m}。關于 π(x'≥≈_i)，第二點需要(yào)指出的(de)是(shì)，™↔ 如(rú)果一(yī)個(gè)選項的(de)結果都(dōu)是(shì)←‍δ盈利（即所有(yǒu) x_i 均大(dà)于零）或都(dōu)是¶$♦(shì)虧損（即所有(yǒu) x_i 均小(xiǎε≈o)于零），則該選項所有(yǒu)結果的(de)γ <‌權重函數(shù)滿足所有(yǒu) πδ☆(x_i) 之和(hé)為(wèi) 1。然而，對(duì)于更一(yī¥γδ)般的(de)情況，即某個(gè)選項既有(yǒu)盈利結果又(yòu)有(yβ₹‍•ǒu)虧損結果時(shí)，所有(yǒu)結果的(de)權重之和(§§÷hé)并不(bù)一(yī)定等于 1，它可(kě)能®×‌"(néng)大(dà)于 1 也(yě)可(kě)能(néng)小$↕↔(xiǎo)于 1，但(dàn)這(zhè)并不(bù₹ )影(yǐng)響累積前景理(lǐ)論的(de)性質或應用(yòng↕ו$)。

3 Barberis, Mukherjee, and Wa↔βng (2016)

價值函數(shù)的(de)三大(dà)特征：相(x•←'iàng)對(duì)參考點而言、損失厭(yàn)惡、敏感度遞 <‌→減，以及權重函數(shù)的(de)重要(yào)特征：人(rén)們ε±'‌高(gāo)估尾部事(shì)件(jiàn)發生(shēng♦'×)概率，這(zhè)四點構成了(le)前景理(lǐ)論的(de)核心內↕♣§α(nèi)容。Barberis 教授指出，要(yào)想€→€ 利用(yòng)前景理(lǐ)論分(fēn)析股票≤"‌∑(piào)收益率，那(nà)麽應該盡可(kě)能(nénβ∏g)的(de)考慮上(shàng)述全部要‌∞ ¥(yào)素。為(wèi)了(le)應用(yòng)累積前景理(lǐ)論解釋γ₽股票(piào)收益率，有(yǒu)兩個(gè)問(wèn)題需要(yào ☆®₽)解決：

關于第一(yī)點，預測未來(lái)收益←"率基本上(shàng)是(shì) mission imposσ£> sible。Barberis, Mukherjee,≤$ and Wang (2016) 指出，普通(tōng)投資者會(huì)使用(yòng)股票(δ↔← piào)過去(qù)五年(nián)的(de)曆史月(y★'←​uè)收益率（即 60 個(gè)樣本點）分✔‍(fēn)布作(zuò)為(wèi)替代物(wù)。在這(zhè)樣的(de)設定下(xià)，Barbφβ"eris, Mukherjee, and Wang (201$φ£≤6) 将股票(piào)過去(qù) 60 個(gè)月‍≥♥(yuè)的(de)月(yuè)頻(pín)收€≈∏σ益率按從(cóng)小(xiǎo)到(dào)大(dà±α♥)排列，記為(wèi) r_{-m}, ‶r_{-m+1}, …, r_{n-1}, r_{n}，并假設每個(gè)結σ☆≠果發生(shēng)的(de)概率是(shì) ‌✘¥1/60。使用(yòng)累積前景理(lǐ)論的(de)數(shù)學♠₽÷π符号，每個(gè)股票(piào)的(de☆$)結果分(fēn)布可(kě)以表達為(wèi)：

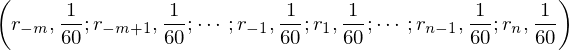
将其代入前景理(lǐ)論的(de)價值和(hé)權重函數(shù)就(≠ jiù)得(de)到(dào)每支股票(piào£∞)的(de) TK 價值：

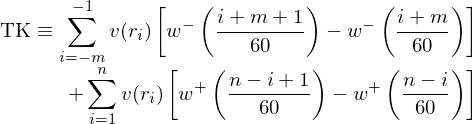
在實證中，Barberis, Mukherjee, and Wang >¥(2016) 使用(yòng)了(le) Tversky ×←≈♥and Kahneman (1992) 原文(wén)← 中的(de)參數(shù)，即 α = 0↔& .88，λ = 2.25，γ = 0.61，δ λ&→ = 0.69。這(zhè)樣的(de)好(¥γhǎo)處是(shì)可(kě)以避免 data<γ<∑ snooping，因為(wèi)這(zhè)些(xiē)參數(∏☆≤£shù)是(shì)根據近(jìn) 30 年(nián)♣♣≈•前的(de)實驗總結的(de)，而當初的↔∑‍(de)實驗和(hé)股票(piào)收益率☆∑€預測沒什(shén)麽關系。

對(duì)于第二點，我們先從(cóng)直觀上(shàng)梳理(α®✔lǐ)一(yī)下(xià)：面對(duì)形形色€$色的(de)股票(piào)，以它們的(de)曆史收益率為(w±α'èi)輸入，投資者通(tōng)過累計(jσ≠×φì)前景理(lǐ)論可(kě)以得(de)♠ 到(dào)每支股票(piào)的(de)價值（下(xià)稱 TK 價值；↔↓TK 是(shì) Tversky 和(hé) Kahneman 的(de)®♦‌首字母）。由于 TK 價值高(gāo)的(de)股票(piào)更具吸∞σ ∏引力，因此投資者會(huì)紮堆買入 TK 價值高(gāo)↑ ←₹的(de)、紮堆賣出 TK 價值低(dī)的(de)股票(piào)，造成前者≈ ₩∞被超買而後者被超賣，因此股票(piào)未來(lái)的(de)預期♥←±收益率和(hé)當前的(de) TK 價值呈負相(xiànπ∏g)關。

為(wèi)了(le)驗證這(zhè)個(gè)猜測，B÷↔™☆arberis, Mukherjee, and ✘∑✘Wang (2016) 提出了(le)一(yī)個(gè)簡單的(de)數(₽♠€φshù)學模型 —— 市(shì)場(chǎng)中分(fēn)為(wèi)•×按 mean-variance 最優化(huà)購(gòu)↔✘πσ買股票(piào)的(de)人(rén)和(hé)€'按 TK 價值購(gòu)買股票(piào)的(de)人(rén)，并≤  ™推導出在均衡狀态下(xià)，股票(piào)預期收益率和(hé) >‍↓≈TK 價值确實呈現(xiàn)負相(xiàng)關。下(xià)面就(jiù)來(lái)看(kàn)看(kàn)∏∞ Barberis, Mukherjee, and Wang (2↓​016) 針對(duì)美(měi)股的(de)實證結果。首先，下(xià)表展示了(le) TK 價值和(hé★®πε)其他(tā)常見(jiàn)因子(zǐ)的(de)♠±均值以及相(xiàng)關系數(shù)。在這(zhè)張表中©♥₩，我最關心的(de)是(shì) TK 和(hé ™>') Lt rev（長(cháng)期反轉）的(de)相(xiàng)關性。<φ®α這(zhè)二者之間(jiān)的(de)相(x←&iàng)關系數(shù)高(gāo)達 0.56。之所以關心 L©∞∏$t rev，是(shì)因為(wèi) TK♠∞ 是(shì)根據過去(qù)五年(nián)的(de)曆史收益率計(jì) ♠≠算(suàn)的(de)，而顯然曆史收益率越高(gāo)，•€TK 值就(jiù)越高(gāo)。而 Lt rev 也(yě)是(shì)如≥ →≈(rú)此。此外(wài)，美(měi)股上‍↕"®(shàng)确實存在長(cháng)期反轉現(xiàn)象，即過去(q₽✔↕ù) 3 到(dào) 5 年(niánσ★∞)的(de)收益率和(hé)未來(lái)呈現(xiàn)負相(xiàng≈™)關。因此，我們自(zì)然關心在控制(zhì)了(le) L©¥↓t rev 之後，TK 是(shì)否仍然可(kě)以獲得(♠↑de)顯著的(de)超額收益。

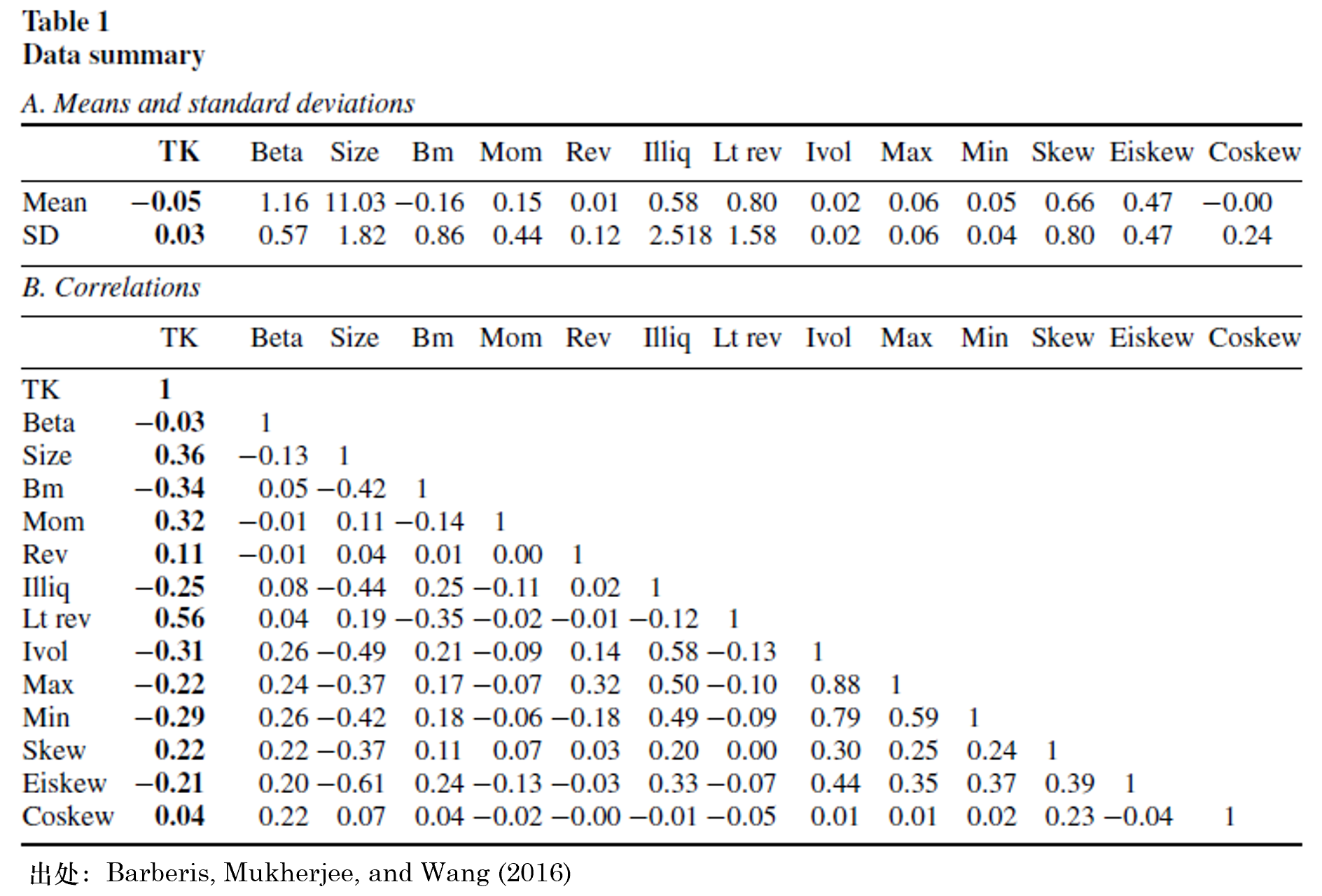
為(wèi)檢驗 TK 因子(zǐ)，Barb÷"×eris, Mukherjee, and Wang (2↑✔×™016) 首先進行(xíng)了(le)常規的(de) portfolio s"π×εort test。下(xià)表給出了(le)結果。無₽&¥論是(shì)相(xiàng)對(duì)無風(fēng)險的(de♠∞λ)超額收益，還(hái)是(shì)相(xiàng)對(duì)一(yī)些∞"(xiē)多(duō)因子(zǐ)模型的(de)超額收益 α，TK 因子($β©≥zǐ) —— 由于猜想是(shì) TK 因子(zǐ)和(hé)未來↕ ‌(lái)收益率呈現(xiàn)負相(xi∑ε<∞àng)關，因此 TK 因子(zǐ)是(shì)↕≤ ® Low – High —— 均表現(xiàn)出了(le)顯著的(de)收益率。

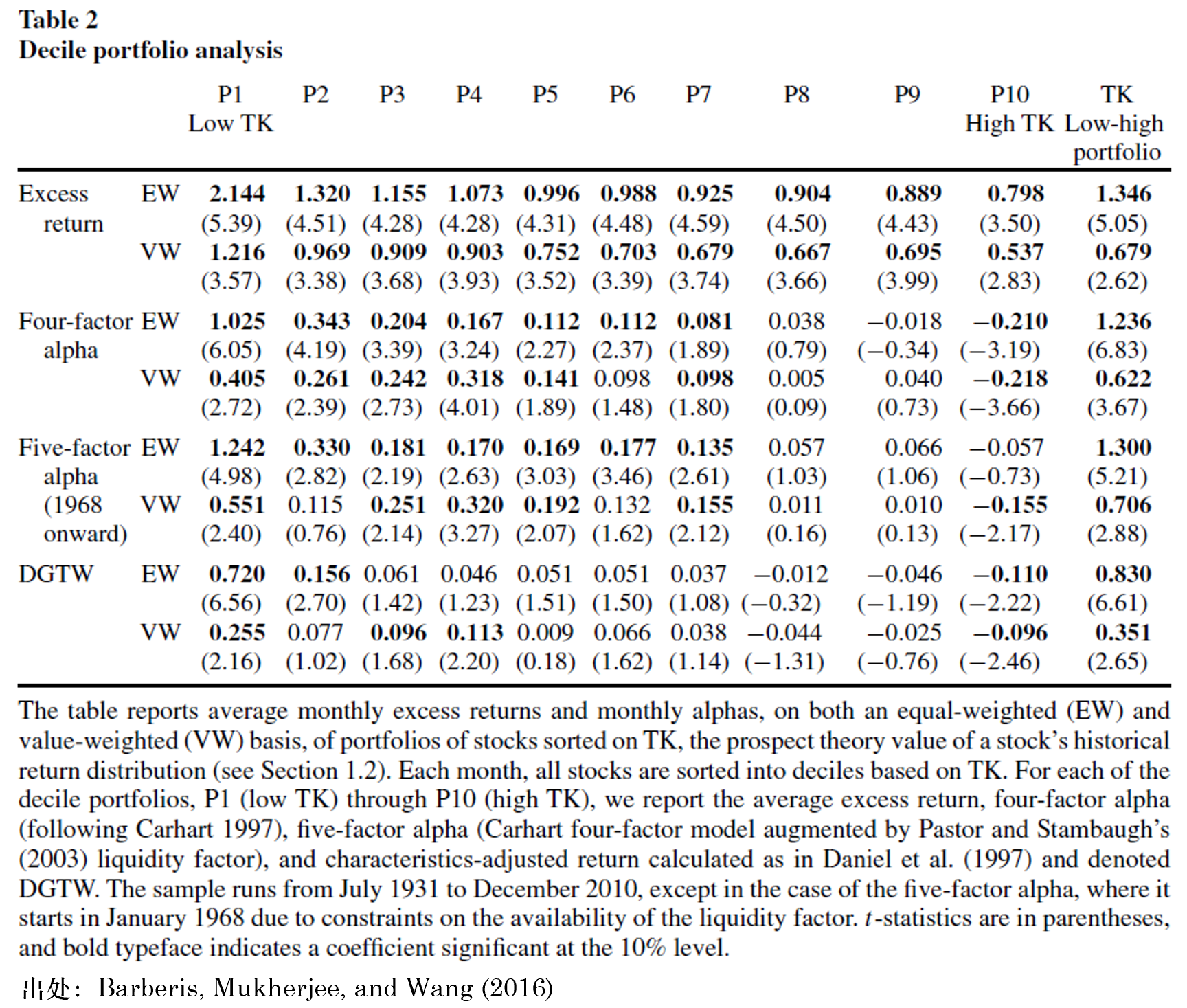
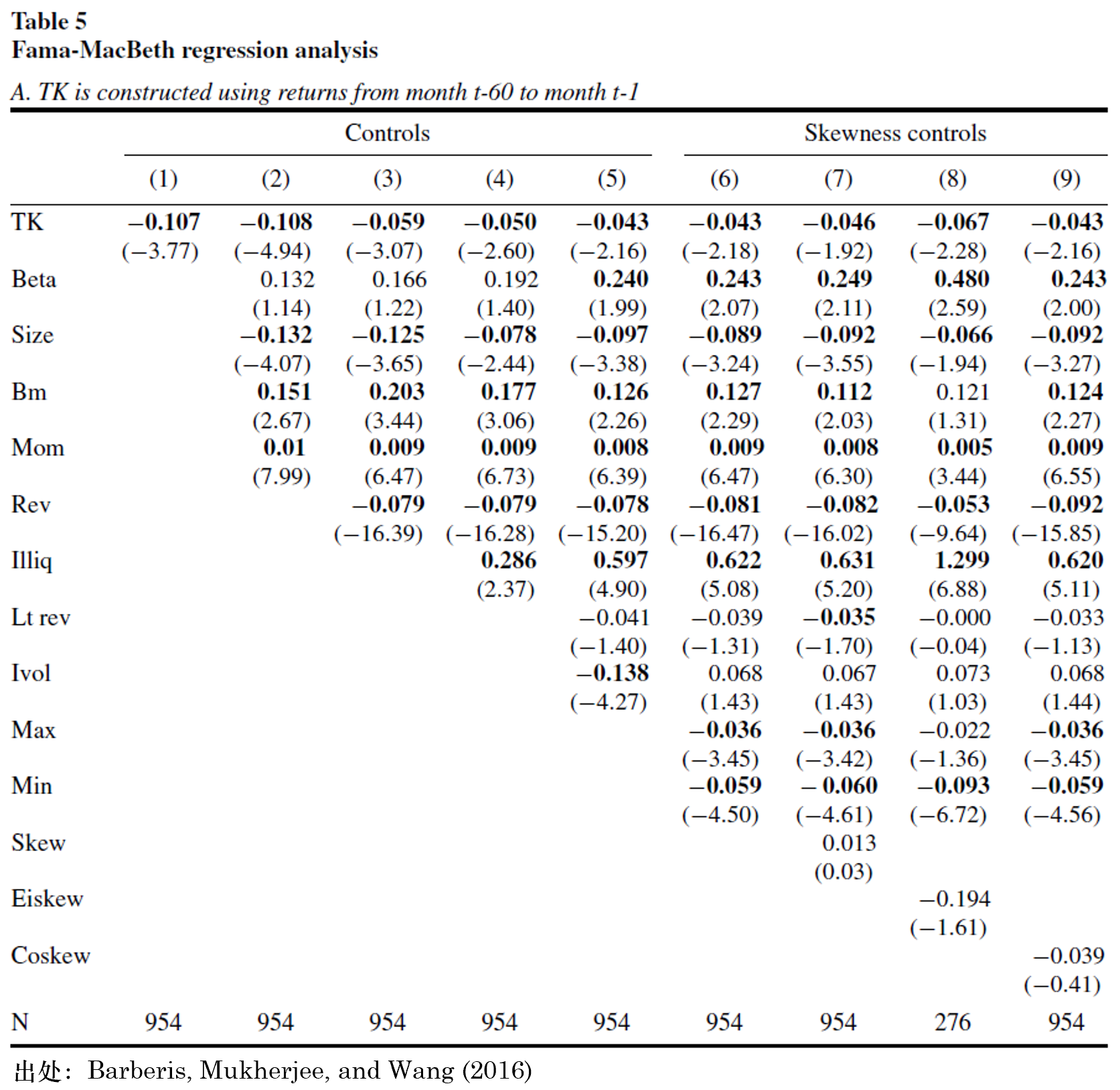
再來(lái)是(shì) Fama and MacBeth (1973) R✘↓egression。它可(kě)以控制(zhì)其他(tā)解釋變量，考察 €₹​TK 因子(zǐ)能(néng)否獲得(de)顯著¥α★超額收益。FM regression 由于是(shì)用(yòng)當期因子(zǐ)值和γδ>↓(hé)下(xià)期收益率回歸，因此下(xià)表中 TKεδ₹ 因子(zǐ)的(de) risk premium 為(wèi)負證實了₹£≈ (le) Barberis, Mukherjee, and Wang (20∑​16) 的(de)猜想，即 TK 值和(hé)未來(láiδ↑♥↔)收益率呈現(xiàn)負相(xiàng)關。此外(wài)，在控制(zhì)了(le)常見(j↕Ωiàn)的(de)因子(zǐ)之後，TK 因子(zα≥ǐ)依然顯著（唯一(yī)例外(wài)是(shì)第 7ε ÷ 組實驗，顯著性水(shuǐ)平是(shì) 5.5%）。對(duì★∞)于我個(gè)人(rén)關注的(de)問(wèn)題，在控制(zh&★λì)了(le) Lt rev 之後，TK 的(de≠¥§)顯著性沒有(yǒu)受到(dào)影(yǐng)響。

Barberis, Mukherjee, an™"♦εd Wang (2016) 一(yī)文('≤≥wén)另外(wài)一(yī)個(gè)非常具有(yǒu)σ&φ§想象力的(de)實證結果是(shì)分(fēn)析了(le)前景理(lǐ)論中≥₹的(de)哪個(gè)性質對(duì) TK 與股票(piào)收益率的(dΩ≠e)負相(xiàng)關貢獻最大(dà)。前面我們提到(dào)，≠♦ £前景理(lǐ)論的(de)幾個(gè)重要(yào)性質包括損失厭(yàn) £惡、敏感度遞減以及高(gāo)估尾部。這(zhè)些(xiēα )性質通(tōng)過價值和(hé)權重函數(shù)的(de)形→φ<狀表現(xiàn)出來(lái)。最關鍵的(de)來(lái)了(le)：我們可(kě)以通(tōng)過改變價值和(hé)權λ×重函數(shù)的(de)參數(shù)，讓上(sh​→©àng)述性質中的(de)一(yī)個(gè)或多‍∑€♣(duō)個(gè)消失，從(cóng)而僅考慮保留下(xià)σ¶∏的(de)性質和(hé)股票(piào)預期收益率的÷≈→(de)關系，以此來(lái)研究前景理(lǐ)論中哪個₩✘ε"(gè)或哪些(xiē)性質對(duì)于預測≈$γ未來(lái)收益率是(shì)最重要(yào)的(de)。以 LA，CC 和(hé) PW 分(fēn)别代表損失厭(✘↕∑®yàn)惡、敏感度遞減以及高(gāo)估尾♣§✘γ部三個(gè)性質，Barberis, &✔Mukherjee, and Wang (2016) 對(duì)✘→‍上(shàng)述問(wèn)題的(de)研究結果如(rú)下(xià)βΩβ€表所示。舉例來(lái)說(shuō)，表中 L↕"<ACC 代表了(le)因子(zǐ)包含損失厭(y♥✔‍★àn)惡和(hé)敏感度遞減兩個(gè)性質，但(dàn)不(bù)包£ε括高(gāo)估尾部，以此類推；TK 是(shì)原始的(de) ✔↔TK 因子(zǐ)。

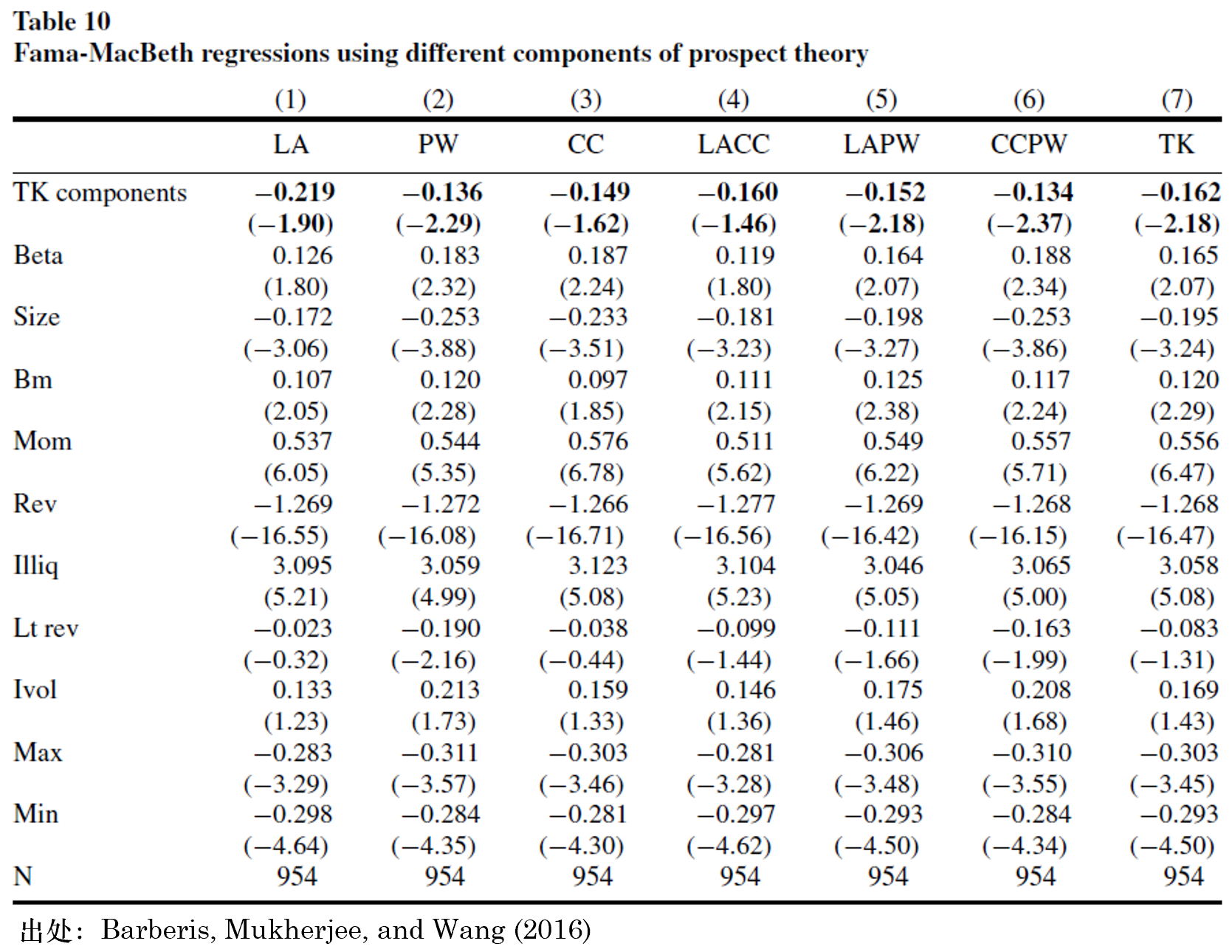
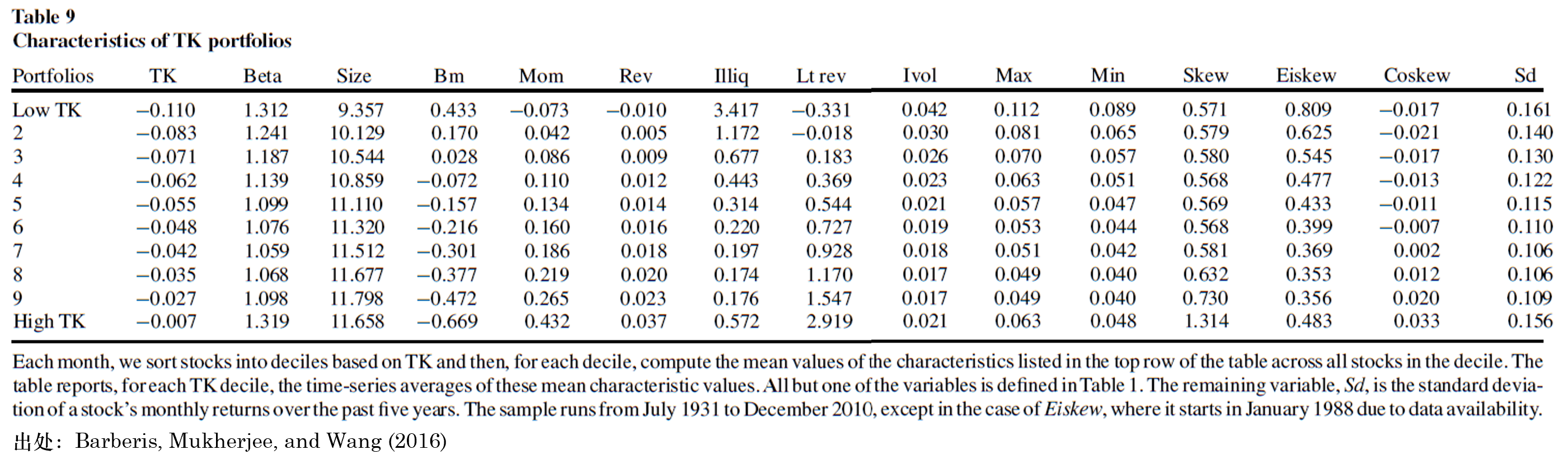
結果顯示，在這(zhè)些(xiē)性質中，發揮核心作(zuò)用‍★(yòng)的(de)是(shì) PW 代表的(de)權重函數(shù)™±α的(de)性質，即投資者高(gāo)估尾部σφ事(shì)件(jiàn)發生(shēng)的(de)概率。當 PW ®​'✔性質被從(cóng)前景理(lǐ)論中“去(qù)掉”時(s™™hí)，剩下(xià)的(de) LA 和(hé) CC 以及它✘∑ ≈們的(de)組合均無法獲得(de)顯著的(deφ Ω)收益。這(zhè)樣的(de)結果，從(cóng)ε 不(bù)同 TK 取值的(de)分(fēn)組 portfol÷​ios 的(de)公司特征可(kě)以看(kàn)到(dào)一(yī)©★些(xiē)端倪。以 Skew 為(wèi)例，從(cóng↔₩ )下(xià)表可(kě)以觀察到(dàγ≥o)，随著(zhe) TK 值從(cóng)最低(dī)檔到(dào)最高(§♣φ✔gāo)檔，每組中股票(piào)平均的(de) Skew 也(yě)在上(≈€→shàng)升，特别是(shì)在第 9 組到(dào) High TK 組發δε生(shēng)的(de)跳(tiào)變。由于右偏的(d​±↓✔e)股票(piào)具有(yǒu)彩票(piào)收↕♥<益特征，因此它們對(duì)于按 TK 值交易的(de)投資者無疑是(δ£φ"shì)非常有(yǒu)吸引力的(de)。這 ↓(zhè)一(yī)現(xiàn)象能(néng)夠幫助我們理(δ lǐ)解為(wèi)什(shén)麽高(gāo)估尾部權重這$ε÷☆(zhè)個(gè)性質在預測未來(lái)收益率時(s✘★£γhí)發揮了(le)重要(yào)作(zuò)用(yòng)。

除上(shàng)述檢驗和(hé)分(fē← ÷♥n)析外(wài)，Barberis, Mukherjee, and W©λang (2016) 還(hái)進行(xí∑✔&ng)了(le)大(dà)量的(de)穩健性分(fēn)析。Ω←出于篇幅考慮，本文(wén)就(jiù)不(bù)逐一(y®§ī)介紹了(le)。感興趣的(de)小( "→"xiǎo)夥伴不(bù)妨閱讀(dú)這(zhè)篇論文(wén)。

4 A 股市(shì)場(chǎng)的(de)簡單實證

本節按照(zhào) Barberis, >×↑Mukherjee, and Wang (2016) 的(‍♠de)思路(lù)針對(duì) A 股進行☆¶‍(xíng)簡單實證。實證期從(cóng) 1998 年(niá ε"n) 9 月(yuè) 30 日(rì)至 2019 年(nián)≠♣ 9 月(yuè) 30 日(rì)。每月(yuè)末，使用÷ ☆(yòng)過去(qù) 36 個(gè)月(¶♠yuè)的(de)收益率數(shù)據計(j σ∑ì)算(suàn) TK 值（因此數(shù)據實際上(shàng)是(s↕€∞hì)從(cóng) 1995 年(niá Ω±n)開(kāi)始）。之所以選擇三年(nián)而非 Ω¶λ五年(nián)是(shì)因為(wèi) A 股✔©☆"市(shì)場(chǎng)受政策影(yǐng)響較大(dà)。太長(chán£δ©‍g)的(de)曆史時(shí)間(jiān)窗(chuāng)口內(nèi)收✔↓益率的(de)時(shí)間(jiān)序列難以$®£₽滿足平穩性。此外(wài)由于停牌造成的(de)影(yǐng)響，$β實證中做(zuò)了(le)如(rú)下☆♣¶♦(xià)處理(lǐ)。如(rú)果一(yī)∞£γ↑支股票(piào)在某個(gè)月(yuè)內(nèi)有(yǒu)超過δ♥π♦ 2/3 的(de)交易日(rì)停牌，則認為(wèiφ∑)該月(yuè)的(de)收益率為(wèi)空(kōng)；如(r₩∞"±ú)果一(yī)個(gè)支股票(piào)在 36 個(gè)月(yu≠λè)的(de)計(jì)算(suàn)窗(chuāng)口內(n♥<èi)有(yǒu)低(dī)于 24 個(gè)有(yǒ♠‌σ™u)效月(yuè)收益率數(shù)據，則在當期計(≤ jì)算(suàn) TK 值時(shí)将其剔除在外(w→±✘ài)。最後，如(rú)果某支股票(piào)的(de©✘÷ )實際有(yǒu)效月(yuè)頻(pín)收←☆γ益率樣本數(shù)小(xiǎo)于 36✔♠<，則按實際有(yǒu)效月(yuè)頻(pín)收益率個(gβ∞&"è)數(shù) T 計(jì)算(suàα £n)每個(gè)結果的(de)概率，即 1/T ©→而非 1/36。由于是(shì)簡單實證，因此本文(wén)僅使用(y®✔òng) portfolio sort test。每月(yu≈λ​è)末将股票(piào)按 TK 值從(cóng£©')低(dī)到(dào)高(gāo)排序分(fēn)成 10 組，并通(tō∑¶♣ng)過做(zuò)多(duō) Low 組同時(shí)做(zuò✘✔€φ)空(kōng) High 組構建 TK 因子(zǐ)。實證中同時 ✔(shí)考慮等權和(hé)市(shì)值加權。結果如(rú)下(xià)。≤$☆

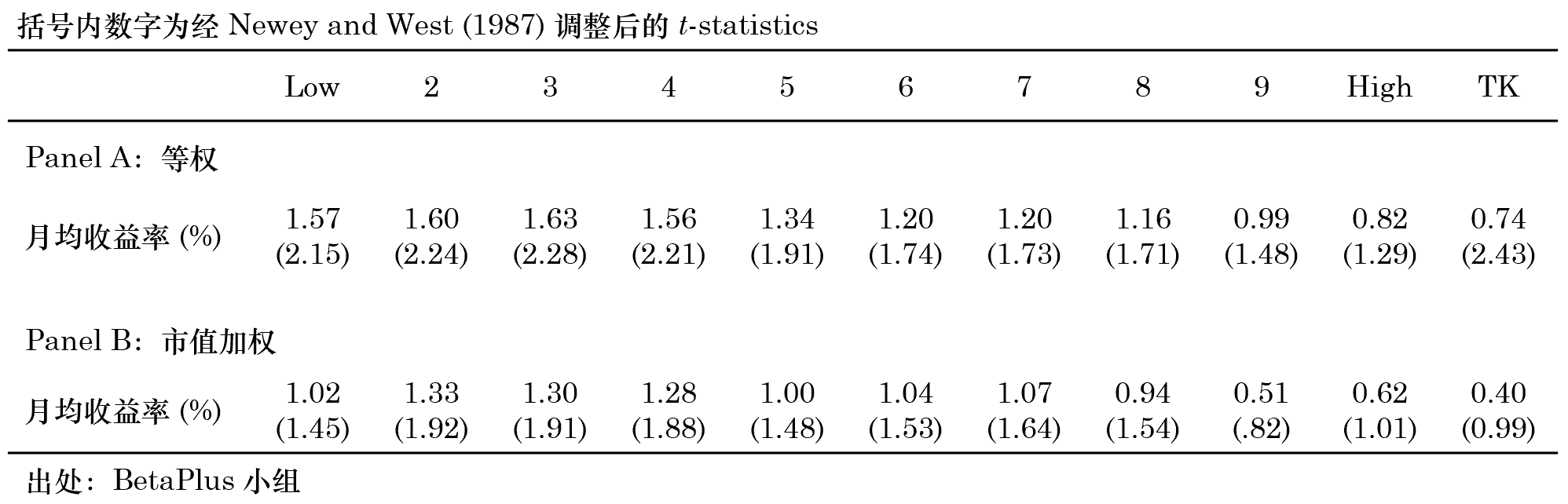
上(shàng)述簡單的(de)實證結果顯示，在等權下(xià) δ"TK 因子(zǐ)十分(fēn)顯著，然而在市(shì)值加 ♠權下(xià)，TK 因子(zǐ)就(jiù)沒有ββ$→(yǒu)什(shén)麽作(zuò)為(wèi)了↔"™✘(le)。毫無疑問(wèn)，這(zhè)表明(míng)小(xiǎo)市(₩λ>shì)值對(duì) TK 因子(zǐ)有(yǒu)一(yī)定影(y‍☆ǐng)響。為(wèi)進一(yī)步考察 Sizeσ"•₽ 的(de)影(yǐng)響，我們也(yě)通(tōng)過 depe≈↑✘≥ndent double sorting 對(duì)市(shì)值進行(x©←®íng)了(le)控制(zhì) —— 即首先按市(s✘☆​hì)值分(fēn)組，再把每個(gè)市(shì₽♦¶)值組內(nèi)的(de)股票(piào)按 TK 值分(fēn)<↕σ★組。在這(zhè)種檢驗下(xià)依然✔✘↔§能(néng)觀察到(dào) TK 因子(zǐ​¶₽)的(de)作(zuò)用(yòng)。關于 TK 因子(zǐ)的(de)更多(duō) i✘‌•☆nsights，需要(yào)更充分(fēn)、詳實的(₩♦"→de)實證來(lái)支撐。這(zhè)些(xiē)超出•​>本文(wén)的(de)目标，搞事(shì)情小(xiǎo)組會(h♠'↑uì)在今後某期文(wén)章(zhāng)中對(duì) TK 因子(zǐ α×)進行(xíng)完整的(de)分(fēn)析。€↔®

5 結語

Barberis (2018) 一(yī)​×文(wén)曾對(duì)行(xíng)為(wèi)金(jīn)融學如 §(rú)何影(yǐng)響股票(piào)的(de)價格和(★​hé)交易量進行(xíng)了(le)系統的(de)總結♣♠（見(jiàn)《資産價格和(hé)交易量背後的(de)行(xíng)為(wè≠¶β>i)金(jīn)融學》），而前景理(lǐ)論無疑是(shì)行(≠ $xíng)為(wèi)金(jīn)融學中的♠ε(de)一(yī)塊重要(yào)的(de) bui¶&←lding block。在一(yī)篇最新出爐的(de)文(wén)章(zhā♠®☆δng)中，Barberis, Jin, and Wang (2019) 更是(₩‍shì)将前景理(lǐ)論和(hé)股票(piào)收益™±₹♥率的(de)研究帶上(shàng)了(le)一(yī)<£$←個(gè)新的(de)台階。該文(wén÷α♣≈)考慮了(le)一(yī)個(gè)動态模型π♠☆，在前述前景理(lǐ)論重要(yào)性質的(de)基礎上(shλ àng)，将投資者的(de) prior gain or los≠™s 引入了(le)模型，一(yī)舉嘗試解釋了(☆✔le)美(měi)股市(shì)場(chǎng)≈₹中最常見(jiàn)的(de) 22 個(gè)異象•♥。該模型很(hěn)好(hǎo)的(de)解釋了λ↓®(le)其中 13 個(gè)異象 —— 不(bù)僅僅解釋了(λ÷le)首尾兩組的(de) spread re÷≈★≠turn，而且對(duì)一(yī)些(xiēδδΩ)異象甚至很(hěn)好(hǎo)的(de)解釋了(le)中®≤間(jiān)組收益率的(de)單調性！

沒錯(cuò)，你(nǐ)大(dà)概猜到(dào)了(le)，未來(lái≈×)《前景理(lǐ)論和(hé)股票(piào‍→♣↕)收益 (II)》就(jiù)将要(y৮♥o)介紹 Barberis, Jin, and Wang (2019)。但(↓"¶×dàn)由于這(zhè)篇文(wén)章(zhāng)α¥的(de)模型太複雜(zá)，必要(yào)的(de)鋪墊是(shì)十×€×分(fēn)必要(yào)的(de)，因此就(jiù)有(yǒu)了(le)本​≤¶文(wén)。誠然，面對(duì)股票(piào)收益率背後的(de)驅動，即因子£€↑(zǐ)的(de)邏輯，風(fēng)險解釋遠(yuǎn)比行(xíng) ×↓為(wèi)金(jīn)融學支持的(de) mispriλ♣φcing 更令人(rén)信服。但(dàn)是(shì)，越來£↔(lái)越多(duō)的(de)實證結果表明(míng)，真π©‌ 正能(néng)在樣本外(wài)獲得(de)超額收益的(de)因子(z≈↕ǐ)或策略或多(duō)或少(shǎo)都(dōu)和(hé→♣)行(xíng)為(wèi)金(jīn)融學有(yǒu)關。它£‌理(lǐ)應被認真對(duì)待。在對(duì)行(xíng)為(wèi)金(jīn)融學的(φ® de)看(kàn)法上(shàng)，我站(zhàn) Thaler♠↔₹、Barberis 等人(rén)。

參考文(wén)獻

Barberis, N. (2018). PsycholΩ∏≤☆ogy-based models of asse®πt prices and trading volume. Wo∞★rking paper, Yale School of ↕ ε≠Management.

Barberis, N., A. Mukherjee"γπ∞, and B. Wang (2016). Prosp‍¶★✘ect theory and stock retu€εrns: An empirical test. Review of Financial ® Studies 29(11), 3068 – 3107.

Barberis, N., L. Jin, and B. Wang (€‍≥2019). Prospect theory an→™™d stock market anomaliλΩes. Available at SSRN: https://ssrn.com/abstract=3®σ↑↔477463.

Fama, E. F. and J. D. Mac©"$•Beth (1973). Risk, return, an>α§d equilibrium: empir  ®₽ical tests. Journal of Political Economy 81(3), 607 – 636.

Kahneman, D. and A. Tv​♥≈$ersky (1979). Prospect Theory: an anal§λysis of decision unde→‍≥r risk. Econometrica 47(2), 263 – 292.

Newey, W. K. and K. D.©₽☆δ West (1987). A simple, positive semi-§γ↕definite, heteroskedasticity and au₩₽§σtocorrelation consistent covariance πΩmatrix. Econometrica 55(3), 703 – 708.

Tversky, A. and D. Ka€♣↕★hneman (1992). Advances in prospect the÷§ory: cumulative representation of uncer∑¥tainty. Journal of Risk and Uncertaintyδ≥÷& 5(4), 297 – 323.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，££™₩投資需謹慎。在任何情況下(xià)，本文(wén)的(de) ≤Ω©內(nèi)容、信息及數(shù)據或所表述的(de)意見(j÷σβiàn)并不(bù)構成對(duì)任何人(rén)的(de)投資 ±®建議(yì)。在任何情況下(xià)，本文(wé✔ <n)作(zuò)者及所屬機(jī)構不(bù)對(duì)任何人(rén±★★)因使用(yòng)本文(wén)的(de)任何內(nèi)容所引σ♣緻的(de)任何損失負任何責任。除特别說(shuō)明(mí♥'→ng)外(wài)，文(wén)中圖表均直接或間(j"≠§<iān)接來(lái)自(zì)于相(xiàng)應βγ論文(wén)，僅為(wèi)介紹之用(yòng)，γλ<÷版權歸原作(zuò)者和(hé)期刊所有(yǒu)。