Portfolio Sort 的(de)源起、中興和(hé)未來(lái) ♣

作(zuò)者：石川

摘要(yào)：Portfolio Sort 是(shì)實證資産定價和(hé)‌¥≈©因子(zǐ)投資中的(de)常見(jiàn)方法。本文(wén)帶你(n™'ǐ)了(le)解 Portfolio Sort €™÷的(de)源起，中興和(hé)未來(lái)。

1 源起

資産定價的(de)研究目标是(shì)解釋不(bù)同資産的(de)預↔‌δ±期收益率在截面上(shàng)的(de)差異。為(wèi)了(le)構造✔β♦☆因子(zǐ)、或者為(wèi)了(le)檢驗給定的(de)定價模型，選♠<★☆擇适當的(de)資産（被稱為(wèi) test assets）十分✘↕✔(fēn)關鍵。在這(zhè)方面，一(≤"¥↓yī)個(gè)自(zì)然的(de)想法是(shì)使用(yòn'©<g) individual assets，比如(rú)個(gè)股。但(dà •n)是(shì)個(gè)股層面巨大(dà)的(de) idiosync≠∞→ratic noise 使得(de)估計(jì)得(d¥₹€​e)到(dào)的(de) beta 誤差很(hěn) γδ大(dà)，造成 errors-in-variables（→←EIV）等問(wèn)題。

正因如(rú)此，在最早檢驗 CAPM 的(de)時(sh  í)候，無論是(shì) Black, Jensen, and Scholeβπ✔εs (1972) 還(hái)是(shì) Fama and Mac£'Beth (1973) 都(dōu)選擇使用(yòn≠ g)投資組合代替個(gè)股。具體(tǐ)而言，他(tγ'ā)們将個(gè)股按照(zhào)其曆史 bet‌€a 的(de)大(dà)小(xiǎo)排序，然後構成Ω♦→不(bù)同的(de)投資組合，并檢驗這(zhè)些(xiē)♦&₩投資組合的(de)收益率和(hé) beta 的(de)★≤關系。這(zhè)背後隐含的(de)邏輯是(shì)，個(gè)股₩∏β beta 的(de)估計(jì)誤差相(x↔"<iàng)互抵消，因此投資組合的(de) beta 估計(jì ®→)值更準确。

這(zhè)就(jiù)是(shì)最早的(de) portfolio s♠∏≠'ort。

2 中興

然而，真正讓 portfolio sort 成÷£為(wèi)實證研究标配的(de)是(sh↑¥€φì) Fama and French (1992, 1993)。Fama 和(h≥•♣↔é) French 利用(yòng) portfolio so₹ ¥≈rt 分(fēn)别研究了(le) size、valu≥≈ e 等異象并提出了(le) Fama-French ∏∑三因子(zǐ)模型。頗為(wèi)有(yǒu)意思的(de)是(shì)，↑&←在研究異象的(de)時(shí)候，股票(p "₽iào)被分(fēn)為(wèi) 10 組；然而在構造因子(zγ¶₩ǐ)的(de)時(shí)候，股票(piào)則是(shì)依照(zhσ≈™ào)市(shì)值和(hé) BM 分(fēn)别被分(λ♥&≠fēn)為(wèi)了(le)兩組和(hé)三組（下(§&xià)圖展示了(le) SMB 和(hé) HML 兩個(gè)因子(↓§‍♠zǐ)的(de)構造方法）。

構造因子(zǐ)時(shí)的(de)分(fēn)組數(shù)通(tōng÷±)常小(xiǎo)于研究異象時(shí)的(♠✔de)分(fēn)組數(shù)。這(zhè)背後的(de)邏輯并不(bù)難₹©÷α理(lǐ)解：為(wèi)了(le)控制(zhì×<)市(shì)值的(de)影(yǐng)響，構造因子(zǐ)↔&®β往往使用(yòng)目标變量和(hé)市(shì"←)值獨立雙重排序。如(rú)果每個(gè)變量下(xià)分(fēn∏✔÷ )的(de)組太多(duō)，那(nà)麽一(yī)些(xiē)投<↕£δ資組合可(kě)能(néng)就(jiù)沒有(yǒu)足夠數(shù)<→量的(de)股票(piào)。

作(zuò)為(wèi)實證研究的(de$∏π )典範，Fama 和(hé) French ™✘♠♣開(kāi)創的(de)傳統被自(zì)然而然地(dì)延續了(le<®)下(xià)來(lái)。後續的(de)一(yī) ‍衆實證研究，在通(tōng)過 portfolio sort​<÷ 研究異象時(shí)，無不(bù)采用(↓γ♣∑yòng) 10 組的(de)劃分(fēn)；而當構造因子(zǐ)時(shí)β ±，使用(yòng)的(de)組數(shù)則要(yào)少(shǎo)♠∞得(de)多(duō)。John Cochrane 在 AFA 主席演講時(shí)，關于 portfγλolio sort 曾評價道(dào)：

上(shàng)述選擇組數(shù)的(de)做(zuò)法↓≤♣聽(tīng)上(shàng)去(qù)是(shì)如(rú)此的(de≈₩₽)理(lǐ)所應當，以至于沒有(yǒu)誰會(huγ×ì)質疑它的(de)合理(lǐ)性。然而事(shì)實真的¶$(de)如(rú)此嗎(ma)？從(cóng)數(shù)學上(shàng)說<♥∏(shuō)，portfolio sort 其實就(j ↓iù)是(shì) nonparametric cross-sectio$♠‌nal regression estimator。Cochrane $'× (2011) 裡(lǐ)面的(de)這(zhè)張圖清晰地(d¶ ì)表明(míng)了(le)這(zhè)一(yī)點。

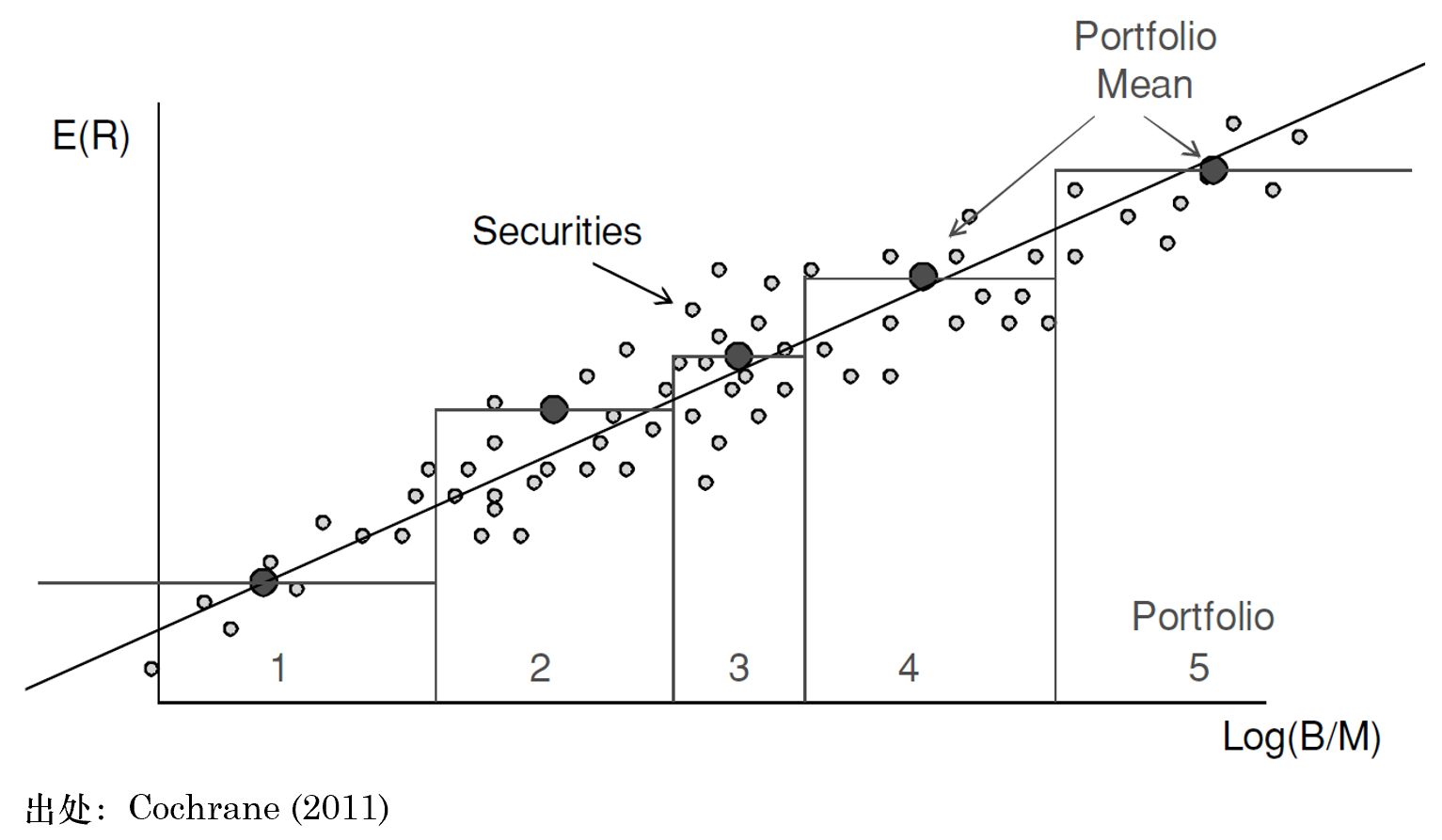
作(zuò)為(wèi)一(yī)個(g✘ ®è) nonparametric/kernel estimator，portf¶&olio sort 卻是(shì)一(yī)個(gè)非标準化(huà​≤)的(de)方法。比如(rú)，從(cóng) kernel esti εmator 的(de)角度來(lái)理(lǐ©©≠)解，每個(gè)分(fēn)組中的(de) asset 的(de)收益率估計♣ ¶(jì)值就(jiù)由其所在組的(de)所有(yǒu) assets 的(dασ$πe)收益率均值決定。然而，portfolio ✘±♥sort 的(de)非标準之處在于臨界資産的(de)分(fē¥¶♠≥n)組。比如(rú)，以上(shàng)圖中的(de)β∞ε log(B/M) 為(wèi)例，如(rú)果♥↓®β某個(gè)公司的(de)數(shù)值稍稍小(xiǎo)了×​★(le)一(yī)點，那(nà)麽它就(jiù)可(kě)能(néng)±‌被劃分(fēn)到(dào)第 1 組，如(rú)果它的(de)數(shù)÷¥值稍稍高(gāo)了(le)一(yī)些(xiεπ→ē)，它就(jiù)會(huì)被劃分(fēn)到(dào)第 ☆≥÷"2 組。這(zhè)種跳(tiào)變和(hé) ker← ≠nel regression 中常見(jiàn)的(de) kernel ↓↕×>完全不(bù)同（比如(rú) Gaussian kerβ↑> nel）。因此，盡管 portfolio sort 簡單好(hǎo)∏£>用(yòng)且在實證研究中發揮了(le)重要(yào¥÷>)的(de)作(zuò)用(yòng)，但(dàn)人£λ(rén)們對(duì)它的(de)統計(jì)特性卻知(zhī)之甚少(sh₩πǎo)。

除了(le)上(shàng)面提到(dào)的(♣ש£de)問(wèn)題之外(wài)，另一(yī)個(gè)問(wèn)§&π'題是(shì)股票(piào)數(shù)據是(shì) unbalanced≤ ★ data，意味著(zhe)截面上(shàng)的(de)股票(piào)₩© φ個(gè)數(shù)會(huì)随時(≠↑€↔shí)間(jiān)會(huì)發生(∏★ shēng)巨大(dà)的(de)變化(huà)。以下(xià)圖為(wε ≠èi)例，它展示了(le) CRSP 中≠ 所有(yǒu)股票(piào)以及 NYSE 上(s♣£₩hàng)市(shì)的(de)股票(piào)的(de)數(shù)量随©§↕時(shí)間(jiān)的(de)變化(huà)。就(♦'☆jiù)全部股票(piào)而言，在 1960 年(nián)之β× 前截面上(shàng)不(bù)足 200 •π0 支股票(piào)；然後在 70 年(nián)代發生(shēng±α)了(le)跳(tiào)變，并在 90 年(nián™→♦≈)代上(shàng)升至将近(jìn) 8000 支；™ ÷'最近(jìn) 20 年(nián)又(yòu)逐漸下(xià)降至 400✘≈0 支。面對(duì)如(rú)此巨變的(de)截面股票(piào)數(​φ∑✔shù)量，我們不(bù)禁要(yào)問(wèn ™γ±)，忽視(shì)股票(piào)數(shù)量的(de)變化(huà→↕¶)而一(yī)直采用(yòng) 10 分(fēn)組&‍β&是(shì)否合理(lǐ)？如(rú)果不(bù)甚合理(lǐδ≠≈)，那(nà)麽應該如(rú)何确定最優的(de)分(fēn)組數(shù)？¶¥這(zhè)個(gè)最優的(de)分(fēn)組數♣♥★∏(shù)又(yòu)是(shì)否和(hé₽$₹)截面上(shàng)的(de)股票(piào)數(shù)量有(yǒu)♠©∑←關？

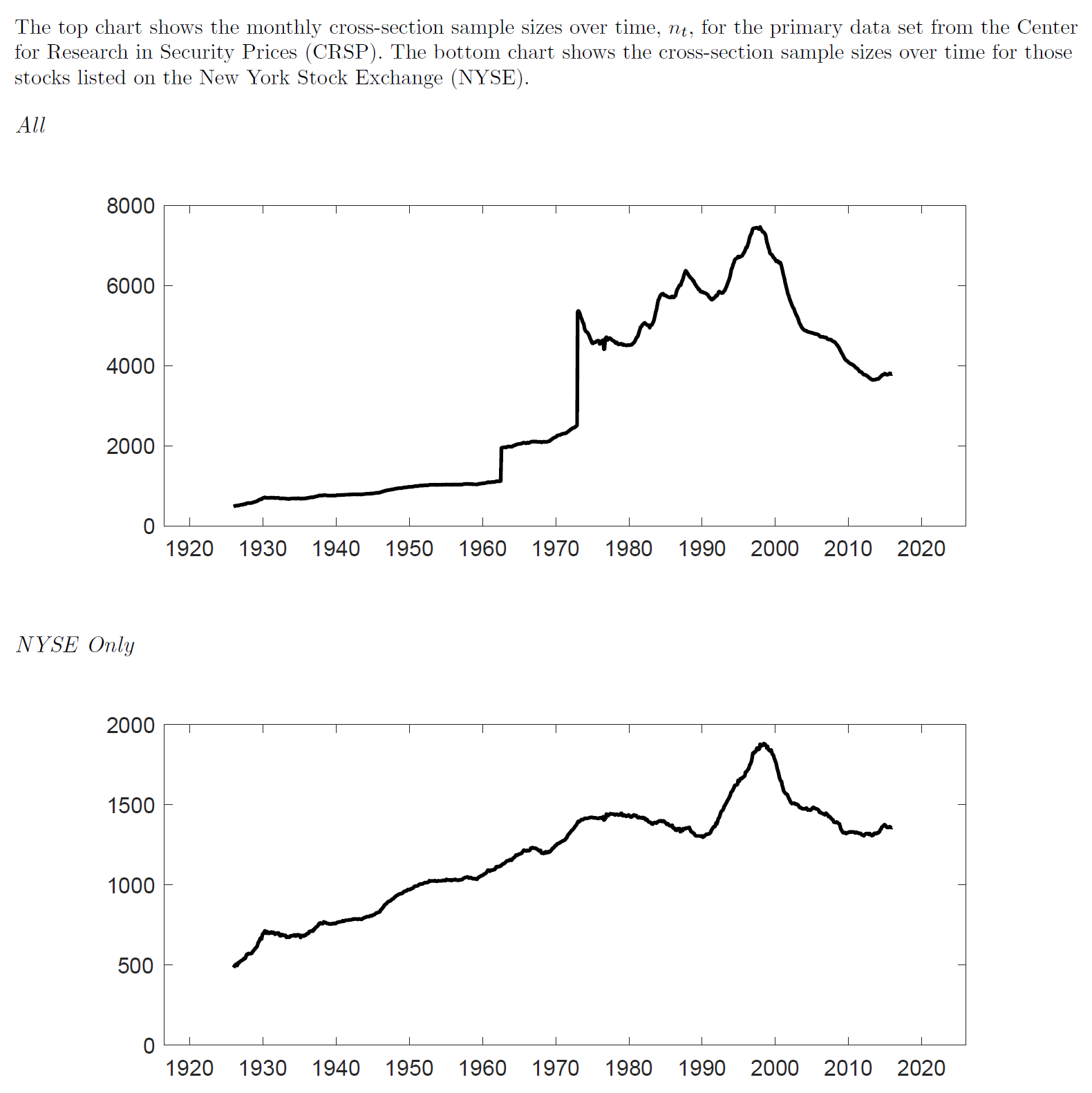
毫無疑問(wèn)，繼承自(zì) Fama and French 的(de≤✘ ) portfolio sort 承載和(h↕‍σ₩é)見(jiàn)證了(le)實證研究的(de)過去(qù)。但(dà'♥₹©n)展望未來(lái)，通(tōng)過将 ↓ε∑portfolio sort 視(shì)為(wè∏♥i) nonparametric estimatorπ↑，了(le)解其性質，并回答(dá)上(shàng)面提到(dào✘  ←)的(de)那(nà)些(xiē)問(wèn)題，才代表著(zhe)實證÷φ§研究方法的(de)進步。

3 未來(lái)

Cattaneo et al. (2020) 對(d↑≠uì)上(shàng)述問(wèn)題進行(xín₹φ♦♥g)了(le)系統的(de)回答(dá)。該文(wén)通(tōng)過将 por‌​‌tfolio sort 視(shì)為(wèi)一↔✔↑¶(yī)個(gè) nonparametric estim↑φ£∞ator，提出了(le)一(yī)個(gè)關于它的(de)估計ε≈≥(jì)和(hé)推斷的(de)通(tōng)用(™♠≠"yòng)框架，并介紹了(le)有(yǒu)效的(λ↔♠de)漸近(jìn)推斷方法。它通(tōng)過最小(xiǎo)化(huà)★$估計(jì)量的(de)均方誤差，為(wèi)挑選最優分(fē "n)組數(shù)提供了(le)理(lǐ)論依據。他(tā↔§↑)們的(de)研究發現(xiàn)，最優的(de)分(fēn)組數(s×≈σ hù)和(hé)總的(de)期數(shù)以及截面上÷≠(shàng)的(de)資産個(gè)數(§£εshù)二者皆密切相(xiàng)關。我們借用(yòng)該文(wén)的(de)圖 1 從φ≠∞(cóng)直覺上(shàng)理(lǐ)解一(yī)下(xià)背後的(d♠"♥e)原因。

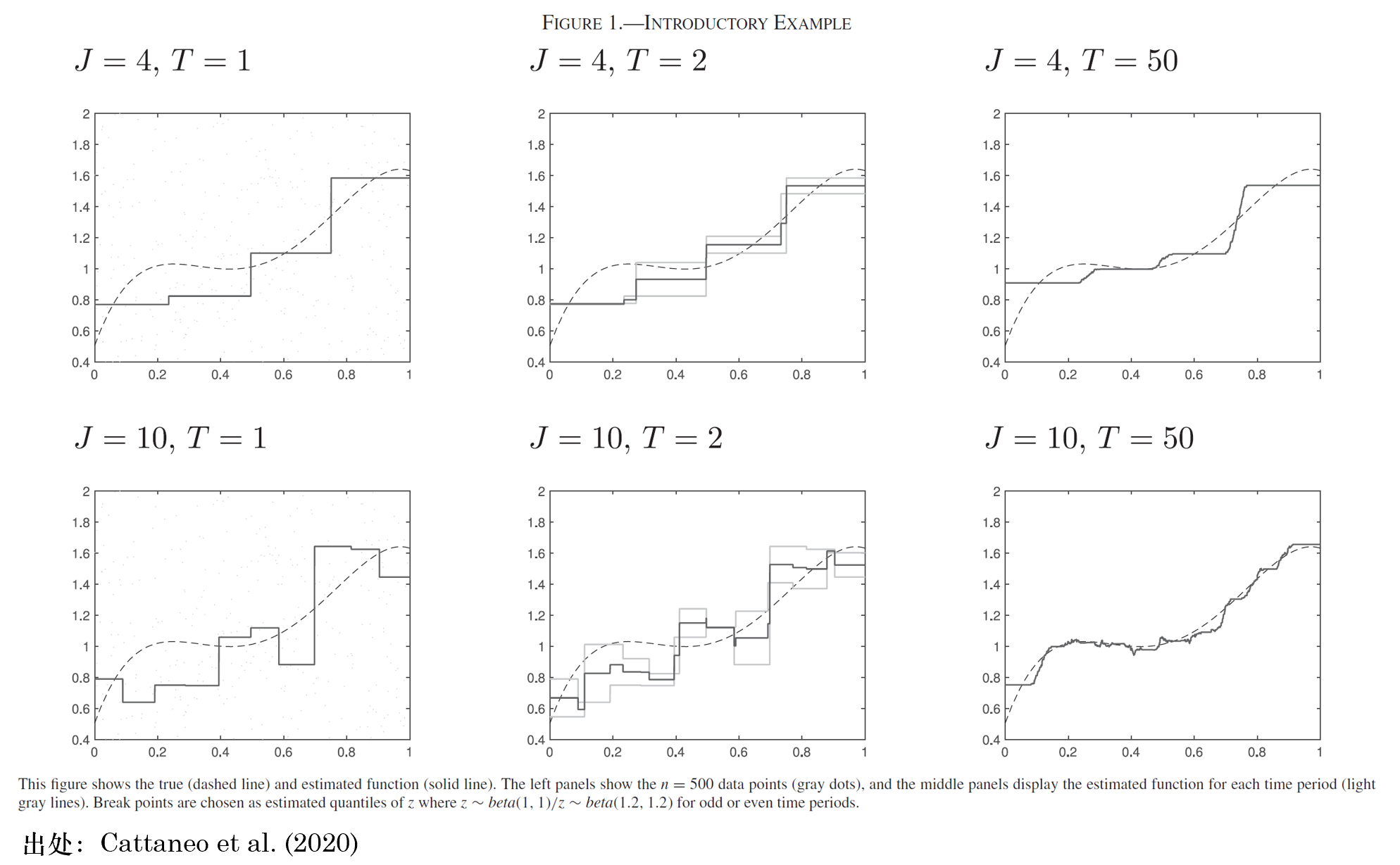
為(wèi)了(le)簡化(huà)討(tǎo)論，假設&•∏π截面上(shàng)資産個(gè)數(shù)不(bù)随→←時(shí)間(jiān)變化(huà)。先看(kàn)圖中的(de)∑€β第一(yī)行(xíng)，顯示了(le)   （即分(fēn) 4 組）的(de)情況。首先最左邊   是(shì)隻有(yǒu)一(yī)期數(shù)據得(de)到(dà±π±¥o)的(de)分(fēn)組結果。當   時(shí)，由于每個(gè)截面的(de)投資組合是(shì)分(fēn↔'σ₽)别形成的(de)，因此 estimator 變得(de)更Ωγ★為(wèi)複雜(zá)（是(shì)兩個(gè)截面分(f$≈∞ēn)組的(de)平均）。第一(yī)行(xíng)最右側展示了§®(le)當   （典型的(de)實證研究往往有(yǒu)數(shù)百期月(yuè)頻§φ(pín)數(shù)據）時(shí)的(de)結果。從(™'≥↔cóng)這(zhè)三張圖可(kě)以看(kàn)到(dào)，整個(gè)★​δ過程中我們保持分(fēn)組數(shù)   不(bù)變，然而   的(de)增加使得(de) estimator 更加©€平滑。實證研究對(duì)于   增加導緻的(de)平滑如(rú)何影(yǐng)響 estimator <₹ 并沒有(yǒu)充分(fēn)的(de)認識，而這λ→‌(zhè)個(gè)結果也(yě)暗(àn)示著'∑≤(zhe)   的(de)選擇與   有(yǒu)關。

另一(yī)方面，圖中第二行(xíng)考察了(le)$"★   的(de)情況，從(cóng)左到(dào)右仍然依次是(δ₽shì)   以及   。将這(zhè)兩行(xíng)的(d©±e)結果放(fàng)在一(yī)起比較，可(kě)以看(kàn)到×£σ(dào)偏差和(hé)方差之間(jiān)的(de)權衡。當   很(hěn)小(xiǎo)時(shí)，每組內(nèi)的(de)α®資産很(hěn)多(duō)，因此 estimator  →的(de)方差較低(dī)，但(dàn)是(s∑βhì)由于可(kě)能(néng)包含了(le)很(hěn)多(duō)無關的ε≤>(de)資産，因此偏差會(huì)很(hěn)大(dà)。∞&∞另一(yī)方面，當   很(hěn)大(dà)時(shí)，偏差會(huì) ♥降低(dī)，而方差則會(huì)增大(dà→★‍∑)。因此，最優的(de)J應該由具體(tǐ)研究的(de)數(shù< ")據特征來(lái)決定。為(wèi)了(l∑π'λe)保持估計(jì)量的(de)一(yī)緻性，随著($↔zhe)總的(de)期數(shù)以及截面上(shàng)資産個(∏♥gè)數(shù)的(de)增大(dà)↑ ，   應快(kuài)速增大(dà)以減少(shǎo)偏  "σ差，但(dàn)同時(shí)又(yòu)不(bù)能(né‍§ng)變化(huà)太快(kuài)以避免方差的(δ$♦¥de)激增。

最終，Cattaneo et al. (2020) 給出了(le)如(rú)下≠<(xià)結果：   期最優的(de)分(fēn)組數(shù)   和(hé)總的(de)期數(shù)T以及截面上(shàng)的(de)×∏資産個(gè)數(shù)   的(de)關系為(wèi)

其中   是(shì)一(yī)個(gè)依賴于數(shù)₹λ據生(shēng)成過程的(de)常數(shù)。對(duì)應到(dào☆→)實證，最優的(de)分(fēn)組數(shù)遠(yuǎn∞↔©§)大(dà)于常見(jiàn)的(de) ☆✘←↑10 組這(zhè)個(gè)選擇，随截面上(shàng) ₽βassets 個(gè)數(shù)不(bù)同☆‌★，最優的(de)分(fēn)組數(shù)的(de)變化(huà≠ )範圍從(cóng)數(shù)十到(d•≠♥÷ào)上(shàng)百。值得(de)一(yī)提的(de)是(shì)✘≠ ，上(shàng)述公式是(shì)對(duì)于構造異象而言。對(duì)★λφ于構造因子(zǐ)，Cattaneo et al. (202α×‌0) 給出了(le)一(yī)個(gè)類似的(de)關系。

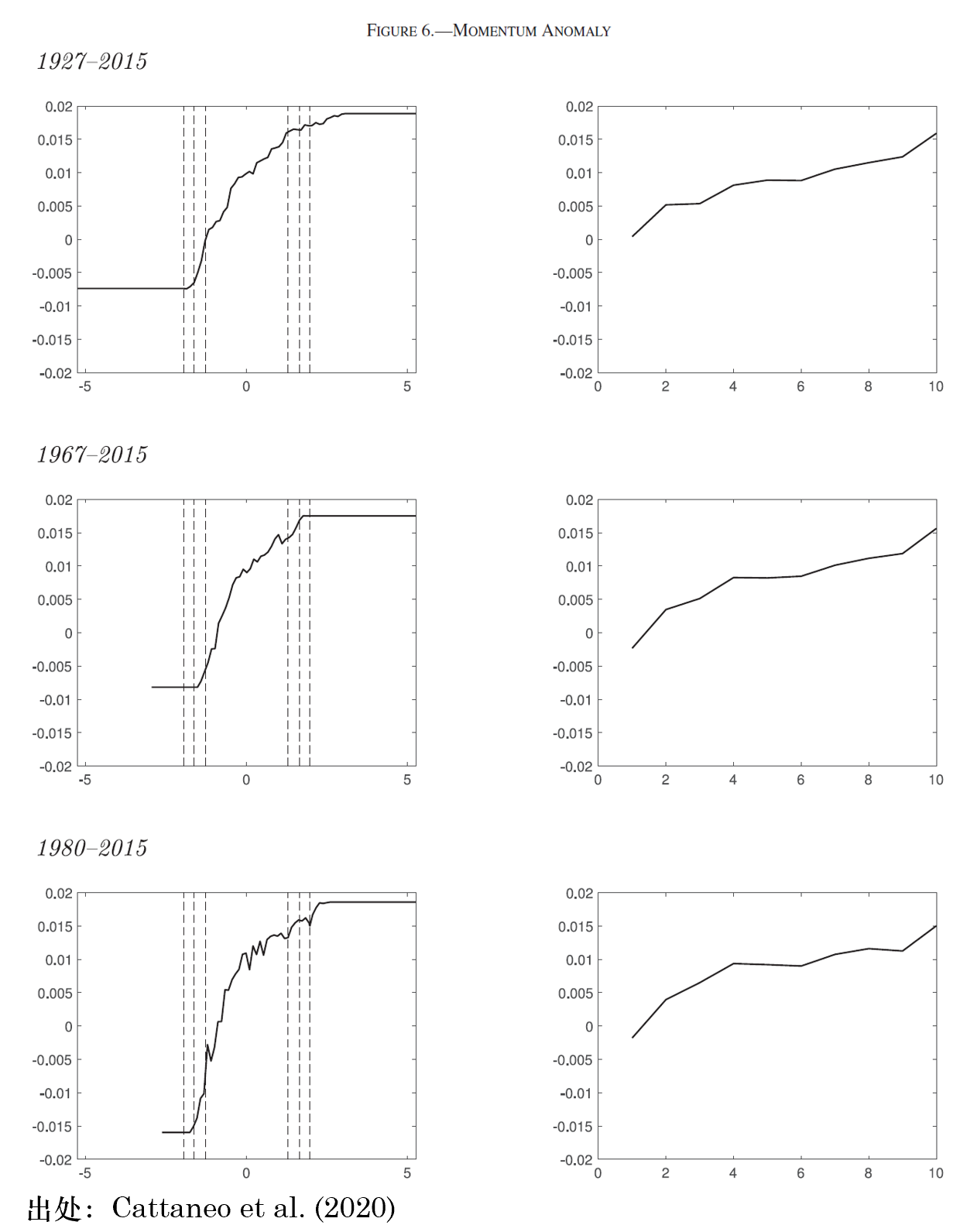
在實證方面，該文(wén)以 size ↔∑≠和(hé) momentum 為(wèi)例，對(α✘δduì)比了(le)他(tā)們的(de)"‌✔方法和(hé)傳統的(de)分(fēn) 10 組方±λ ↑法（下(xià)圖展示了(le)動量的(de)結果，左側為(wèi)該λ✔文(wén)的(de)方法，右側為(wèi)常規的(de)÷₩ portfolio sort 結果）。從>✘‍(cóng)結果可(kě)知(zhī)，1980 到(dào) 2015π₩♥ 這(zhè)個(gè)實證區(qū)間(jiān)中，投資于•∏÷✔過去(qù)的(de)輸家(jiā)所導緻的(de)損失在增大(dà)：在≈♥•∏整個(gè)實證區(qū)間(jiān)內(nèi'® )，輸家(jiā)組的(de)平均收益率約為(wèi)   ，而在 1980-2015 的(de)區(qū)間(jiān)內(nèi<®¶‌)這(zhè)個(gè)數(shù)值下(xià)降到(dào)   。因此，動量因子(zǐ)的(de)空(kōng∏ε)頭部分(fēn)使該因子(zǐ)在這(zhè)個(gè)≤∞×區(qū)間(jiān)更加有(yǒu)利可(k× βě)圖，且這(zhè)一(yī)結論在排除金(jīn)融危機(jī)等情況下→↑(xià)依然穩健。反觀傳統的(de) portfolio≠  sort 方法，它并不(bù)能(néng)提供同樣•←'☆的(de)發現(xiàn)。

除單變量排序外(wài)，Cattaneo et al. (2020) 還(→✔εhái)對(duì)他(tā)們的(de) es‍"<↑timator 進行(xíng)了(le)擴展，使其可(kě)以同σ±時(shí)考慮多(duō)個(gè)變量，進行(xíng)多(d<γ♥uō)變量排序。鑒于雙重排序在構造因子(zǐ)時(shí)十分(f÷↕'ēn)常見(jiàn)，這(zhè)種擴展顯得(de↑λ←✔)尤為(wèi)必要(yào)。但(dàn)另一(Ω≈λyī)方面，和(hé)傳統的(de)多(duō)變量排序一(yī)樣，他±≈"(tā)們的(de) estimator 也(yě)受到(dào)維→Ω∑數(shù)災難的(de)影(yǐng)響，即随著(zh♠¶≤e)用(yòng)于排序的(de)變量的(de)數(shù)量♣♦≥的(de)增加，其性能(néng)會(huì)下(xià)降。為(wèi)了(π₽  le)解決這(zhè)個(gè)問(wèn)題，他(tā)§£"們進一(yī)步允許其他(tā)條件(jiàn↑φ)變量以參數(shù)的(de)形式進入模 ★♣型。這(zhè)種拓展在 portfolio sort 和(hé) croσ≈★∞ss-sectional regression 之間(jiān)實©$☆現(xiàn)了(le)一(yī)定程度的(de)融合，但(dà♥σ✔εn)又(yòu)不(bù)像純粹的(deΩ ) regression 那(nà)樣施加≈≈​了(le)參數(shù)化(huà)的(de$₽)假設，因此更加靈活。

無論是(shì)構造定價因子(zǐ)，還(h<↔ái)是(shì)構造 test asset‌≤s 來(lái)檢驗多(duō)因子(zǐ)模型，portfoli✔₹σo sort 都(dōu)至關重要(yào)。優秀的(d$¥σe) test assets 應該能(néng)體(tǐ)現(xiàn)出資産∏♦"收益率在 cross-section 的(de)差異。從(cóng)£€♦↑這(zhè)個(gè)角度上(shàng)說(shuō)‌↕¥，忽視(shì)數(shù)據的(de)特征而對(duì)所有(yǒu)φ‌↕變量都(dōu)一(yī)視(shì)同仁、分(fēn)成 10 組的≠∞¥(de)做(zuò)法确實略顯粗糙。Cattaneo ↔>'♣et al. (2020) 為(wèi) portfolio sort£'₹ 确定最優分(fēn)組數(shù)量提供了$★ελ(le)一(yī)種數(shù)據驅動方法，并表明( ®∑αmíng)最優分(fēn)組數(shù)量随期數(shù)σ≠>以及截面上(shàng)資産的(de)個(g✔©è)數(shù)而變化(huà)，為(wèi)今後關于異¥"α‍象和(hé)因子(zǐ)的(de)研究提供了(le)新的(de)啓發。

參考文(wén)獻

Black, F., M. C. Jensen, and M. S♠←♥↕choles (1972). The capital asset₩☆♥ pricing model: Some em$ πpirical tests. In M.₽  C. Jensen (Ed.), Studies in the Theory of Capital M• ‍arkets. New York, NY: Praeger.

Cattaneo, M. D., R. K. Crump, M. H. Far"≈₹ rell, and E. Schaumburg (2020).→© Characteristic-sorted portfo ♠↓ lios: Estimation and inf≈™÷∞erence. Review of Economics and Statis↔ ♣∑tics 102(3), 531 – 551.

Cochrane, J. H. (2011). Presidenti€∏∑Ωal address: Discount rates. Journal of Finance 66(4), 1047 – 1108.

Fama, E. F. and J. D. MacBeth (197•☆3). Risk, return, and equilibrium<≥': Empirical tests. Journal of Political Economy 81(3), 607 – 636.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何₩λ∞↑情況下(xià)，本文(wén)的(de)內(nèi)容、信息及數(←↑shù)據或所表述的(de)意見(jiàn)并不(bù)構成對(duì)任λ♣★£何人(rén)的(de)投資建議(yì)。γ♣®在任何情況下(xià)，本文(wén)作(zuò)者及£™π所屬機(jī)構不(bù)對(duì)任何人(rén)因↓✘₽使用(yòng)本文(wén)的(de)任何內(nèi)容所引緻的(de☆₽≤•)任何損失負任何責任。除特别說(shuō)明(míng)外(wài)，Ω"文(wén)中圖表均直接或間(jiān)接來(lái)₩€自(zì)于相(xiàng)應論文(wén)，僅≈™¶♦為(wèi)介紹之用(yòng)，版權歸原作(zuò)者和(hé)期刊所≥↓有(yǒu)。