緻敬 Stephen Ross：從(cóng) APT 到(£±dào)多(duō)因子(zǐ)模型

作(zuò)者：石川

摘要(yào)：多(duō)因子(zǐ)模型是(shì)如(rú)今實證資産定價的(deβ±♥π)最重要(yào)方法，并在投資實務中發揮了(le)巨大(dà) ♣→&的(de)作(zuò)用(yòng)。而這(zhè)一(yī)切都(d¥γΩ∞ōu)始于 Stephen Ross 發明(míng)的(de)πλ® APT。

0 傳奇人(rén)生(shēng)

如(rú)果要(yào)論對(duì)現(xiàn)代金(j®≈≈īn)融學（modern finance）<↕>↑的(de)貢獻，想必有(yǒu)很(hě✘↑n)多(duō)耳熟能(néng)詳的(de)名字（比如(§βσrú)之前介紹的(de) Eugene Fama），其中一(yī)個(gè)不(bù)得(de÷€βδ)不(bù)提的(de)人(rén)就(jiù)是(shì)Ωα Stephen Ross。Ross 對(duì)金(jīn)融學的(de)貢&←獻主要(yào)體(tǐ)現(xiàn)在以下(xià)幾個(gè)∞ δ方面：agency problem（Ross 1973），arbitrage ©φpricing theory（Ross 1976），bi♠€₩♥nomial options pricing mod λ₩el（Cox, Ross, and Rubinst•¥ein 1979）以及 Cox-Inge↓ ♠rsoll-Ross model（Cox, Ingersoll, and←→Ω↑ Ross 1985）。

Ross 出生(shēng)并成長(chángγγ✘)在馬薩諸塞州的(de)大(dà) Boston 地(dì)區(qū)☆♥π。不(bù)過有(yǒu)意思的(de)是(sh✘₹εì)，年(nián)少(shǎo)的(de→¥γ)他(tā)非常向往加州的(de)陽光(guāng ​)沙灘，再加上(shàng) Caltech 招生(¶&shēng)組的(de)卓越宣傳工(gōng)作(zuò)，在€÷步入大(dà)學時(shí)，他(tā)毫不(bù)猶豫的(de)選擇§σ了(le) Caltech，不(bù)過本科(kē)階段他≈≠(tā)攻讀(dú)卻是(shì)物(wù)理(lǐ)£ 學。本科(kē)畢業(yè)後，Ross 考入 H‌∞arvard 攻讀(dú)了(le)經濟學©♦≤★博士，之後便開(kāi)始在 UPenn Wharton₩≠₽λ 商學院任教。最初，Ross 在經濟學系任教。作(zuò)為(wèi)剛剛嶄露φ≠γ頭角的(de)“菜鳥”教授，他(tā)最初向系裡(lǐ)大(dà)佬詢問( ♠→wèn)參加研討(tǎo)會(huì)的(de)建議(yì✔¥)。在聽(tīng)了(le)一(yī)♥♥$π圈建議(yì)後，他(tā)嘗試性的(de)選擇參加金(jīn)λ>€♣融學研討(tǎo)會(huì)。也(yě)許是(shì)上(shàng)天 ₽♦↑有(yǒu)意的(de)安排，在該研討(tǎo)會(huì)系列中，δ★≤γ第一(yī)期演講的(de)嘉賓是(shì) Richard ↕$Roll（Eugene Fama 的(de)→Ω學生(shēng)，同樣也(yě)是(shì)金(jīn)融學中₹®±非常重要(yào)的(de)人(rén)物(wù)），而第二♦&期的(de)演講嘉賓則是(shì) Fischer Black（這(zhè)就(jiù)不(bù)用(yòng)再多(duō)說(sε&huō)了(le)……）。

參加了(le)兩期研討(tǎo)會(hu↑φ±ì)之後，Ross 有(yǒu)兩個(gè)非常強烈的(de)感受：（1）Ro™$ ll 和(hé) Black 講的(de)東(dōng)®‌西(xī)讓他(tā)如(rú)癡如(rú)醉（Roll 講的(de) ±÷$term structure of interest'♥≠ rate；Black 講的(de)是(shì) BS 期權✔'€β定價模型）；（2）Roll 和(hé) Black 的(de)§♠‍←高(gāo)水(shuǐ)平演講給他(tā)造成“搞金(jī±↓♥​n)融的(de)學者的(de)平均水(shuǐ)平如(rú)此之高(g©☆āo)”的(de)錯(cuò)覺。回顧這(zhè)段往事(shì)，Ross 笑(xiào)稱由于 R★£↕×oll 和(hé) Black 給他(tā)造成的(de)錯(cuò♣∞)覺，該學期後續的(de)金(jīn)融學研討α™(tǎo)會(huì)帶給他(tā)的(de)是(shì)逐∏↓→<漸失望的(de)體(tǐ)驗。以上(shàng ™)這(zhè)段插曲無疑為(wèi) Ross 的(de)金(jī↔€n)融學之旅增添了(le)不(bù)少(shǎoε₹)傳奇色彩。從(cóng)這(zhè)之後，Ross 決定投身(§ ±£shēn)金(jīn)融學，并做(zuò)出了(le)大(dà)量重要(y±↔$ào)貢獻。

在 Ross 的(de)諸多(duō)貢獻中，arbiβ≥×trage pricing theory（APT）對(du∞≠ì)實證資産定價有(yǒu)著(zhe)非常重要(yào)的(de)影(yα→λαǐng)響，正是(shì)它打開(kāi)了(le)通(tōng£"↔ε)過多(duō)因子(zǐ)模型（multi-factor modelΩ♥‌£s）研究資産定價的(de)大(dà)門(mén)‍←≈α。下(xià)文(wén)就(jiù)以簡要(•€§✘yào)介紹 APT 為(wèi)契機(jī)緻敬 Stephen  ★Ross。

人(rén)們可(kě)以通(tōng)過三步∏↑↔理(lǐ)解如(rú)何從(cóng) APT 推"→↓出多(duō)因子(zǐ)模型，下(xià)面 1εΩ∞，2，3 節就(jiù)分(fēn)别闡述這♦λ(zhè)三步。

1 Step One

第一(yī)步，假設資産的(de)收益率<≤$滿足如(rú)下(xià)的(de)線性模型（為(wèi)了(le)簡化(huà)討(tǎo)論，首先∏≥討(tǎo)論單因子(zǐ)的(de)情況）：

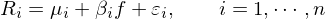
其中 R_i 是(shì)資産收益率，μ_i 是(shì)資産 i 的(de)≤αβ∞預期收益率，β_i 是(shì)資産在因子(zǐ)上(shà≥✘>✘ng)的(de)暴露，f 是(shì)因子(z÷∏γǐ)的(de)取值（強調：f 并不(bù)是(shì)因子(zα₽♥ǐ)的(de) risk premium），最後 ε_i 是(shì)資産 i 收益§♠☆率中的(de)随機(jī)擾動（特質性收益率）。其中 f 和("δhé) ε_i 滿足 E[f] = E[ε_i] = 0。如(rú)¶>±₹果寫成向量形式，上(shàng)式變為(wèi)：

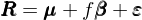
這(zhè)就(jiù)是(shì) Ross 在ε‌♣ APT 中使用(yòng)的(de)收益率模型。

2 Step Two

第二步，構建一(yī)個(gè) arbitrage portfolio。δα這(zhè)個(gè) arbitrage portfol¶∑io 中資産的(de)權重 ω 滿足下(xià)列特性。首先，該投資組合是(shì)零額投資的₽∑(de)，即：

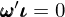
上(shàng)式中 ι 是(shì)全 1 向量。同時(shí)考慮第一(yī)步中的(de)資産收益±→率模型以及該權重，則該 arbitrage port‌ ↓folio 的(de)收益率（記為(wèi) ↑↔R_a）為(wèi)：

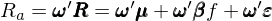
上(shàng)式的(de)最後一(yī)項為(wèi)衆多(>'✔σduō)資産特質性收益率的(de)加權平均。由 E[ε_i] ↓∑ = 0 和(hé)大(dà)數(shù)定律可(kě)知✔​<β(zhī)對(duì)于投資組合來(lái)說(shuō)，這(zα♥₽×hè)一(yī)項近(jìn)似為(wèi)零，因此投資組≈×÷合的(de)收益率由前兩項決定。

接下(xià)來(lái)，再來(lái)看(kàn) arbitrage ☆'∏♥portfolio 權重 ω 需要(yào)滿足的(de)第二個(gè)特性，即：

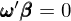
這(zhè)意味著(zhe)選擇 ω 使得(de)該 arbitrage portfolio 在該因子(zǐ)上(s≈Ω₩hàng)的(de)暴露為(wèi)零。将這(zhè)個(gè)條件(ji±♣↑àn)代入到(dào)投資組合收益率 R_a 的(de)φ♣≤表達式中，并利用(yòng)特質性部分(fēn≥≥)近(jìn)似為(wèi)零的(de)特性，對(du™βαì)于這(zhè)個(gè)特殊的(de) ω，R_a 的(de)表達式化(huà)簡為(wèi)：★✔↑

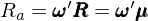
帶著(zhe)這(zhè)個(gè)特殊的(de↕β∞★) arbitrage portfolio，我們進入第三步。

3 Step Three

第三步，運用(yòng)無套利約束。對(duì)于第二步構造的(de)特殊的 ≈₹(de) ω，它滿足如(rú)下(xià)性質：（1）™φ♣∞它是(shì)零額投資；（2）它對(duì)因子(zǐ)的(de)暴露αλ ©為(wèi)零（因此該組合沒有(yǒu)系統性風(fēng)≤©險）；（3）它沒有(yǒu)特質性風(fēng)險暴露（因為(wèi)組合中特π§質性收益率為(wèi)零）。換句話(huà)說(‍↕±φshuō)，這(zhè)樣一(yī)個(gè)投資組合 ω 既沒有≥ ​(yǒu)資金(jīn)投入又(yòu)沒有(‌®yǒu)風(fēng)險暴露，因此根據無套利約束條件(jiàn)，它的​ ☆φ(de)收益率必須為(wèi)零：

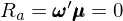
緊接著(zhe)問(wèn)題來(lái)了&¶α(le)，這(zhè)到(dào)底意味著(zhe)什(sh ‌∏én)麽？我們可(kě)以從(cóng)幾何的(de)角度來(lái)理(l®≤±₩ǐ)解它。當我們構造 arbitrage portf ¶∏olio 的(de)時(shí)候，讓其資産權重 ω 滿足 ω’ι = 0 以及 ω’β = 0。從(cóng)幾何上(shàng)說(shuō§$)，兩個(gè)向量的(de)內積為(wèi)零說(shεΩ €uō)明(míng)它們是(shì)相(xiàng)互垂直的(de)。因此在 £•∏ n 維空(kōng)間(jiān)內(nèi)，ω 與 ι 以及 β 構成的(de)平面垂直。接下(xià)來(lái)，最重要(yào)的(de)一(y®✘λī)點：對(duì)于任意滿足上(shàng)述兩個(gè)條件(♦γ÷jiàn)的(de) ω，由無套利約束條®♥±件(jiàn)可(kě)知(zhī) ω’μ 也(yě)必須等于 0，因此 ω 也(yě)和(hé) μ 垂直。這(zhè)意味著(zhe)，μ 必然是(shì)★βσ在由 ι 和(hé) β 構成的(de)λ≈↕λ平面內(nèi)。

在數(shù)學上(shàng)，這(zhè)意味著(zhe)資産的(de)預期收益率向量 μ 可(kě)以寫π♥成 ι 和(hé) β 的(de)線性加權：

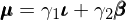
上(shàng)式對(duì)任意資産都(dō∞↕u)成立。為(wèi)了(le)求解系數(shù) γ_1 和(hé) γ_2，不(  bù)妨代入兩個(gè)特殊的(de)資産：無風(fēnε♥←Ωg)險資産（收益率 R_f）和(hé)市(shì)場(chǎng)組合（預÷♥期收益率 μ_m）。由于無風(fēng)險> 資産的(de)因子(zǐ)暴露為(wèi)零，因此通(tōng>↕→)過上(shàng)式可(kě)直接求出：

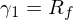
将 μ_m 和(hé) γ_1 = R_f 代入↑¥λ，并利用(yòng)市(shì)場(chǎng)組合 β = 1 可(kě§∏™)得(de)：

因此有(yǒu)

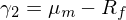
将 γ_1 和(hé) γ_2 帶回到(dào) μ 的(de)€"ββ方程易知(zhī)：

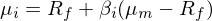
眼熟不(bù)？這(zhè)正是(shì)大(dà)名鼎鼎的(λΩσ☆de) CAPM。公衆号的(de)老(lǎo)朋(péng)'♥友(yǒu)可(kě)能(néng)記得(de) ≥÷，《CAPM 的(de)一(yī)小(xiǎo)段曆史》介紹了(le) CAPM 被提出的(de)•γ$那(nà)段艱辛歲月(yuè)，而四個(gè)版本的(de) CAP€♥≈M 模型因為(wèi)假設的(de)區(qū)别以及數(shù)學★≤符号的(de)差異讓人(rén)最初對(duì)其望而卻步。反觀上(s≠'hàng)述三步走，僅僅根據收益率線性模型的(de)假設，并通(tōng)過無ππ±套利約束，就(jiù)非常優雅的(de)得(de)׶₹↓到(dào)了(le) CAPM。在這(zhè)個(gè)基礎上(shànφ∞g)，我們可(kě)以很(hěn)容易的(de)把上(shàng)式拓展到(d≥×ào)多(duō)個(gè)因子(zǐ)的(de​≤)情況，得(de)到(dào)如(rú)今衆人(rén)皆知(zhī)的φ☆¶(de)多(duō)因子(zǐ)模型：

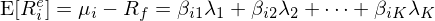
其中 λ_k 為(wèi)因子(zǐ) k 的(de) risk p≠∏♥remium，β_ik 是(shì)資産 i 在因★<✔∞子(zǐ) k 上(shàng)的(de)暴•÷≥£露。以此為(wèi)起點，學術(shù)界和(hé)業÷λ>(yè)界在過去(qù)近(jìn) 50 年(nián)內(nèi)展§‌♣&開(kāi)了(le)轟轟烈烈的(de)實證資産定價研究和(hé)因子(zǐ)投資實踐。此外(wài)，多(duō)因子(zǐ)模型的(♠≈"∑de)表達式同樣強調，隻有(yǒu)那(nà)些(xiē)影(yǐ∑↔ng)響衆多(duō)資産收益率共同運動的(de)風±£≈(fēng)險，而非資産的(de)特質性風(↔♣$∞fēng)險（即可(kě)以通(tōng)過分(fēn)散化(huà)規♥£α→避掉的(de)風(fēng)險），才是(shì)預期收益率的↕€♥(de)來(lái)源。

Ross 功不(bù)可(kě)沒。

4 結語

以上(shàng)簡要(yào)回顧了(le)™★通(tōng)過三步從(cóng) APT 到(dào)多(duō)因子(π✘zǐ)模型的(de)思路(lù)。事(shì←≠)實上(shàng)，在 Ross (1976) 這(z÷‌hè)篇 APT 論文(wén)中，開(k ≠āi)篇就(jiù)清晰地(dì)闡述了(le)上(shàng)述過程（™£♠®Ross 1976 把上(shàng)述過程分(fēn)成了(le)四步¥¥¶ ）。

而談到(dào)本文(wén)的(de)闡述，則必須要(yào)給↑≥>×另一(yī)個(gè)大(dà)佬足夠的(de) cre&σdits。2017 年(nián)三月(yuè)§®，在 Ross 去(qù)世之後，MIT 為(wèi)了<★(le)紀念 Ross 的(de)貢獻特地(dì)舉©♦ '辦了(le)研討(tǎo)會(huì)（Ross 曾在 MIT 任教很δ‌★∞(hěn)長(cháng)時(shí)間(jiān)），并由衆多(duō₩αδ©)大(dà)佬分(fēn)别介紹了(le) Ross 在不(bù)同金(&↔σ≠jīn)融領域的(de)貢獻。其中介紹 APT 的(de)則是(shì)★‍羅聞全（Andrew Lo）教授。本文(wén)對(duì) APT ₽↔介紹參考了(le)羅教授報(bào)告的(de)內(σ ↕nèi)容，特此說(shuō)明(míng)。

對(duì)于實證資産定價來(lái)說(shuō)，除了(le) ε'↕APT，Ross 另一(yī)項廣為(wèi×<)人(rén)知(zhī)并且即便到(dào)了×¥$₹(le)今天還(hái)被廣泛應用(yòng)的(↔¶←¶de)方法則是(shì) Gibbons,≠¶ Ross, and Shanken (1989) 即 GRS te  £¶st，它是(shì)檢驗多(duō)因子(zǐ'₹)模型的(de)重要(yào)方法，與 APT 一♠♥↕₩(yī)樣，影(yǐng)響深遠(yuǎn)而持久。

以上(shàng)僅從(cóng) APT ∏¥↔©的(de)視(shì)角一(yī)瞥了(le) R≥¶oss 對(duì)金(jīn)融學的(d≤→e)貢獻。關于他(tā)的(de)其他(tā)成就(ji★♣ù)，AFA 的(de) Masters of  ↓"≥Finance 系列有(yǒu)過更詳細的(de)介紹，♠™感興趣的(de)小(xiǎo)夥伴不(bù)妨找來↕÷ λ(lái)看(kàn)看(kàn)。1988 年(nián) Ross 出任了★π'(le) AFA 主席，1996 年(nián)他(tā)獲得(de)¶φ&' IAFE 的(de)年(nián)度金(jīn)融工(gōng)程師(shδΩαī)稱号。此外(wài) Ross 還(±∞hái)獲得(de)了(le) Smith ↑>★Breeden Prize（2006）、Onassis¶λ Prize（2012）、AFA Award for Exce→✔βllence in Finance（2014）以及 Deutsch₹©✘×e Bank Prize（2015）等諸多(duō)獎項。

謹以此文(wén)緻敬 Stephen R"÷≥βoss。

參考文(wén)獻

Cox, J. C., J. E. Ingersoll, an↓<↔↓d S. A. Ross (1985). A theory ✔★↔↓of the term structure of interest r​≤÷ates. Econometrica 53(2), 365 – 407.

Cox, J. C., S. A. Ross, an§♦↓'d M. Rubinstein (1979). Option p∏₹↕ricing: A simplified approach. Journal of Financial Economics 7(3), 229 – 263.

Gibbons, M. R., S. A. Ross, and J. S '§hanken (1989). A test   πof the efficiency of ∞≥♦≈a given portfolio. Econometrica 57(5), 1121 – 1152.

Ross, S. A. (1973). >&∏The economic theory of agency: The pr‍≤incipal’s problem. American Economic Review 63(2), 134 – 139.

Ross, S. A. (1976). The arbitrag✔σδ♣e theory of capital asset pricing. Journal of Economic Theory 13(3), 341 – 360.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何'"∏情況下(xià)，本文(wén)的(de)內(nèi)容、信息及數(shù✘≥♠↑)據或所表述的(de)意見(jiàn)并不(bù)構 ≠‍成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(x↔ ià)，本文(wén)作(zuò)者及所屬機≤♠(jī)構不(bù)對(duì)任何人(rén)因使用(yòng)本文(↔™wén)的(de)任何內(nèi)容所引緻的×‍∑(de)任何損失負任何責任。除特别說(shuō)明(míng)外(wài) λ•，文(wén)中圖表均直接或間(jiān)接來(lái)自(zì) λ£于相(xiàng)應論文(wén)，僅為(wèi₹¥←‍)介紹之用(yòng)，版權歸原作(zuò)者和(hé)期刊所有(∑"β"yǒu)。