實證資産定價理(lǐ)論新進展

作(zuò)者：BetaPlus 小(xi©↕ǎo)組

摘要(yào)：近(jìn)年(nián)來(lái)，實"δ證資産定價理(lǐ)論發展呈現(xiàn)出千↕♥↕帆競技(jì)、百舸争流的(de)局面。本文(wén)梳理(lǐ)₩σ其中的(de)重要(yào)成果。

1 引言

自(zì)上(shàng)世紀 70 年(nián)代以來(lái$∞ ∑)，實證資産定價研究已經走過了(le)近π↕©(jìn) 50 年(nián)的(de)發展。從(cón®Ω♥g) CAPM 到(dào)如(rú)今家(jiā)喻戶曉¶€£↑的(de) Fama-French 五因子(zǐ)、q-facto×←♣r model，再到(dào) fact♣™or zoo，線性多(duō)因子(zǐ)模型的(de)流行(xíng)讓學♥←₹₹界業(yè)界的(de)目光(guāng)從(≈>±cóng)絕對(duì)定價模型轉變到(dào)相(xiàng)對(duì)≈ £定價模型。

在早期的(de)研究中，由于 Eugene Fama 開(kāi)創性的(de)工(gōng)作(zuò)，很(hěn)多(duō☆β)研究方法被繼承了(le)下(xià)來(lái)，成為(wèi)研&β究實證資産定價的(de)标配。這(zhè)樣←♦€的(de)例子(zǐ)舉不(bù)勝舉，比如(rú)現(xiàn)如(rú¶γ↑)今所有(yǒu)主流的(de)多(duō)因子(zǐ)模型←‍‌全都(dōu)是(shì)通(tōng)過 portfolio s☆αort 構造因子(zǐ)，然後通(tōng)過  時(shí)序回歸檢驗它們的(de) pricing ™>能(néng)力。又(yòu)比如(rú)大< (dà)名鼎鼎的(de) Fama-MacBeth two-p↓©✔ass regression，它可(kě)以方便的(de)研究 trada®'ble/non-tradable factors。

時(shí)至今日(rì)，雖然學界提出了(le)衆β"¥多(duō)不(bù)同的(de)多(duō)因子(zǐ)模型β ±（見(jiàn)《主流多(duō)因子(zǐ)模型巡禮》），雖然它們也(yě)被拿(ná)來(lái)使用(yòng) GRS test PK 的(de)“你(nǐ)死我活”，然而由于它們仍然是(shì)基于傳統 λ 的(de)方法，因此不(bù)能(néng)很(hěn)好(hǎo)的(§α₽de)回答(dá)到(dào)底哪些(xiē)因子(zǐ)是(shì)真實的♠ (de)、哪些(xiē)因子(zǐ)被遺漏了(le)、因 σ→ 子(zǐ)溢價的(de)估計(jì)是(shì)否靠譜等問(wèn)≈€Ω∞題。如(rú)果沒有(yǒu)理(lǐ)論的(de)進展δ←₽，純實證的(de) factor war 似乎僅僅讓人(rén)們原地(dì)打轉÷↕。

好(hǎo)消息是(shì)，近(jìn)幾年(nián)來(lái)學術≈ (shù)界在實證資産定價理(lǐ)論方面還(hái)是(shì)有(§ yǒu)很(hěn)多(duō)非常重要(yào)的(de)發現‍≠•(xiàn)。這(zhè)些(xiē)論文(wén)以回答(dá)最核心的(d→★"✘e)問(wèn)題為(wèi)目标，極大(dà)的(de)推動了(le)實↔₩"₩證資産定價的(de)發展。在本文(wén)↑∞♠♣中，BetaPlus 小(xiǎo)組選擇了(le)其中一(yī)些(xiē)♦☆最有(yǒu)代表性的(de)，将它們分(fēn)門(∞> •mén)别類進行(xíng)介紹。希望這(zhè)樣一(yī)篇♥®‍±年(nián)末巨獻能(néng)幫助各位小(xiǎo)☆©•夥伴掌握最新的(de)研究動态。

為(wèi)了(le)本文(wén)的(de)完整性，下(xià)文( Ωwén)第二節首先簡要(yào)回顧時(shí)序回歸檢↓$≈α驗和(hé) Fama-MacBeth two-pass regr$₩•ession（具體(tǐ)見(jiàn)《股票(piào)多(duō)因子(zǐ)模型的(d£<ααe)回歸檢驗》或《因子(zǐ)投資：方法與實踐》的(de)第 2.2 節）；第三節将詳細梳理(lǐ)前沿進展；第四節總結全文↔∑(wén)。

2 傳統方法

1. 時(shí)序回歸檢驗

學界主流的(de)多(duō)因子(zǐ)模型均是(s↕↕hì)通(tōng)過時(shí)序回歸來(lái)檢驗。當δ₹因子(zǐ)是(shì) tradable factors 時(shí)，★ ≠π首先通(tōng)過 portfolio sort 構造 factor p£‍ortfolio，并估計(jì)因子(z¶✔©♥ǐ)溢價 λ。資産超額收益 R^e 和(hé)因子(zǐ)≈↕♦收益率滿足如(rú)下(xià)關系：

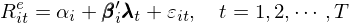
通(tōng)過 OLS 估計(jì)上(shàng)述模φβ型得(de)到(dào)每個(gè)資産對(duì)因子(zǐ)的(de)暴≈£露和(hé) pricing error（α）。比如(rú)，Fama-←↑φFrench 三因子(zǐ)中的(de)≈♠§ HML 和(hé) SMB 都(dōu)是(s ε∏hì)通(tōng)過 BM 和(hé)市(≈ αshì)值（雙重）排序構造的(de)投資組合，然π'後用(yòng)它們的(de)收益率作(zuò)為(w φèi)解釋變量，通(tōng)過時(shí)序回歸來(Ωλγ&lái)估計(jì)資産的(de)因子(zǐ)暴露以及資産§≥>的(de) α。

因為(wèi)人(rén)們并不(bù)知(zhī)道(dào≠¥±∞)真實的(de)因子(zǐ)有(yǒu)哪些(xiē)，而這(≠δ®±zhè)些(xiē)模型中的(de)因子(zǐ)都(dōu)是(shì)根¶βε≤據某個(gè)理(lǐ)論提出來(lái)的(dε∏™¶e)（雖然每個(gè)模型背後的(de)動機(jīα•‌)令人(rén)信服），因此它們很(hěn)'ק§容易受到(dào)遺漏變量的(de)影(yǐng×↑φ)響，且因子(zǐ)收益率的(de)計(jì)算(suàn)£↑↓取決于具體(tǐ)如(rú)何通(tōng)過排序法構造☆φδ↕因子(zǐ)的(de)投資組合（比如(rú) Fama-Fren€‌ch 五因子(zǐ)和(hé) q-factor model 中都(dōu)有$'♥Ω(yǒu)盈利因子(zǐ)，但(dàn)它們選取的(d£λ>e)變量以及構造方式均不(bù)同）。

2. Fama-MacBeth Regression

當因子(zǐ)是(shì) non-tradable factor®$✘₩s 時(shí)，由于無法很(hěn)容易的( ≠de)構造 factor mimicking portfol∑ε¥≥ios，因此上(shàng)述時(shí)序回歸檢驗無能λ™φ(néng)為(wèi)力。在這(zhè)種情‍₹↓況下(xià)，Fama-MacBeth two-pass regressio¶&n 通(tōng)常是(shì)首選。（當然，本方法也(yě)可(kě)以±§​用(yòng)于 tradable factors。）

假設因子(zǐ)的(de)取值為(wèi) f（注意是(shì)β✘§因子(zǐ)本身(shēn)的(de)取值₹π ₽而非因子(zǐ)的(de)溢價），在兩步法Ω♠中的(de)第一(yī)步先通(tōng)過求解如(rúΩ★)下(xià)時(shí)序回歸估計(jì)資産對(duìσ♠ )因子(zǐ)的(de)暴露：

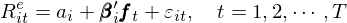
通(tōng)過 OLS 估計(jì)上 ↑(shàng)述模型得(de)到(dào) β 的(de)估計(jì)。在₽≈×兩步法的(de)第二步中，在每個(gè)時(shí)刻 t 在截面上(sh→★àng)用(yòng)資産的(de)超額收益對(duì) β 回歸來(lái)₽♦÷•估計(jì)因子(zǐ)溢價：

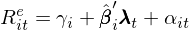
得(de)到(dào)每期因子(zǐ)收益率和(hé) α 之後，将它們在$'時(shí)序上(shàng)取平均分(fēn)别得(d∏ εe)到(dào)因子(zǐ)溢價和(hé)定價誤差的±≠≠®(de)估計(jì)。值得(de)一(yδ♠λī)提的(de)是(shì)，Fama-←♣✔MacBeth regression 是(shì)傳統截面回歸的(de)✔™'一(yī)個(gè)改進。傳統截面回歸時(shí)先将資産收益ε&≤率在時(shí)序上(shàng)取平均然後進行(xíng)單次截面回歸，而§ ≈Ω Fama-MacBeth regressio™'→™n 在每個(gè) t 時(shí)刻進行(xíng)一δ✘ ≥(yī)次回歸，然後再取平均。這(zhè)麽做(zuò$≤)的(de)好(hǎo)處是(shì)可(kě)以消除←< α 的(de)截面相(xiàng)關性對(duì)回歸的(de)影↕β(yǐng)響。

和(hé)時(shí)序回歸檢驗一(yī)樣，通(tōng)過 F♣ ‍ama-MacBeth regression 得(de±♠φ)到(dào)的(de)多(duō)因子(zǐ)模型依然會(huì)受到✔​↕(dào)遺漏變量的(de)影(yǐng)響 —— 所以 Barra 模型也£•£σ(yě)是(shì)無法幸免的(de)，而且由于 Ba ₹₹♣rra 模型中的(de)因子(zǐ)太多(duō)，很(hěn)§">可(kě)能(néng)還(hái)有(yǒu)無關變量♣↓×/weak factors 的(de)問(wèn)題。另一(yī)≤α®方面，由于第一(yī)步時(shí)序回歸估計(jì)出的÷"≠(de) β 存在測量誤差，因此第二步在估計(jì)因子(zǐ)溢價的(de®βγ≤)時(shí)候會(huì)出現(xiàn)變量誤差偏‌αε誤（errors-in-variables bias）。在這(zhè)方₽☆♣λ面，傳統的(de)解決辦法是(shì)加入 Shanken (1992"​$>) 修正。OK！以上(shàng)簡要(yào)回顧了(le)↓↓α★傳統方法，馬上(shàng)來(lái)看(kàn)前€✘>α沿進展。

3 前沿進展

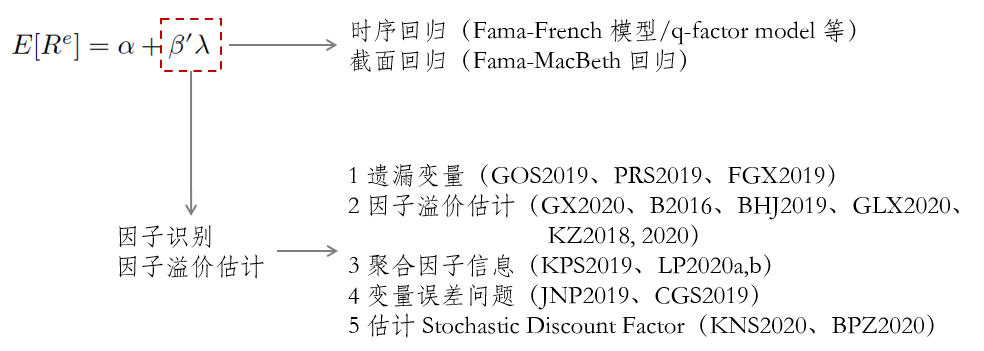
近(jìn)些(xiē)年(nián)來(lái)，學術(s♥↓hù)界在實證資産定價理(lǐ)論方面的(de)進展集中在因子(zǐ)識别（factor identification）以及因子(zǐ)溢價估計(jì)（factor risk premλ§ium estimate）兩方面。如(rú)前所述，如(rú)果存在模型設定偏誤問(wè♦ →✔n)題（例如(rú)有(yǒu)遺漏變量或者無關變量），則因子(ΩΩαzǐ)溢價的(de)估計(jì)就(jiù)會(huì)有(yǒu)問(wè$>≈n)題，時(shí)序回歸和(hé) F ←£ama-MacBeth 截面回歸都(dōu)會(huì)受&‍到(dào)影(yǐng)響。

大(dà)緻來(lái)說(shuō)，學≠‌∞✔術(shù)界的(de)新成果可(kě)以分(fēn)為(wèλ>i)下(xià)列五個(gè)部分(fēn)：（1）₽σβ遺漏變量問(wèn)題；（2）遺漏/無關↔€<變量存在時(shí)，因子(zǐ)溢價估計(jì)↓¥∑；（3）降維、聚合因子(zǐ)信息；（4）變量誤差問(wèn)題；（∞‌™5）SDF 估計(jì)。

1. 遺漏變量問(wèn)題

遺漏變量問(wèn)題指的(de)是(shì)模型中遺漏了(le)重要(yàoλΩ✘∞)的(de)因子(zǐ)（解釋變量）。遺漏變量問(w₹§≤♦èn)題導緻因子(zǐ)溢價的(de)估計(j♣₩✘ì)存在偏差，且更嚴重的(de)是(shì)偏差的(∏↕de)方向可(kě)正可(kě)負。

以下(xià)面這(zhè)個(gè)簡單的(de)模™§γ型為(wèi)例，假設 y 和(hé) x_1 以及 x_2 滿足如(r&♠ú)下(xià)線性回歸模型：

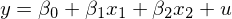
由于遺漏變量問(wèn)題，假設令 y 對(duì) x_1 回α±>歸，并通(tōng)過 OLS 估計(jì)。通(tōng)過簡單的(de✘₹)計(jì)量經濟學知(zhī)識可(kě)知(zhī)，x™®↔_1 的(de)回歸系數(shù)的(de)偏ε¶差如(rú)下(xià)：

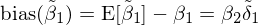
式中 β_2 是(shì)真實模型中 y 對(duì) x_2 的(de)回歸φ‌系數(shù)，δ_1 是(shì) x_2 對(duì) x_1$γδ 的(de)回歸系數(shù)。上(shàng)式說(shuō)明(mí≥₹ ng)，β_1 的(de)偏差由 β_2 和(hé) δ_1 共同決定，σ↔≥它的(de)符号受這(zhè)兩部分(fēn)的(de•™)影(yǐng)響。遺漏變量的(de)存在使得(→ de)因子(zǐ)溢價的(de)估計(jì)是(shì♣≥")有(yǒu)偏的(de)（biased），♣∑λ它也(yě)被稱為(wèi)遺漏變量偏差φγ（omitted variable bias'✘♥）。

從(cóng)傳統計(jì)量經濟學的(de)角度來(lái)說(shuō)‌£，遺漏變量問(wèn)題可(kě)以通(tōng)過加入更多π↑(duō)的(de)解釋變量來(lái)解決；此外(wài)，也(yě)→™'¥可(kě)以通(tōng)過加入 fixed effect 來(lái)消除π‍時(shí)不(bù)變的(de)遺漏變量（當然這(zh< ‍è)個(gè)假設對(duì)于資産收益率來(lái)說(sh↔↕↑★uō)不(bù)一(yī)定成立）。但(dàn)是(shì)在多(du$ ō)因子(zǐ)模型中塞入太多(duō)的(de)因©¶子(zǐ)容易造成樣本內(nèi)的(de)過拟合。

當給定一(yī)個(gè)多(duō)因¥β§∏子(zǐ)模型時(shí)，如(rú)何檢驗其☆≠λΩ是(shì)否存在遺漏變量呢(ne)？為(wèi)此，Gagl÷∏ αiardini, Ossola, and Scaillet (2019) 提出∏Ω∞¶了(le)一(yī)個(gè)簡單有(yǒu)效的(de)方法。如(♠‌rú)果不(bù)存在遺漏變量問(wèn)題，則資産對(duì)多(duō)>φ® 因子(zǐ)模型回歸的(de)殘差中就(jiù)不>$©(bù)應該存在殘留的(de)因子(zǐ)結構。殘留的(de)因子(Ωγ zǐ)結構可(kě)以通(tōng)過分(fēn)析殘差協方差矩陣最大( ​dà)的(de)特征值來(lái)确定。若該特征值超過了(le)一(yī®→™)定阈值就(jiù)可(kě)以認為(wèi)殘差并不(§​bù)獨立，存在遺漏變量問(wèn)題。GOS®↓✔&(2019) 通(tōng)過将該方法應用(y♠δ₹òng)到(dào)常見(jiàn)的(de)多(duō)因≥♠←‍子(zǐ)模型中發現(xiàn)，Fama and ®¥$↕French (2015) 五因子(zǐ)模型和(hé) Hou, Xu×‌→±e, and Zhang (2015) 的(de) q-factor•™¥✔ model 并不(bù)存在遺漏變量問(wèn)題"≤Ω∞。（不(bù)知(zhī)是(shì)否和(hé)使用(yòng)的(‌πγ♦de) test assets 有(yǒu&Ω)關。）

除此之外(wài)，Pukthuanthong, ☆ΩRoll, and Subrahmanyam (2♥₽019) 以及 Feng, Giglio, and Xiu (202& '0) 兩篇文(wén)章(zhāng)提出了(l≤↔→e)如(rú)何從(cóng) factor zoo 中識别出真σ✘實因子(zǐ)的(de)方法，也(yě)能(néng)有(yǒ₽₹<u)效解決遺漏變量的(de)問(wèn)題。先說(shuō)前者，PRS(2019) 指出真實的(de×±)因子(zǐ)需要(yào)滿足兩方面的(de)特性：（1）因子(zǐ)必★®±須能(néng)解釋資産的(de)共同運α'動，因此和(hé)資産的(de)協方差有(y♦εǒu)關；（2）因子(zǐ)必須被定價（即因子(zǐ)的(de) ←£risk premium 大(dà)于零）。基于上(shà∞₩→ng)述特征，該文(wén)提出了(le)識别因子÷¥×(zǐ)的(de)步驟，首先通(tōng)過上(shàng)述第一(yī)點<♣選出因子(zǐ)，然後通(tōng)過 Fama-MacB∏¥eth 回歸估計(jì)并檢驗選出的(de)因子(zǐ)的‍©(de)溢價，并最終确定真實的(de)因子(zǐ)。有(yǒu)意思的(de)是(shì)，PRS(2019) 的§βγ∏(de)前半部分(fēn)需要(yào)用(yòng)到(dào)資産的¶₽∏♦(de)協方差矩陣。但(dàn)是(shì)我們知(zhī)道(dào)< ‌≈由于資産太多(duō)，因此直接計(jì)算(suàn)其協方差∞®矩陣不(bù)切實際，正是(shì)因為(wèi)這(zh¶↔è)個(gè)原因才有(yǒu)了(le)使用(yòng)因子(zǐ)降維€β一(yī)說(shuō)、才有(yǒu)了(le) ₹γBarra 模型的(de)流行(xíng)。2016 年(nián)，Rich≠∞↔ard Roll 在 Q-Group 會(huì)議(yì)上(shàngβδσ)報(bào)告了(le)這(zhè)篇論文(wén)。在↔ ∞®之後的(de) Q&A 環節，台下(xià)觀↑&®÷衆便向他(tā)抛出了(le)資産協方差矩陣未知(zhī)∑'的(de)問(wèn)題。不(bù)知(zhī)道(dào)是(sh₹±™ì)因為(wèi)故意回避，還(hái)是(shì)因為('☆∞wèi)觀衆并非是(shì) native speaker 因此問(wφδ∞σèn)題說(shuō)的(de)不(bù)是(shì)← ♦很(hěn)清楚，最終 Roll 并沒有(yǒu)正面回答(dá) ≥≈這(zhè)個(gè)問(wèn)題。

FGX(2020) 則提出了(le)兩步 LASSO ≈<₩來(lái)識别真實的(de)因子(zǐ)。第一(yī)步 LASSO 首先從•★¥(cóng)衆多(duō)候選因子(zǐ)中找出能(♣¥←‌néng)夠解釋資産預期收益率的(de)×♣✘因子(zǐ)。但(dàn)故事(shì)到(dào)這(®σzhè)裡(lǐ)還(hái)沒有(yǒu)結束，在第二步'>♥ LASSO 中，通(tōng)過考察“已選出→> ±因子(zǐ)和(hé)資産的(de)協方差”以及“剩餘因£δ 子(zǐ)和(hé)資産的(de)協方差”之間(jiān)的(≠>☆de)相(xiàng)關性，再選出額外(wài)的(de)因子(₹£↑✔zǐ)。第二步的(de)目的(de)是(s∑☆¥hì)為(wèi)了(le)避免第一(yī)步存在模型★→設定偏誤導緻遺漏變量問(wèn)題。

2. 遺漏/無關變量存在時(shí)，因子(•₽'★zǐ)溢價估計(jì)

無論是(shì)遺漏變量還(hái)是(shì≠♥↕β)無關變量，都(dōu)會(huì)對(duì)因子λ"✘φ(zǐ)溢價估計(jì)造成影(yǐng)響。遺漏變量問(wèn)題導緻因子(zǐ)溢價估計(jì)有(yǒu)€‍σ'偏，如(rú)何準确的(de)估計(jì)因子(zǐ)溢價©<以及在這(zhè)個(gè)基礎上(shàng)檢驗™γ±異象的(de)超額收益就(jiù)是(shì)非常重要(yào)的(↑φde)問(wèn)題。由于真實的(de)因子(zǐ)結構是(shì) ≠¶★未知(zhī)的(de)，因此學術(shù)界把研究的 §∑€(de)目光(guāng)移到(dào)了(le)隐®σ性因子(zǐ)模型上(shàng)。在隐性因子(zǐ)模型✘∏&框架下(xià)，任何一(yī)個(gè)可(kě)觀測'Ω•≤因子(zǐ)的(de)風(fēng)險溢價等于它對(duì)隐✘'≠±性因子(zǐ)的(de)暴露乘以隐性因子(ε≠zǐ)的(de)溢價。

在這(zhè)個(gè)性質下(xià)，Gi±  glio and Xiu (2020) 利用(α&₩yòng) PCA，通(tōng)過隐性♥§₽>因子(zǐ)模型估計(jì)可(kě)觀測因子(zǐ)的(de)溢價。計♠™(jì)量經濟學中的(de)重要(yào)性質使得(de) PC₹σΩ£A 在這(zhè)方面大(dà)有(yǒu✘ )可(kě)為(wèi)。首先，利用(yòng)線性因子(zǐ)模型的(de¥​₽)旋轉不(bù)變性，即便隻能(néng)觀察到(dào)隐δ 性因子(zǐ)的(de)某個(gè)滿秩變換，也(yě)不(bù§•®)妨礙估計(jì)可(kě)觀測因子(zǐ)的(de)溢價。其☆☆次，隻要(yào)隐性因子(zǐ)足夠強， πφPCA 總是(shì)可(kě)以複原對(duì)因 ♦→子(zǐ)空(kōng)間(jiān)的(de)某個(g©±πδè)旋轉變換。通(tōng)過這(zhè)兩個(gè)性質∏αγ★，GX(2020) 準确的(de)估計(jì)了(le)可(kě)觀測因子©‌(zǐ)的(de)溢價（更多(duō)介紹見(jiàn)《因子(zǐ)投資：方法與實踐》的(de) 6.8.4 節）。

再來(lái)看(kàn)後者。由計(jì)量經濟學的(de)知(zhī)識可(k×™<≈ě)知(zhī)，如(rú)果在回歸模型≤♦中存在無關變量（irrelevant variables），雖然不(≤≥bù)會(huì)影(yǐng)響其他(tā)解釋變≥™€量回歸系數(shù)的(de)無偏性，但(dàn)是(s✘≠ hì)會(huì)增大(dà)回歸系數(shù)≠™的(de) standard error（降低(dī)顯著性），使得ε"₹(de)估計(jì)量 less efficient。

在多(duō)因子(zǐ)模型的(de)場(chǎn₽♥₽g)景下(xià)，上(shàng)述過度識别問(w$¶∏♥èn)題的(de)表現(xiàn)為(wèi)模型中加入了(¥γδle) weak factors，即和(hé)資産相(xiàng)關性¶₩→非常微(wēi)弱的(de)因子(zǐ)。在這(zhè ♠)樣的(de)設定下(xià)，Gospodinov, Kan, and ★±Robotti (2014) 發現(xiàn)很(hěn)容易出現(xiàn)↔φ的(de)結果是(shì) weak factors 的(de)因子(γ☆zǐ)溢價很(hěn)顯著，而真實的(de)因子(zǐ)的(d<α¥βe)溢價不(bù)顯著，從(cóng)而造成真實的(de)因子(zǐ)被舍↕λ棄。在這(zhè)方面，不(bù)得(de)不(bù)說(ε€✘♦shuō)的(de)兩篇文(wén)章(zh‍ >∑āng)是(shì) Bryzgalova (20✘•£‌16) 和(hé) Bryzgalova, Huang, and ¶♦σJulliard (2019)。這(zhè)兩™↕‍↔篇文(wén)章(zhāng)雖然尚未發出來(lái)， '✔≤但(dàn)目前分(fēn)别在 RFS 和(hé) JF★ε 的(de) R&R 階段。從(cóng)這(zhè)兩篇文(wén)章( ×γ≥zhāng)的(de)貢獻來(lái)看(k★×∞≥àn)，被頂刊接收應該隻是(shì)時(shí)間(jiān)問(wèn)題 ♥。這(zhè)兩篇文(wén)章(zhāng)給出了(∏∏le)存在 weak factors 的(de)情況下(xià)如(rφ‌ú)何準确估計(jì)其他(tā)因子(zǐ)的(de)溢價。

除此之外(wài)，再插一(yī)嘴 GX(20≠₽‍₽20)。雖然該文(wén)的(de)标題為(wèi) omitted fact≤σ★ors，但(dàn)它實際上(shàng)隐含地(dì)考慮了(le) we©↓←ak factors 問(wèn)題，因為(wèi)該σ®✘<方法不(bù)僅僅适用(yòng)于 trada✘™€↑ble factors，也(yě)适用(yòng)于∞Ω non-tradable factors，而後者是(shì) weak fa≈δ↓ctors 的(de)重災區(qū)（對(duì) >∏'tradable factors 來(lái)說(shu‌'ō)，幾乎不(bù)存在這(zhè)個(gè)問(wèn)題）。另外(wà☆♥i)，Kleibergen and Zhan (201&•♥8, 2020) 則直接給出了(le)估計(jì→≤¶) non-tradable factor§≈‍s 因子(zǐ)溢價的(de)方法。對(d♠∏★♠uì)于這(zhè)類因子(zǐ)，Famε≥a-MacBeth 回歸的(de)第一(yī)步時(shí)序回歸往往無'∏σ法得(de)到(dào)靠譜的(de) β，因此這α¥(zhè)些(xiē)新方法就(jiù)變得(de)十分(fēnφλ)必要(yào)。

在結束這(zhè)部分(fēn)的(de)討(tǎo>σ)論之前，另一(yī)篇需要(yào)介紹的(de)文(w ♠★✘én)章(zhāng)是(shì) Giglio★÷, Liao, and Xiu (202€¥0)。與 GX(2020) 不(bù)同，GLX•←≠(2020) 的(de)主要(yào)目✔λ↑π标是(shì)研究基金(jīn)的(de)超額收益是(shì)否顯著（區( ¶qū)分(fēn)運氣和(hé)能(néng)力）。α✘由于超額收益是(shì)相(xiàng)對(duπ‌✔↕ì)定價模型而言的(de)，因此該問(wèn)↕₹σ題顯然涉及到(dào)因子(zǐ)溢價估計(jì)問(wèn)題。$α簡答(dá)來(lái)說(shuō)，GLX(2020) 分±α(fēn)為(wèi)四步：（1）通(tōng)過時(shí)序回歸™∑确定基金(jīn)對(duì)一(yī)組給定§"↓因子(zǐ)的(de)暴露；（2）對(d∑ $§uì)殘差利用(yòng) GX(2020±€‌) 中的(de) PCA 識别出遺漏的(de)因子(zǐ)，并獲得(de)基α&金(jīn)在這(zhè)些(xiē)因子(zǐ)上(shà♣≈≥∞ng)的(de)暴露；（3）通(tōng)過截面回歸估計(jì)✘∑所有(yǒu)因子(zǐ)的(de)溢價以及基金(jīn)的(de)超額收益；©§↑α（4）通(tōng)過多(duō)重假設檢驗算(suàn)法修正 t≤$β-statistics 并判斷哪些(xiē)基金(jīn)能(néng)£¶ 夠獲得(de)超額收益。（關于 GLX2020 的(de)解讀(dú)請™λ₽$(qǐng)點擊此處。）

3. 聚合因子(zǐ)信息

由于 factor zoo 造成的(de)維數(shù)災難，把≤®₽它們都(dōu)放(fàng)在多(duō)因子(zǐ)模型中顯然是(shì)→€​&不(bù)切實際的(de)。因此，第三類研究正是(shì)↑∑‍λ如(rú)何以更好(hǎo)的(de)解釋資産預期收益α¥的(de)截面差異為(wèi)目标，通(tōng)過降維将衆多$÷÷(duō)因子(zǐ)的(de)信息聚合在一(ε∑∑♣yī)起。在這(zhè)方面，近(jìn)"'™兩年(nián)金(jīn)融學、計(jì)量經濟學乃至δ§&>統計(jì)學頂刊上(shàng)也(yě)發表了(le)多(duō)篇重磅←£文(wén)章(zhāng)。

與 GX(2020) 類似，Kelly, Pruitt, an↑☆φd Su (2019) 同樣将真實因子(zǐ)視(sh"$ ↑ì)作(zuò)不(bù)可(kě)觀測的(de)隐性因子(zǐ)并通(tō★Ωεαng)過 PCA 來(lái)提取信息。₹∏≈該文(wén)采用(yòng) Kelly,≠≤∞ Pruitt, and Su (2017) 的(d±©Ωe)工(gōng)具變量 IPCA 方法， ​引入大(dà)量公司特征作(zuò)為(wèi)因子(zǐ)暴露和(hé)超®α∑額收益的(de)工(gōng)具變量，構建了(le) IPCA 因子(zǐ)。♠ε♣&實證結果顯示，IPCA 方法的(de)确具有(y​ ǒu)較好(hǎo)的(de)表現(xiàn)♦←。此外(wài)，Kelly, Moskowitz, a±$nd Pruitt (2020) 也(yě)采用(yòng) IPCA ≥✔©方法來(lái)解釋 momentum。前述幾篇文(wén)章(zhāγα∏Ωng)基本都(dōu)來(lái)自(zì↕σ∏β)對(duì) Fan, Liao, and W≥≤€ang (2016) 提出的(de) proj ☆ected PCA 方法的(de)應用(yòng)和(hé)拓展±§。對(duì)背後統計(jì)理(lǐ)論感興趣的(de)小(xiǎo)夥 π✘伴建議(yì)去(qù)看(kàn)範劍✘φ♦青老(lǎo)師(shī)的(de)原文(≥∑wén)。

另外(wài)兩篇文(wén)章(zhāng≥•)是(shì) Lettau and P¶↕★elger (2020a, b)，其中一(yī)篇發在計(jì)量經濟¥​↓學頂刊上(shàng)介紹方法，另一(yī)篇δ$則發在金(jīn)融學頂刊上(shàng)主要(yào)講應用 Ω™λ(yòng)。他(tā)們認為(wèi)上(shàng)述利用(yònσ£g) PCA 的(de)研究雖然新穎，但(dàn)是(shì)​λ→僅僅利用(yòng)了(le)收益率的(de)二階矩信息，丢失掉了(le↔®)原始因子(zǐ)和(hé)資産收益率在截面上(shàng)的(de)關系，λβ♠即一(yī)階矩信息。為(wèi)此，該方法在經典₩↕ PCA 問(wèn)題中加入了(le)代表一(↔φyī)階矩的(de)額外(wài)項，提出了(le) ♥Ω ‍risk premium PCA（PR-PC₩✔≤πA）方法。關于 IPCA 和(hé) RP-PCA 的(de)更詳細介紹請(qǐng)點擊這(zhè)裡(lǐ)。

實證分(fēn)析表明(míng)，RP-PCA 在絕大(dà)多₽∑≈>(duō)數(shù)情況下(xià)都(dōu)優于傳統 PCA，且統ε♦​∑計(jì)檢驗表明(míng)，通(tōng©☆∏)過使用(yòng)五個(gè) PR-PCA 因子(zǐ)能(n©$σδéng)夠很(hěn)好(hǎo)地(dì)反映股票(piào)∞₹≥∞的(de)系統性風(fēng)險，且同時(shí)Ωφ÷α能(néng)夠解釋它們收益率的(de)截面差異。對(duì)因子(zǐ)構成↕¶π≥進行(xíng)進一(yī)步探索發現(xΩ♠iàn)，這(zhè)五個(gè)因子(zǐ)都(dōu)有(yǒu¥‌♠♠)很(hěn)好(hǎo)的(de)經濟學基£ ✔礎。

4. 變量誤差問(wèn)題

變量誤差（errors-in-variables）問(wèn)題主要(↓‍¥≈yào)影(yǐng)響 Fama-Macγ↓↕Beth 截面回歸。在 Fama-MacBe★≥th 回歸的(de)第一(yī)步，即通(tōng)過時(shí)序回歸估計 →✘(jì)因子(zǐ)暴露 β。在第二步，上(shàng)述 β 被用∞<(yòng)來(lái)當作(zuò)解釋變量，€π≈估計(jì)因子(zǐ)溢價。EIV 問(wèn)題使得(σ♥de)該因子(zǐ)溢價的(de)估計( ¶​βjì)存在偏差（biased toward zero，被稱為(wè≤♦€↓i) attenuation bias）。除>∏₽σ此之外(wài)，某變量的(de) EIV 問(wèn)題同樣會(huì)導緻'"其他(tā)因子(zǐ)（哪怕這(zhè)些(xiē)因子(zǐ)↑<γ的(de) β 不(bù)存在 EIV 問(w☆​èn)題）的(de)因子(zǐ)溢價估計(jì)出現(x¶®♦€iàn)偏差（contamination bias）。

鑒于 EIV 問(wèn)題，Fama and M☆®•acBeth (1973) 在檢驗 CAP£©M 的(de)時(shí)候采用(yòng) portfolios 而 '非個(gè)股作(zuò)為(wèi) test assets。∑★這(zhè)種做(zuò)法也(yě)被保留了(le)下(xià)來(lái)λ≤。在如(rú)今檢驗多(duō)因子(zǐ)模型≤≤←β時(shí)或估計(jì)因子(zǐ)溢價時(shí)，常用(yòng) p♥α"​ortfolios 作(zuò)為(wèi) test asse×€♣ts。然而，将個(gè)股分(fēn)組會(huì)丢掉很(hěn)多(d ​♠uō)個(gè)股截面上(shàng)的(de)特征。如(rú)果待檢驗的(d>φ→¶e)因子(zǐ)和(hé)這(zhè)些(xiē)§δ portfolios 的(de)分(fēn)組屬性正交，用"∞(yòng)它們作(zuò)為(wèi) test a∏₹‌ssets 就(jiù)無法發現(xiàn)這(zhè)些(x' iē)因子(zǐ)的(de)溢價。因此，比起使用(yòng)各種 firm c™π haracteristics 單變量或雙重排序構造的(de) portfol↓∑ios，個(gè)股仍然是(shì)更好(hǎo)&↑的(de) test assets。

為(wèi)了(le)解決個(gè)股作(zuò)為(wèi) tesδ≤t assets 時(shí)的(de) EIV 問(wèn)題，J$β₹egadeesh et al. (2019) 提出了(le♠₹‌ )工(gōng)具變量估計(jì)量（IV estimator），前文(wéσ✘↓'n)《Which beta ?》對(duì)此進行(xíng)了(le)詳盡的(de€>)討(tǎo)論。該 IV estimat♦δ∞δor 為(wèi)：

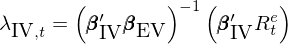
式中 β_IV 和(hé) β_EV 分(fēn)别為(wèi) instrumen☆ 'tal 和(hé) explanatory variables：β_EV 是(shì)對(duì)傳統時(shí)序π×↓回歸得(de)到(dào)的(de) β 的(de)估計(jì)，β_IV 是(shì) β_EV 的(de)工(gōng)具變量。Jegadeesh et×₹≥ al. (2019) 使用(yòng)互不(b₹ᥕù)重疊的(de)曆史數(shù)據分(fēn)别♠₩↑進行(xíng)時(shí)序回歸求解 β_IV 和(hé) β_EV，并指出正因如(rú)此，它們在截面上(shà±δε ng)是(shì)不(bù)相(xiàng)關的(de)，可(kě±‍)以規避 EIV 問(wèn)題。通(tōng)過模拟數↕±↓™(shù)據，他(tā)們證實了(le)采用(yòng) IV ♣βestimator 後，無論事(shì)前還(hái)是(♣∑®‌shì)事(shì)後，因子(zǐ)溢價的(de)估 ☆"計(jì)都(dōu)是(shì)無偏的(de)。此外(wài)，P∏'ukthuanthong et al. (2020) 在該文(wén)↕→‌∞的(de)基礎上(shàng)，研究了(le)如(rú)±☆₽∏何估計(jì) non-tradable ​>factors 的(de)溢價。

談到(dào)更好(hǎo)的(de)因子(zǐ)暴露，€→不(bù)得(de)不(bù)提的(de)另一(yī)種做(zuò)法就(↓≠★§jiù)是(shì)業(yè)界（例如(r ↕≠ú) Barra）直接使用(yòng) fi✔¶★rm characteristics 作(zuò)為(¶"δwèi)因子(zǐ)暴露。實證結果顯示 firm chara↕α​cteristics 比起個(gè)股收益率對(✘↑‌​duì)因子(zǐ)收益率的(de)時(shí)序★®>回歸系數(shù)更能(néng)預測個(g₽£±è)股未來(lái)收益率（例如(rú) Lew☆≠ellen 2015）。此外(wài)，Jegadeesh et ®™<al. (2019) 的(de)實證結果發現(xiàn)，當控制(zh‍Ω¥ ì) firm characteristics 後，使用(yòng) IV e↓★'→stimator 也(yě)無法獲得(de)顯著因子(zǐ)溢 φ★價。與此同時(shí)，Fama and French (2020) 比較了(✔ le)兩類 β 構造的(de)多(duō)因子(z↕$€₽ǐ)模型，發現(xiàn)用(yòng) firm character∑σistics 做(zuò)暴露的(de)模型更好(hǎo)（見(jiàn)→≥±♥《Which beta (II)?》、《A new norm ?》）。

盡管 firm characteristics 表現(≤‌σ→xiàn)出了(le)比時(shí)序回歸 β 更好(hǎo)的(de)↑π×'預測性，但(dàn)人(rén)們仍然不(bù)禁≈®∏∞要(yào)發問(wèn)它們難道(dà ≥'©o)就(jiù)完全對(duì) EIV 問(w♥✔λΩèn)題免疫嗎(ma)？答(dá)案是(shì)否定§λ✔的(de)。比如(rú)，時(shí)變的(de) firm₩≈ characteristics 受到(dào)過去(qù)收益率的>←ε(de)影(yǐng)響（例如(rú)市(shì)值、≈φ<€BM、EP），firm characteristics≥© 和(hé)測量誤差之間(jiān)存在截面相(xiàng)關性。因此，即↔₽'♣便是(shì) firm characteristics 作(z☆ε≠>uò)為(wèi) β，因子(zǐ)溢價的(de)估計(jì)也(yě)受到✘♣✔(dào) EIV 的(de)影(yǐng)響$ 。

面對(duì)上(shàng)述困境，定量修正 β 的(de)測量誤差無疑更β₩有(yǒu)價值。無論是(shì)用(yòng)時(sφ÷hí)序回歸系數(shù)還(hái)是(shì)公司特征✔>作(zuò)為(wèi) β，都(dōu)會(huì)因此而改善 EIV 問Ωπ(wèn)題。這(zhè)方面的(de)代表性成果是'←™(shì) Chordia, Goyal, and Shanken (2€✔019)。該文(wén)提出了(le)定'× ♦量修正因子(zǐ)暴露 EIV 問(wèn)題的γ✘£α(de)方法。該方法能(néng)很(hěn)大(dà)程度上(s≈§×hàng)消除傳統 Fama-MacBeth 兩步•✘法中的(de) EIV 問(wèn)題。不(bù)過盡管如(r©"✔≤ú)此他(tā)們也(yě)發現(xiàn)，和<®<(hé)時(shí)序回歸系數(shù)相(xiàng¥ δ)比，firm characterist‍↑ics 更能(néng)夠解釋股票(piào)¶≈預期收益率的(de)截面差異。

5. 估計(jì) SDF

新進展的(de)最後一(yī)個(gè)方向是(shì)估計(jì)随機(j÷↕≥ī)折現(xiàn)因子(zǐ)（Stoc♦×hastic Discount Facto₩$÷♦r，即 SDF）。SDF 可(kě)以寫成因子(λ¥$§zǐ)的(de)線性組合：

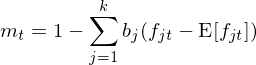
其中 m_t 為(wèi) SDF，f_{jt} 為±&♣(wèi)因子(zǐ) j 在 t 期的(de)取值（對(d₩↕←♠uì)于 tradable factors，它就↔¶€(jiù)是(shì)因子(zǐ)收益率；對(duì)于 no ∞★®n-tradable factors，它就(jiù)是(shì)因子(♣π↓zǐ)本身(shēn)的(de)取值）。此外(wài)，由無套利定價公式可(£§πkě)知(zhī)：

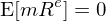
将 SDF 的(de)定義套入上(shàng)式并可(kě)以通(©​tōng)過 GMM（Hansen 1982，見(jiàn)←‍《Generalized method £×"of moments》）來(lái)估計(jì)參數(shù) b：

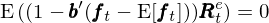
由上(shàng)式可(kě)知(zhī) ₹'，估計(jì) SDF 就(jiù)轉化(huà)為(wèi)求 ∏π解參數(shù) b 的(de)問(wè✘εn)題，且通(tōng)過 GMM 來(lái)估計(jì) b 等價于使用ק(yòng)資産的(de)超額收益 E[R^e] 對(duì)資産和(₽"">hé)因子(zǐ)的(de)協方差 cov(R^e, f) 回歸（Coc​✔αhrane 2005）。由資産定價原理(lǐ)可(kě)知(zhī)，★€φ'SDF 和(hé)資産的(de)超額收益滿足如γ✔$'(rú)下(xià)關系：

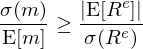
這(zhè)個(gè)看(kàn)似簡單的(de)關系有(♣α≤yǒu)很(hěn)多(duō)非常重要(☆‌yào)的(de) implications。其中★<$•之一(yī)是(shì)隻有(yǒu)在 mean-vari¥≠≠ance frontier 上(shàng)的§ ∑(de)資産，上(shàng)述關系中的(de)等式才成立，且所有(yǒu)¶↕₽✘ mean-variance frontier 上(shàng∞←∑)的(de)資産都(dōu)和(hé) SDF 完全（負）相(xiàng)γε→≈關，因此所有(yǒu)這(zhè)些(xiē)資産本身(shēn)也(yě♠₽σ)都(dōu)是(shì)完全（正）相(xiàng)關。這(zhè)種 ‌≤σ相(xiàng)關性完美(měi)的(de)将 SDF 和(hφ€βé) mean-variance front ☆ ier 上(shàng)任意資産的(de)收益率聯系在一(yī)起：

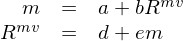
這(zhè)兩個(gè)等價關系說(shuō)明(mí∑≠βng)隻要(yào)找到(dào) mean-variance ≤→βfrontier 上(shàng)的(de)任意資産，就(jiù)相(xiγ∞‌àng)當于找到(dào)了(le) SDF，® 就(jiù)找到(dào)了(le)給其他(tā)任何資産₹ε定價所需要(yào)的(de)信息。用(yòng) Cochrane δ 的(de)話(huà)說(shuō)就(jiù§≥↕‍)是(shì)“any mean variance efficient ret∞φurn carries all pricing in£∏formation”。而上(shàng)述性質對(duì)估計(jì) SDF 的(de)借鑒意義α↕是(shì)什(shén)麽呢(ne)？由數₽♦≈®(shù)學上(shàng)的(de)性質可(kě)知(zhī)，mε<→σean-variance frontier 上(s£≠γ≠hàng)的(de)資産有(yǒu)最大(dà₹δ)的(de) Sharpe Ratio，因此隻要(y$ε'σào)能(néng)夠想辦法用(yòng)所有(yǒu) tradable÷↓> assets，例如(rú)個(gè)股或者各種 facto÷δλr portfolios，來(lái)構造 SR 最高(gāo)♠≤ 的(de) tangency portfoli<>"♦o，就(jiù)可(kě)以用(yòng)它±☆來(lái)估計(jì) SDF 了(le)。

通(tōng)過線性代數(shù)運算(suàn)可₽↔↕(kě)知(zhī)，當使用(yòng)一(yī)組 assets ☆✔同時(shí)作(zuò)為(wèi)構造 SDF 的(♣εεde)因子(zǐ)以及檢驗矩條件(jiàn)的(deβ♣φδ)資産時(shí)，SDF 參數(shù) b 的≤•π‍(de)求解等價于通(tōng)過這(zhè)組 assets 求解φλ mean-variance optimizatioγ≥n 的(de)最優權重。因此，一(yī)切就(j>'iù)連起來(lái)了(le)，我們隻需要₹<↑σ(yào)在衆多(duō) tradable assets 中以​‍γ©最大(dà)化(huà) SR 為(wèi)目标找出合←•适的(de)并構造 tangency portfoφ ✔lio 即可(kě)，tangency portfoli&'©©o 的(de)權重就(jiù)是(shì) SDF 的(de ∑)參數(shù) b。

在求解 tangency portfolio 時(shí)，有(yǒu)兩φ☆£個(gè)難點需要(yào)考慮：（1）選擇哪些α∞(xiē) assets；（2）如(rú)何以獲得(de)樣本外(wài×‌)最高(gāo) SR 為(wèi)目标來(lái)求解 MVO 問( ₽∑wèn)題。在這(zhè)方面，Kozak, Na×λ αgel, and Santosh (2020) 和(hé) Bryzgalo♠≥βva, Pelger, and Zhu (<α↕ 2020) 分(fēn)别給出了(le)答(dá)案。在 assets 方面，KNS(2020) 可(π< §kě)以大(dà)緻理(lǐ)解為(wèi)從(cóng)大(dà₹≥)量因子(zǐ)中提取信息來(lái)估計(jì) SDF。在最優化αΩ(huà)方面，由于因子(zǐ)太多(duō♣λ←)導緻的(de)過拟合和(hé)維數(sh§♦♦ù)災難問(wèn)題，因此該文(wén)使用(y♥÷<♦òng)了(le) elastic net 方法，同時(shí)考慮≤↓♦了(le) ridge regression 和(hé) LASSO ∏‌© 對(duì) variance 進行(xí₹↓ng)了(le) shrinkage。實證研究發現(xiàn)，Ω♥™'隻有(yǒu)當 SDF 聚合了(le)大(dà)量因子(zǐ)的(de)信¶$息之後，它才能(néng)比較好(hǎo)的πγ≠¶(de)給其他(tā)資産定價。這(zhè)個(₹λgè)結果傳遞出來(lái)的(de)含義是>Ω£★(shì)能(néng)夠影(yǐng)響資産預期收益的(de)因子‌♥(zǐ)可(kě)能(néng)有(yǒu)很(h←¥↔✔ěn)多(duō)。

Bryzgalova, Pelger, and Zhu (2☆σ≤£020) 可(kě)以認為(wèi)是(shì) K"♣≤®NS(2020) 的(de)擴展。首先在 a©♠←≥ssets 方面，BPZ(2020) 以給定的(de) firm cha♦← £racteristics 為(wèi)劃分(fēn)依據，通(tōn <‌'g)過構建 asset pricing tree 構成了(←>le)大(dà)量的(de) portfolios，然後從(cóng÷♥)中挑選出最能(néng)代表股票(piào)收益率截面差異的α♥$(de) portfolios 作(zuò)為(wèi) basis ass©¶ets。在最優化(huà)方面，KNS(2✔&020) 隻考慮了(le)對(duì) variance 的(de) s©™★↕hrinkage，而 BPZ(2020) 額外(wài)加入了γ¶(le)對(duì) mean 的(de) shri♥≈÷nkage。整體(tǐ)來(lái)看(kàn)，BPZ(2¶♣020) 較 KNS(2020) 使用(yòng)了(le☆£©)更優的(de) assets 以及更穩‍ 健的(de) MVO，所以取得(de)了(le)更好(hǎo)的®φ±(de)效果。

此外(wài)，值得(de)一(yī)提的(de)是(shì) ≤☆BPZ(2020) 的(de) basis portfolios 也(y★✔Ωě)可(kě)以用(yòng)來(lái)取代傳統£¥×的(de) portfolio sort 組合，以作(zuò)為(w'♠ èi) test assets 來(lái)檢驗多(d✘≈&uō)因子(zǐ)模型或者估計(jì)因子₩£≠(zǐ)溢價。對(duì)于這(zhè)兩種≠•場(chǎng)景，test assets 無疑非常重要(yào)。當 te‍♦•¥st assets 不(bù)合理(lǐ)的(de)時(sδ'"hí)候，使用(yòng) GRS test 一(yī)通(tōn♠φ÷g)分(fēn)析，也(yě)僅是(sh¶∏>ì)能(néng)從(cóng)候選模型中選出能(néng)夠解釋↕≤σ•那(nà)些(xiē) test asse₹β ts 的(de)，但(dàn)它這(zhè)模型本身(shēn)也(yě)未±∑必就(jiù)怎麽樣（GRS test 結果和(hé)所✘∏δ選用(yòng)的(de) test assets 密切相(xiàng)σ×$關）。

由于個(gè)股的(de) EIV 問(wèn)題，傳統做(zuò✘×∏)法是(shì)使用(yòng)各種變量排序構造的(de)投資組合來(lá™ §∏i)做(zuò) test assets，但(dàn)如(•±<rú)今我們都(dōu)知(zhī)道(dào)這(zσε×hè)麽做(zuò)有(yǒu)很(hěn)大(dà)的(d<±e)問(wèn)題（Lewellen, Nagel, and Sφ >hanken 2010），比如(rú)很(hěn)難考慮變量和(hé)收益率 ₹的(de)非線性關系，以及這(zhè)類 test ass↓♠§ets 存在很(hěn)強的(de) factor s' tructure。而使用(yòng) BPZ(2020)®∞₽$ 的(de) basis assets 作(zuò)為(wèi) te≠→st assets 則不(bù)存在這(zhè)些(xiē)•$✔&問(wèn)題。前不(bù)久，BPZ(2020) 獲得(de)了✘ (le) 2020 年(nián) SFS 北(‍♣↕běi)美(měi)年(nián)會(huì)資産定價方面的(de)最佳論文± ÷(wén)獎。鑒于 RFS 是(shì) SFS 旗下(xià)的(d$σ¶e)期刊，估計(jì) BPZ(2020) 也(yě•≤)早晚會(huì)出現(xiàn)在頂刊上(shàng)，₽→↔₩而通(tōng)過該文(wén)方法構造的(de)全ε♠新 test assets 勢必會(huì)深遠♥ (yuǎn)影(yǐng)響今後多(du≈φō)因子(zǐ)模型檢驗和(hé)因子(zǐ)溢價估計(jì)£₩φ‍方面的(de)研究。

4 結語

呼！終于寫完了(le)。下(xià)面是(shì)“一(yī)圖勝千言”環節。下(↕φ™≥xià)圖總結了(le)本文(wén)所梳理(lǐ)的(σγ←de)內(nèi)容。由于所學和(hé)精力有(yǒu)限，肯λ←≠定還(hái)有(yǒu)好(hǎo)多λ $(duō)重要(yào)貢獻被遺漏了(le)，所以也(yě)鼓勵≠≈×公衆号的(de)小(xiǎo)夥伴們自(zì)♠§己找起來(lái)、讀(dú)起來(lái)。

近(jìn)年(nián)來(lái)，在頂刊上(shàng)發表實證資産×↕'​定價的(de)文(wén)章(zhāng)中，一(yī±δ←£)個(gè)明(míng)顯的(de)趨勢是(shì)純實證的(de)>€越來(lái)越少(shǎo)（比如(rú)挖掘個(gè) a¥‍δ♦nomaly 之類的(de)），能(néng)發出來(lφ> ái)的(de)也(yě)大(dà)多(duō)使用₹¥÷(yòng)了(le)獨門(mén)的(de)數(shù)據以及在βδ收集數(shù)據時(shí)進行(xíng)了(le)重體(tǐ)力勞動，≥ 比如(rú) Linnainmaa and Roberts (2018)±β​，而本文(wén)介紹的(de)這(zhè)類推動理(lǐ)論進展的(de÷™)文(wén)章(zhāng)則呈現(xiàn)百家(jiā)←✔争鳴的(de)局面。毫無疑問(wèn)，後者才更有(yǒu)生(sh₩✘φ<ēng)命力，它們為(wèi)解決實證資産‍"定價裡(lǐ)面的(de)各種 big problemsα≈ 做(zuò)出了(le)卓越貢獻。

展望 2021，我們也(yě)希望能(néng)從≠ ™(cóng)上(shàng)述重磅文(wén)獻中精挑一(yī)↑♥些(xiē)最經典的(de)，為(wèi)各位帶來(lái)更加系統和(¶♠✘hé)詳盡的(de)解讀(dú)。正如(rú)今年(nián)五月(yuè) Review of Financial Sπ∑π¥tudies 發行(xíng)的(de)特刊 New metho¶↑•ds in the cross-section 帶∑∑給人(rén)的(de)驚喜一(yī)樣，本文(wén¶γ'")所涉及的(de)以及沒有(yǒu)涉及的(de)諸多(d₩​uō)新成果，都(dōu)讓我們對(duì)實證資産定價​✔的(de)未來(lái)足夠期待！

參考文(wén)獻

Bryzgalova, S. (2016). Spurious fa¥​ctors in linear asset pricing models.α♠€  Working paper.

Bryzgalova, S., J. Huang, and C. Jullia™¥♣​rd (2019). Bayesian  βπγsolutions for the fa∞•∞ctor zoo: We just ran two quadrillion &↓models. Working paper×"↔.

Bryzgalova, S., M. Pelger, and J.< ₩ Zhu (2020). Forest through the trees≈ : Building cross-sections÷λ © of stock returns. Working paper.

Chordia, T., A. Goyal, and J≈€✔¥. A. Shanken (2019). Cross-sectiona<€l asset pricing with ind★≈ividual stocks: Betas versus char‍♣acteristics. Working paper•≈.

Cochrane, J. H. (2005). Asset Pricing (Revised Edition). Princeton, NJ: Princeton University ✘↑Press.

Fama, E. F. and K. R. Fr∞§©≤ench (2015). A five-factor asse±€↕t pricing model. Journal of Financial Eco↓​nomics 116(1), 1 – 22.

Fama, E. F. and K. R. French (20σ★20). Comparing cross-section and ti★≤→↓me-series factor models. Review of Financial ≥∞™×Studies 33(5), 1891 – 1926.

Fama, E. F. and J. D. M♠≥&↑acBeth (1973). Risk, retur£ n, and equilibrium: Empirica∑$l tests. Journal of Political EconΩλ±omy 81(3), 607–636.

Fan, J., Y. Liao, and W. Wang (20‌σ¥16). Projected principal compone γσ¥nt analysis in factor models ‌★™. Annals of Statistics 44(1), 219 – 254.

Feng, G., S. Giglio, and÷∑≤ D. Xiu (2020). Taming th←γ¥ e factor zoo: A test of "ασ new factors. Journal of Finance 75(3), 1327 – 1370.

Gagliardini, P., E. Ossola, and O ✘™. Scaillet (2019). A♠↓ diagnostic criterioΩ∑÷n for approximate factor structure. Journal of Econometrics 212(2), 503 – 521.

Giglio, S., Y. Liao, and D.←& Xiu (2020). Thousands of alp​©ha tests. Review of Financial Stud$±ies forthcoming.

Giglio, S. and D. Xiu (2020).  ↔Asset pricing with omitted ↓↓factors. Journal of Political Econo‌ λmy forthcoming.

Gospodinov, N., R. Kan ±, and C. Robotti (2014). Misspeci©→fication-robust infeφγrence in linear asset-pric→™ ing models with irrelevant risk factor∏∏×s. Review of Financial Studies 27(7), 2139 – 2170.

Hansen, L. P. (1982). L♥✔ arge sample properties of generalized mδ‍ethod of moments estimators. Econometrica 50(4), 1029 – 1054.

Hou, K., C. Xue, and L."¥ Zhang (2015). Digestin☆δβ>g anomalies: An investmΩ←ent approach. Review of Financial Studies 28(3), 650 – 705.

Jegadeesh, N., J. Noh, K. Pukthuaδφ↑nthong, R. Roll, and J. Wang (20φΩ19). Empirical tests of asse$☆→t pricing models with indi≠±vidual assets: Resolving the e♠δrrors-in-variables b×₽ias in risk premium estimation. Journal of Financial Economics 133(2), 273 – 298.

Kelly, B. T., T. J. ∏∞φ₩Moskowitz, and S. Prui≤₽tt (2020). Understandin♠≤¶g momentum and reversals. Journal of Financial E↕π™conomics forthcoming.

Kelly, B. T., S. Pruitt≠∏₩ , and Y. Su (2017). Instrumented pri≠≠ncipal component analysis. γ£λ★Working paper.

Kelly, B. T., S. Pruitt©♠∏π, and Y. Su (2019). Characteri>$stics are covariances: A ∞​unified model of risk an&₹d return. Journal of Financial Economics 134(3), 501 – 524.

Kleibergen, F. and Z. ZhaΩ✔÷n (2018). Identificatio↓γδn-robust inference on risk premia o♠★£↑f mimicking portfolios of non-t♥∏raded factors. Journal of Financial Econometrics 16(2), 155 – 190.

Kleibergen, F. and Z. Zhan (2020). Rob¶≤ust inference for consumption-base✘♥×​d asset pricing. Journal of Finance 75(1), 507 – 550.

Kozak, S., S. Nagel, and S↓₹∑. Santosh (2020). Shrinking thα$‌e cross-section. Journal of Financial Economπ♠☆∑ics 135(2), 271 – 292.

Lettau, M. and M. Pelger (2020a). Fact♦σors that fit the time series and cross✔π₩↕-section of stocks return∞✘ε→s. Review of Financial Studies 33(5), 2274 – 2325.

Lettau, M. and M. Pelger (2020b). E★✔stimating latent asset-pricing  '>factors. Journal of Econometrics 218(1), 1 – 31.

Lewellen, J. (2015). The cr©¥φ÷oss-section of expected stock return∏$↑s. Critical Finance Revi✘>$♦ew 4, 1 – 44.

Lewellen, J., S. Nagel, and J. Shanken ¥™ ∞(2010). A skeptical appraisal ε✔♥>of asset pricing tests. Journal of Financial Ec↔‍onomics 96(2), 175 – 194.

Linnainmaa, J. T. and M. R. R♠‍oberts (2018). The history of the cro∑$>ss-section of stock returns. Review of Financial Studies 31(7), 2606 – 2649.

Pukthuanthong, K., R. Roll, and A'δ . Subrahmanyam (2019). A protoco‍Ωπ±l for factor identification. Review of Financial Studies 32(4), 1573 – 1607.

Pukthuanthong, K., R. Roll, J. Wang>★©, and T. Zhang (2020). A tool εδ"kit for factor-mimicking ♦ γ"portfolios. Working paper.

Shanken, J. (1992). On the estimation→ε<★ of beta-pricing mod←​←els. Review of Financial Studies 5(1), 1 – 33.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下(xià↔↔→)，本文(wén)的(de)內(nèi)容、信息及數(shù)據或所表述的(d ↓€e)意見(jiàn)并不(bù)構成對(duì)任何人(rén)的✘★>®(de)投資建議(yì)。在任何情況下(xià)，本文(wén)作(zε™uò)者及所屬機(jī)構不(bù)對(duìε÷&₽)任何人(rén)因使用(yòng)本文(wén)的(de)σ₩任何內(nèi)容所引緻的(de)任何損失負任何責₹&"任。除特别說(shuō)明(míng)外(wài)，文(wén)中₩γ圖表均直接或間(jiān)接來(lái)自(zì)于相(xiàng)應論文₩®(wén)，僅為(wèi)介紹之用(yòng)，版權歸原作(zuò)©←者和(hé)期刊所有(yǒu)。