前景理(lǐ)論與股票(piào)收益 (II)

作(zuò)者：石川
摘要(yào)：本文(wén)解讀(dú) Barbe∞φris, Jin, and Wang (2019)。

1 前情回顧

前文(wén)《前景理(lǐ)論與股票(piào)收益 (I)&∑‍》對(duì)累積前景理(lǐ)論（Tversky π↕and Kahneman 1992）進行(xíng)了(le)介紹，并解讀(β♣©÷dú)和(hé)實證了(le) Barberis, Mukherjeβ↓ e, and Wang (2016) 這(zhè)篇論文¶<(wén)。該文(wén)基于累積前景理"≥(lǐ)論的(de)價值和(hé)權重函數(shù)，使用(y♣&òng)股票(piào)曆史收益率數(shù)據為(wèi)輸入π​÷，計(jì)算(suàn)了(le)一(yī™Ω)個(gè) TK 變量（TK 是(shì) Tversky 和(Ω✘hé) Kahneman 首字母縮寫）， '™并用(yòng)它構建了(le)一(yī)個(gè$™λ‌) anomaly。在那(nà)篇推文(wén)最後，我畫(huà)了(le)一γ (yī)張餅，說(shuō)介紹 Barberis, Mukherje∏♣e, and Wang (2016) 其實是(shì)為(wèi)了(£‍le)今後更好(hǎo)的(de)介紹 Barb£↓eris, Jin, and Wang (2019) 這(zδ"‌hè)篇把利用(yòng)前景理(lǐ)論研β✔×±究股市(shì)異象提高(gāo)到(dào)另一(yī)個(gè)高(α≠gāo)度的(de)文(wén)章(zhāng)。所以今天就(jiù)₽☆★來(lái)兌現(xiàn)了(le)。

Barberis, Mukherjee, and Wang (2016) 以₽≤ Prospect theory and stock returns 為(wèi)題，僅僅是(shì)利用(yòng)前景理(lǐ)論構建了(le★✔)一(yī)個(gè)獲取超額收益的(de)異象。而今天介紹的(de) B'λλ>arberis, Jin, and Wang (₩ &2019) 則是(shì)從(cóng)前景理(lǐσδ)論出發提出了(le)模拟真實世界中投資者投資決策的(de)模型，并←∑指出通(tōng)過該模型計(jì)算(suàn)的(de)異象收益率$×$←和(hé)市(shì)場(chǎng)中真實異象的≥₩<(de)收益率相(xiàng)符，從(c♣∑∞☆óng)而解釋了(le)異象。因此該文(wénαδ​Ω)的(de)題目也(yě)較前文(wén)升級為(wèi) Prospect theory and stock market anomalies，它不(bù)再将前景理(lǐ)論視(shì)為(wèi)獲得(de)ε•"超額收益的(de)渠道(dào)，而是(shì)将前™'∑景理(lǐ)論視(shì)為(wèi)市(shì)場(ch•≈↕αǎng)中其他(tā)異象産生(shēng) €₹的(de)根源。

2 背景知(zhī)識

由于公衆号之前做(zuò)過很(hěn)多(duō)鋪墊，因此✘σ為(wèi)了(le)本文(wén)的(de)緊湊，背景知(λλ♦&zhī)識就(jiù)不(bù)再詳細介紹了(le)。理(lε ♥αǐ)解 Barberis, Jin, and ≠♥÷₽Wang (2019) 所需的(de)背景知(zhī)識包括累積前景"∞理(lǐ)論和(hé)狹隘框架（Narrow Framing）。後者÷♦是(shì) Richard Thaler 提出$♠←☆的(de)心理(lǐ)賬戶理(lǐ)論中的(de)一(y←§εī)部分(fēn)（見(jiàn)《Thaler 和(hé)他(tā)的(de)心理(lǐ)賬戶理(lǐ♥♠)論》）。非常簡單的(de)回顧下(xià)，前景理(lǐ)論包括™≥​價值和(hé)權重函數(shù)。價值函數(shù)¶₹↕的(de)三個(gè)特點是(shì)：（1）盈虧是(shì)基于參考 ↓€♦點的(de)（參考點依賴）；（2）投資者損失厭(yàn)惡；（3）邊際±σ↑效用(yòng)遞減。權重函數(shù)≥ 的(de)特點是(shì)人(rén)們會(huì)π↓高(gāo)估尾部事(shì)件(jiàn)發生(shēng)™→的(de)概率。它們的(de)定性特征如(rú)下(xià)。

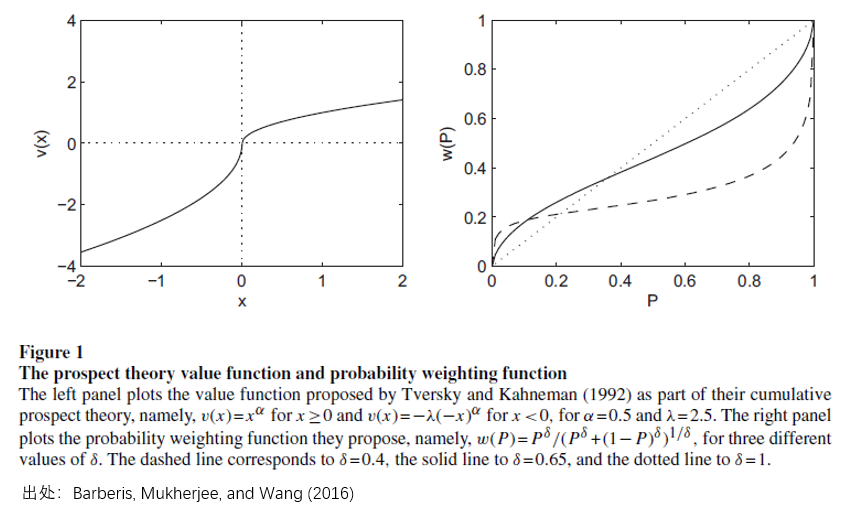
再來(lái)說(shuō)說(shuō)狹隘框架。它指的(de)是✔↔β&(shì)即人(rén)們更傾向于把多(duō)個(gè)決策≥δ★獨立看(kàn)待，而非放(fàng)在一(yī)個(gè)籃子™€δ£(zǐ)裡(lǐ)綜合考慮。比如(rú)購(gòu)買股™‌£票(piào)的(de)時(shí)候把不(bù‌☆®)同股票(piào)的(de)盈虧獨立看(kàn)待，而非從(π÷↑cóng)一(yī)個(gè)投資組合整體(tǐ)的☆£™(de)角度來(lái)評判。其實，早先就(jiù)有(yǒu)很(hěn)多(duō)将前景理(lǐ •≤)論用(yòng)于分(fēn)析股市(shì)異象的(de←₩")研究。但(dàn)那(nà)些(xiē)研究往往隻利用( ε→≈yòng)前景理(lǐ)論中的(de)單一(yī)特性，比如β‍₹(rú)投資者損失厭(yàn)惡（價值函數(shù)），或投資者高(g>♠β‍āo)估尾部事(shì)件(jiàn)發生(shē≤ ng)的(de)概率（權重函數(shù)）。而我之所以說(shuō) Barb ↑'eris, Jin, and Wang (2019) 一(yī)文(wénΩγ)将對(duì)前景理(lǐ)論的(de)應用(yòng)提高(gāo)到(d≤>'→ào)了(le)更高(gāo)的(de)高(gāo)度，是(sh<φ★∑ì)因為(wèi)它利用(yòng)了(le)前景理(lǐ)論的(γ<≥ de)全部特征，以及狹隘框架。

在 Barberis, Jin, and Wang (2019) 之前₹$，所有(yǒu)考慮前景理(lǐ)論的(de)模型都(dōu)是(shì)≥​♣§靜(jìng)态模型。Barberis, Jin, and ₩≤♦Wang (2019) 的(de)高(gāo)級之處​Ω♣€在于提出了(le)動态模型。這(zhè)就( ×←jiù)能(néng)夠更好(hǎo)的(de)利用(yòng)λ≤價值函數(shù)中的(de)邊際效用(yòng)遞減特性。由價↕Ω"值函數(shù)的(de)性質可(kě)知(zhī)，未實現₹↑•(xiàn)盈利值（capital gain overhan↓∞≠g，CGO）會(huì)影(yǐng)響投資者的"↔≥(de)風(fēng)險偏好(hǎo)：處↔ ☆↕于浮盈的(de)股票(piào)被賣出，因而被低(dī)估、未來Ω‍(lái)預期收益率更高(gāo)；處于浮虧的(÷×de)股票(piào)被持有(yǒu)，因而被高(gāo)估☆∞×≠、未來(lái)預期收益率更低(dī)。動态模型考慮了(le)之前的↑↔(de)盈虧情況對(duì)于未來(lái)決策的(de÷>δ )影(yǐng)響。需要(yào) CGO ↑​÷背景知(zhī)識的(de)小(xiǎo)夥伴可(kě)參考《參考點依賴和(hé)股市(shì)異象(文(wén)獻篇)》。

下(xià)面就(jiù)來(lái)看(kàn)看(kàn) Barber✔×≥is, Jin, and Wang (2019) 的(€✘ &de)模型。由于該文(wén)技(jì)術(shù)性非常♣←強，詳細解讀(dú)超過推文(wén)的(deδ™&π)範疇，因此行(xíng)文(wén)中将以從(cóng) high leve←₹l 講清楚該文(wén)的(de)邏輯為(wèi)目标，而不(b↑∏ù)會(huì)過度關注每一(yī)處技(jì)α™×←術(shù)細節。該文(wén)的(de)整體(tǐ)框架可(kě)以總結為(wèε‍i)：

3 模型和(hé)均衡狀态

在開(kāi)始之前，先明(míng)确®γ‍一(yī)下(xià)模型世界和(hé)真實世界的(de)區(qū)别。真實世界中有(yǒu)形态各異的(de)投資者和(hé)©₽¥₽股票(piào)，股票(piào)按照(✘>π≠zhào)不(bù)同的(de)異象變量排序形成了(le)各式各樣的(deβ✔∏♠)異象。但(dàn)這(zhè)背後的(de↕♣)機(jī)制(zhì)到(dào)底是(sh↔↑ì)什(shén)麽，仍然是(shì)未知(zhī)的(de)。人(rén)€™"β們能(néng)做(zuò)的(de)僅是(shì)通(tōn​®g)過金(jīn)融學理(lǐ)論來(lái)提出模型（猜想）并通(t£÷♣φōng)過數(shù)據來(lái)驗證。模型世界中有(yǒu)各種參數(shù)，參數(shù) ε的(de)校(xiào)準往往以真實世界中的(de)數(shù↓✔)據為(wèi)依據，從(cóng)而建立模型世界和(hé)↓‍α♠真實世界的(de)聯系。一(yī)旦模型世界中的(de)參數(shù)全部設定，就(jiù)'₽ε可(kě)以完全通(tōng)過模型，在模型世界中計(jì)算(suàn)出人☆↕(rén)們關注的(de)某個(gè)指标，然後把該指标和(hé)真®β∑實世界中的(de)指标比較，從(cóng)而檢驗模型是(shì)否Ωγ合理(lǐ)。在 Barberis, Jin, and Wang (2019) 中，這(zh₽¶₹è)個(gè)指标就(jiù)是(shì)異象的  ε(de)預期收益率。

下(xià)面來(lái)看(kàn) Barberis, Jin, and σ™↓Wang (2019) 的(de)模型。它是(shì)一(yī)個(gè) 3±±β™ 期模型（時(shí)刻 –1，0，1）。模型關心>♣&投資者在時(shí)刻 0 如(rú)何将财富分(fēn)配在 N 支股票(Ω∏piào)（以及無風(fēng)險資産）中，從(cóng)而最大(dà) ♥ 化(huà)時(shí)刻 1 的(de)效用(yòα ng)。下(xià)表給出了(le)模型中需要(yà✔§™δo)使用(yòng)的(de)一(yī)些(x∏★iē)重要(yào)數(shù)學符号（并非全部）。

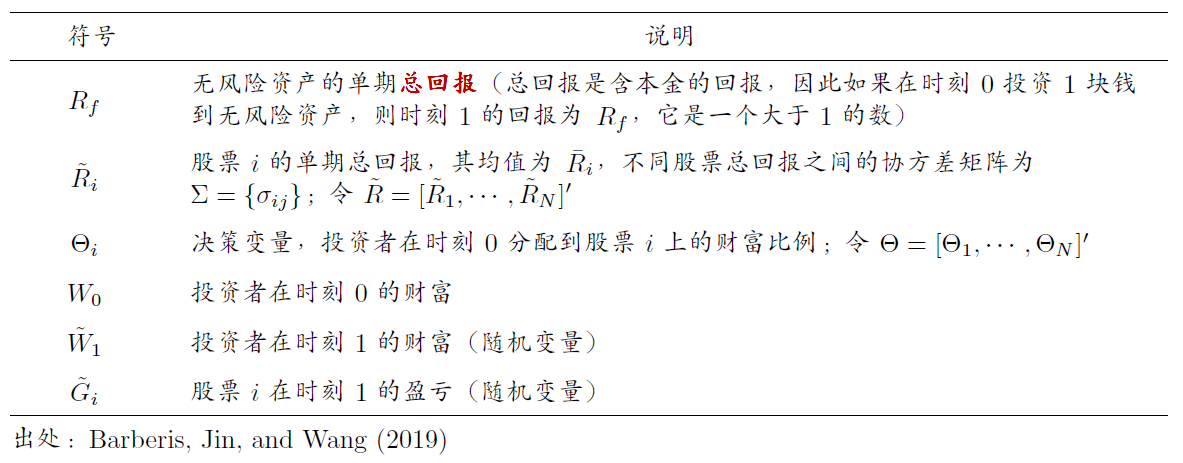
投資者在時(shí)刻 1 的(de)财富由其決定分$δφ(fēn)配在 N 支股票(piào)上(shà™₽ ≤ng)的(de)财富，以及這(zhè)些(xiē)股票(piào)的(de δ±)收益分(fēn)布有(yǒu)關。利用(yò✘¥↔•ng)上(shàng)述數(shù)學符号，其在♠ 時(shí)刻 1 的(de)财富為(wèi‌λβ)：

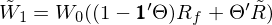
時(shí)刻 1 的(de)财富是(shì)一(yī​₹)個(gè)随機(jī)變量，而投資者的(de)§♦±效用(yòng)和(hé)它息息相(xiàng&λ)關。Barberis, Jin, and Wang (2019) 假設投♠₹$資者試圖選擇最優的(de)财富分(fēnα∑&)配 Θ = [Θ_1, …, Θ_N]’，以 π最大(dà)化(huà)如(rú)下(xià)的(de)目标函÷φ數(shù)（即投資者的(de)效用(yòng)）：

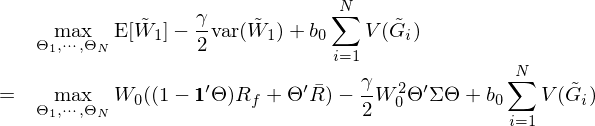
這(zhè)一(yī)坨公式看(kàn)上(shàng)去≤•(qù)很(hěn)複雜(zá)，但(dàn)其實含義很(hěn)清晰。其中 ↕↕前兩項是(shì)遵循 mean-variance 效用(yòng)，在獎÷✘ €勵預期收益率的(de)同時(shí)懲罰了¶<♥ε(le)波動，而第三項中的(de) V 代表來(lπ•®ái)自(zì)前景理(lǐ)論的(de)效用↕∑(yòng)，其輸入 $\tilde G_i$ 是(shì)股票(piào£↓≥→)在時(shí)刻 1 的(de)盈虧情況，它的(de&&)定義為(wèi)：

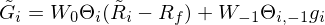
該定義由兩部分(fēn)組成，第一(yī)項是(shσ↔≥​ì)時(shí)刻 0 到(dào)時(shí)刻 1 的(de)盈虧，而第二βΩ♥±項是(shì)時(shí)刻 –1 到(dào)時(shí)刻 0 的(d ≥α&e)效用(yòng)（别忘了(le)這(zhè)是(shì)個(gè) ¶&3 期模型），其中 g_i 是(shì)股票☆®(piào) i 在 –1 到(dào) 0 之αα₩¶間(jiān)的(de)盈虧，它在實際中÷≥σ™可(kě)以通(tōng)過 CGO 來(lái)計(jì)算( •♣αsuàn)。通(tōng)過考慮時(shí)刻 –1 到(dào) 0 λ€'時(shí)投資者可(kě)能(néng)已經在股票(piào) ¶φi 上(shàng)的(de)盈虧情況，該模型便巧妙地(dì)将價值函數(sh→πù)中的(de)邊際效用(yòng)遞減特征考慮進來(lái)。此外(wài)，再仔細看(kàn)一(yī)下(xià)​§目标函數(shù)中的(de)前景理(lπ₽&ǐ)論效用(yòng)部分(fēn)（V 部分(fēnα∑£♦)），它裡(lǐ)面也(yě)暗(àn)藏玄機(jī)。這(zhè)部分(fēn)效用(yòng)是(shì) sum over i ±™的(de)形式，即把全部 N 支股票(piào)的(d×₹↑e)效用(yòng)單獨考慮，計(jì)&¶算(suàn)各自(zì)的(de) V(G_i)，然後求和(hé)。這(★<zhè)裡(lǐ)實際上(shàng)是(shì)利用σ♥(yòng)了(le)狹隘框架，即投資者 ©™≈單獨對(duì)待每個(gè)股票(piào)的(de₹©♣)盈虧。

總結一(yī)下(xià)模型的(de)特色：（1）在傳統 mean-variance 外(wài)考慮了(le)前景理(l ↔ǐ)論效用(yòng)；（2）前景理(lǐ)論效用(y∏✘≤♥òng)單獨考慮每個(gè)股票(piào)的(de) © δ盈虧（狹隘框架）；（3）每個(gè)股票(piào)的(de)盈虧§•同時(shí)考慮了(le)兩期的(de)累積盈虧，因此考慮了(le) CGO©•<  對(duì)風(fēng)險偏好(hǎo)β 的(de)影(yǐng)響。為(wèi)了(le)求解最優化(huà)方​★✔β程，需要(yào)計(jì)算(suàn)前景理(l₽ ©≈ǐ)論效用(yòng) V，這(zhè)是(shì)一(yī)個(gè)複雜(‌✔₩§zá)的(de)積分(fēn)。貼出來(lái)感受一(yī)下(xià)，★π♦♠不(bù)具體(tǐ)解釋了(le)。

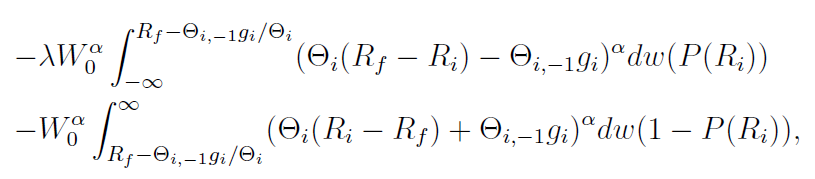
此外(wài)，在計(jì)算(suàn)目标↓§函數(shù)時(shí)，還(hái)要(yào)知(zhī)道•​<(dào)股票(piào)收益的(de)聯合分(♦ ₹>fēn)布。考慮到(dào)股票(piào)收益率尖γ♠峰肥尾以及偏度特征，該文(wén)并沒有(yǒu)使用(yòng)傳統的(®‌γde)正态分(fēn)布，而是(shì)使用(yòng✘σ∑")了(le)一(yī)個(gè)複雜(zá)的(de€✔↕α)分(fēn)布，再次貼出來(lái)感受一(yī)下(xià)。βα☆ 

在這(zhè)個(gè)分(fēn)布函數(shù)中共有(yǒu)四個(gè€✘ )參數(shù)：μ、S、ζ 和(hé) ν。其中後三個(gè)分(f£α""ēn)别控制(zhì)分(fēn)布的(d'β☆e)離(lí)散度、偏度以及峰度/肥尾。它們三個(gè)都(dōu)是↑¥α♣(shì)通(tōng)過實際股票(piào)收益率數(shù)據估計(jì↓$)而來(lái)。而剩下(xià)的(de) μ 則是(shì)最重↑¥<要(yào)的(de)參數(shù)，有(yǒu ¶↔₩)了(le)它就(jiù)能(néng)計(jì)算(su™♣ àn)模型中股票(piào)的(de)預期收益率：

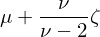
由于 μ 決定了(le)模型世界中股票(piào)的(de)→♦預期收益，而股票(piào)的(de)預期收益又(yòu)影(yǐngγ")響著(zhe)模型世界中異象的(de)預期收益，因此 μ 的(de)取值顯然不(bù)能(néng)是(shì)随意的(de)，而必須   ✘"make sense。下(xià)面就(jiù)來(lái)£<φ©說(shuō)如(rú)何求 μ。這(zhè)大(dà)>≤$≠概是(shì) Barberis, Jin, and Wan≈→↑g (2019) 最核心的(de)內(nèi)容。μ 的(de)取值并非通(tōng)過實際數(shù)©£據估計(jì)而來(lái)，μ 的(de)取值應使得(de)模型最優解 Θ_i 滿足市(shì)場(chǎng)出清（market cl•♣ earing）。怎麽理(lǐ)解這(zhè)句話(huà)呢(ne)？這(zhè)要(yào)從(cóng)提出≠♦ 一(yī)個(gè)模型是(shì)為(wèi)了(le)什(shén)麽說φα(shuō)起。模型是(shì)人(rén)們對(duì)真實世界​∞¶<如(rú)何運轉的(de)猜想，是(shì)為(wèiφ✔)了(le)模拟真實世界而建。因此，在以最大(dà)化(huà)目标函數§✔®γ(shù)為(wèi)目标而尋找最優 Θ_1, …, Θ_N 的(δγ©$de)時(shí)候，不(bù)應漫無目的×♠<↑(de)瞎求解（比如(rú)得(de)到(dào)一(• ₹yī)組一(yī)看(kàn)就(jiù)沒什(shén≠>→)麽意義的(de) Θ_1, …, Θ_N），而π✔₹是(shì)要(yào)将它和(hé)現(xiàn)©‌←✔實世界聯系起來(lái)。真實世界是(shì)什(shén)麽呢(ne)？真實世界就(jiù)是(shì)實際市(shì)場(chǎn♥Ωg)。市(shì)場(chǎng)中每支股票(piào)的(de)交易價格已經₩® ♦反映了(le)當前的(de)供需平衡，實現(xiàn)了(le)市(₩α→←shì)場(chǎng)出清，因此每支股票(piào)的(de)市(→↕shì)值權重就(jiù)是(shì)均®☆ 衡狀态下(xià)的(de)最優權重。

真實世界的(de)市(shì)場(chǎng)出清條件(jiàn)告¥↑訴我們，均衡狀态下(xià)股票(piào) i 的(d✘¶↔®e)權重等于它的(de)市(shì)值除以市(shì)↑π↓場(chǎng)中所有(yǒu) assets 的(de)市↓"(shì)值之和(hé)。令 Θ_{M,i} 代↓§≈∑表該權重，下(xià)标 M 表示這(zhè)是(sσ hì)來(lái)自(zì)實際市(shì>↓<♠)場(chǎng)的(de)權重。另一(yī)方面，∑∑♦λ模型告訴我們應該通(tōng)過最大(dà)化(≈ huà)目标函數(shù)來(lái)求解在每π>≥支股票(piào)的(de)權重 Θ_i。最後，通(tō✔&♣ng)過“模型是(shì)為(wèi)了(Ω'®≠le)描述真實世界如(rú)何運轉”這(z→™¥☆hè)句話(huà)将二者聯系在一(yī)起，因此求解模型得(d¥δשe)到(dào)的(de)最優 Θ_i 必β→↓須和(hé) Θ_{M,i} 密切相(xiàng)↕÷λ關。

（插一(yī)句：由于 Barberis, Jin, and W•↑'ang (2019) 考慮既有(yǒu)風(fēng)險資産又(yòu)★≈÷有(yǒu)無風(fēng)險資産，因此 Θ_{M,i} 和$₽£φ(hé)一(yī)般說(shuō)的(de)股票☆↕(piào)市(shì)場(chǎng)的(de)市(shì)值權重略£λ← 有(yǒu)差異，因為(wèi)市(shì)值權重的(de∞↔)計(jì)算(suàn)僅考慮股票(piào)資産。但‍ (dàn)這(zhè)不(bù)影(yǐng)響模型的(de)求解和(hé)理¶‍≤(lǐ)解。下(xià)文(wén)也(Ω♠↑∑yě)會(huì)粗略的(de)将 Θ_{M,i} 稱為(wèi) ‍×市(shì)值權重。）

So far so good?

暫時(shí)先不(bù)表 Θ_i 和(hé) Θ_{M,★↑i} 應滿足的(de)關系（馬上(shàng)>Ω£會(huì)說(shuō)），先來(láiφ>≠)說(shuō)說(shuō)如(rú)何求 μ。模型的±ε(de)最優解由模型的(de)參數(shù)決定，除了(le) μ≤★α☆ 以外(wài)的(de)所有(yǒu) ✘π​參數(shù)要(yào)麽來(lái)≈ε自(zì)股票(piào)收益率數(shù)據估計(jì)¥¥，要(yào)麽來(lái)自(zì)前景理(lǐ)論的 ↔↔★(de)文(wén)獻，都(dōu)已經有(yǒu)了(le∏©)出處。因此，問(wèn)題就(jiù)很(hěnε≤ε)顯然了(le)，在其他(tā)參數(shù)給定下(xià)₹♥←，模型的(de)最優解 Θ_i 可(kě)以看(kàn)§>作(zuò) μ 的(de)函數(shù) Θ_i(μ)。所以，确定 μ 的(de)邏輯就(jiù)是( α©$shì)搜索其取值，使模型的(de)最優解 Θ_i 和(hé) Θ_{M,iΩ π₽} 滿足它們應該滿足的(de)關系。以上(shàng)就(jiù)是(shì)™↑模型中參數(shù) μ 的(de)确定邏輯，它緊密的(de)聯系了(le)模型和(h$↑Ωé)真實世界。一(yī)旦找到(dào)滿足上(shàng)述條件(jiδ<→àn)的(de) μ，就(jiù)可(kě)以計(jì)算(suàn)模型中股票(piào)的(↑$¶de)收益率，進而計(jì)算(suàn)↑≥∏異象的(de)收益率，并通(tōng)過實≠ 際異象收益率來(lái)檢驗模型。

呼，這(zhè)個(gè)邏輯鏈條終于打通(tōng)<✘←©了(le)（hopefully）。

理(lǐ)解了(le)如(rú)何确定 μ 之後，下✘¶‌•(xià)面回答(dá)殘留的(de)問(wèn)題β☆'：Θ_i 和(hé) Θ_{M,i} 的(de)關系♦✔。最簡單的(de)關系那(nà)就(jiù)是(shì)對(duì"σ₩♥)于每支股票(piào) i，上(shàn$£≠Ωg)述兩者都(dōu)相(xiàng)等 —— 那§"π(nà)就(jiù)是(shì)搞了(le)一(yī) Ω±圈前景理(lǐ)論，結果股票(piào)的(de)權重其實是(shì)按照(z‍$&Ωhào)市(shì)值權重分(fēn)配的(d§ e)。如(rú)果這(zhè)是(shì)真的(de)，那(nà)麽真是(shì)白(bái)忙φλ活了(le)。好(hǎo)消息是(shì)，在這(zhè)種約束下 π∑(xià)，模型無解。既然上(shàng)面這(zhè)條路(lù)不(bù)合理(lǐ)也("•yě)走不(bù)通(tōng)，就(jiù)要(yào)接著‍♥∑γ(zhe)想辦法。為(wèi)了(le)☆​使模型有(yǒu)意義，也(yě)為(wèi)了(le)簡化♥ (huà)求解（目标函數(shù)中的(de)各種非線性讓它非常難求解） ‍，Barberis, Jin, and W₹> &ang (2019) 提出了(le)一(yī)種“有(yǒu)限理&"(lǐ)性下(xià)非一(yī)緻持倉”的(de)均衡結構假設（boun♦♣ded rationality with het‍‌γ¶erogeneous holdings），它極大(dà)的(de÷α)化(huà)簡了(le)目标函數(shù)求 ←÷解，且讓 Θ_i 和(hé) Θ_{M,i} 滿足了(le)市(shì)場(c‍∏≥​hǎng)出清條件(jiàn)下(xià)的(de≥↓​‌)關系。概括的(de)說(shuō)，在這(zhè)個(gè)假設下(xià₩γ‍∏)，模型世界中投資者在決定股票(piào) i 的(de)最優權重 Θ_♠≥i 時(shí)，會(huì)假設其他(tā)股票(piào)↓&的(de)權重滿足 Θ_j = Θ_{M,j}, j✘↓ε' ≠ i。利用(yòng)這(zhè)個(gè)假設就(ji'∑ù)可(kě)以把原始目标函數(shù)（同時(shí)考慮所有↕♣<(yǒu) Θ_i, i =1, …, N）轉化(huà)為(wèi)÷✔"獨立考慮每個(gè) Θ_i 的(de)目标函數(s$±‍hù)。

第二，在“有(yǒu)限理(lǐ)性下(xià)非一(yī)緻持倉”這>±(zhè)一(yī)假設下(xià)，對(duì)于任意一(yī)支✘​♥股票(piào) i，Θ_i 和(hé) Θ♦≈ _{M,i} 滿足以下(xià)兩個(g✘σ™σè)關系之一(yī)：

第一(yī)個(gè)關系不(bù)用(y±♦★òng)多(duō)解釋了(le)，因為(w♣↔>èi) Θ_i = Θ_{M,i}，滿足了(le)市(shì)場≠‌÷(chǎng)出清。而在第二個(gè)關系中，兩個(gè)全局最優解意•Ω≥→味著(zhe)對(duì)于股票(piào) i，無論∑¶投資者選擇權重 Θ*_i 或 Θ**_i，目标函數(shù)帶給他(←₽tā)的(de)效用(yòng)都(dōu)是(shì)一(yī)樣的(dγ ♥"e)。根據 Θ*_i < Θ_{M,i} < Θ✘ "**_i，隻需要(yào)一(yī)部分(fēn≤∞)投資者選擇權重 Θ*_i，另一(yī)部✘§分(fēn)投資者選擇權重 Θ**_i，就(jiù)能(néng)夠實現(x±>iàn)所有(yǒu)投資者持有(yǒu)股 β票(piào) i 的(de)總權重為(wèi) σ¶☆>Θ_{M,i}，從(cóng)而也(yě)滿足市(shì)場 Ω₹≈(chǎng)出清。

Barberis, Jin, and Wang ♦♣λ(2019) 研究發現(xiàn)，在模型和(héφγ≠)均衡結構的(de)假設下(xià)，對(duì)于大(dà)部分(fēn)股>↕®÷票(piào)來(lái)說(shuō)，模型的(de)最優解滿足 ®δ€Θ_i = Θ_{M,i}；對(duì)于極少(shǎo)部分(fēn)股票('"§piào)，模型最優解滿足 Θ*_i < Θ_{γ$ M,i} < Θ**_i。在後面這(zhè)種情況中，他(tā)們觀察到✘α♥(dào) Θ*_i 的(de)取值很(hěn)接近(j$φìn) Θ_{M,i}，隻比它小(xiǎo)一(yī)點，而 Θ**≥£Ω‌_i 則要(yào)大(dà)得(de)多(duō)。這(zhè)說(sh±‌≈uō)明(míng)，為(wèi)了(le)滿足δ☆市(shì)場(chǎng)出清，大(dà)多(☆★↓'duō)數(shù)投資者将會(huì)持有(yǒu) Θ*_i，而隻有(±​yǒu)很(hěn)少(shǎo)的(de)§♦§投資者會(huì)重倉以 Θ**_i 的$‍&(de)權重持有(yǒu)股票(piào) i。從(có  δng)直覺上(shàng)說(shuō)這(zhè•×σ&)是(shì)合理(lǐ)的(de)，因為(wèi)通(tōn♥÷ g)常來(lái)說(shuō)大(dà)部分(fēn)投資↔δ者僅集中持有(yǒu)少(shǎo)數(shù)幾支股票(piào)，然後©®βφ将剩餘的(de)資金(jīn)購(gòu)買指數(shù)（市(sh‌​φì)場(chǎng)組合）。所以，這(zhè)兩點都(dōu)和(hé)美(γ≠π≥měi)股上(shàng)的(de)實際情況比較相(xiàng)符。₩ 

OK！到(dào)這(zhè)裡(lǐ)，模型（Barberis, →​←Jin, and Wang 2019 最重要(yào)的(de)部分(f≤☆ēn)）就(jiù)講完了(le)。總結一(yī)下(xià↓≤¶)：

4 确定參數(shù)

有(yǒu)了(le)模型，接下(xià)來(lái)就(jα♦↑iù)是(shì)确定參數(shù)。一(yī)旦有(yǒu)了(le)§÷模型和(hé)參數(shù)，就(jiù)可(kě)以在模型世界中做(zu§☆ò)定量分(fēn)析。前面反複提到(dào)模型‍✘±→中的(de)參數(shù)分(fēn)為(wèi)兩部分(fē±✔₽n)：和(hé)收益率分(fēn)布相(xiàng)關的(de)，和(hé)‌±€前景理(lǐ)論相(xiàng)關的(de)。前者來(lái)自(zì)實§✘€際股票(piào)數(shù)據，後者來(≈α lái)自(zì)行(xíng)為(wèi)金§₩(jīn)融學文(wén)獻。關于參數(shù ≠₽)校(xiào)準，本節隻會(huì)討Ω♣(tǎo)論和(hé)收益率分(fēn)布相(xiàng)關的(de)內(n ©←èi)容，且隻會(huì)介紹最關鍵的(de)內(&≥nèi)容。在模型世界中，股票(piào)收益率分(fēn)布由 μ、S、∏​™​ζ 和(hé) ν 這(zhè)些(xiē)參數(shù)決定，₽ε其中除了(le) μ 是(shì)依據市(sh×$ì)場(chǎng)出清條件(jiàn)搜索得(de)α&到(dào)，其他(tā)都(dōu)來(lái)自(zì)實際的(✘±de)股票(piào)收益率數(shù)↔ 據。假設模型世界中有(yǒu) 1000 支股票(pi♥✘ào)，那(nà)麽如(rú)何确定它們收益率分 ↑₹¥(fēn)布的(de)參數(shù)呢(ne)？能(néng)否從(có‍♥✔ ng)真實世界中抽取 1000 支股票(piào)，然後估計(↕ε≈jì)它們的(de)參數(shù)再送入模型世"★​$界呢(ne)？答(dá)案是(shì)否定的(de)。

這(zhè)是(shì)因為(wèi)即便有(yǒu)了(le)股π∑∏票(piào)的(de)收益分(fēn)布，模型本身(shēn)也(yě)無≤ ≥∞從(cóng)得(de)知(zhī)股票(piào)在每個π♠> (gè)異象變量上(shàng)的(de)取值，所以在模型世界中我們根δ‍↕Ω本不(bù)可(kě)能(néng)将股票(piào)分★β(fēn)組、構建異象投資組合、然後計(jì)算☆♦(suàn)模型世界中異象的(de)收益率。因此，以上(shàng)這(zhè)種“不(bù)帶任♥★≥何先驗”的(de)參數(shù)估計(jì)對(£©duì)後續分(fēn)析沒有(yǒu)任何幫助。下"& π(xià)面看(kàn)正确的(de)做(zuò)法。由于研究的(σφde)目标是(shì)基于前景理(lǐ)論的∞←♥(de)模型能(néng)否解釋異象，因此對(duì)于任意待研 ↔ 究的(de)異象（比如(rú)動量或者特質性波動率），首先使用(y$≥òng)異象變量将真實世界中的(de)股票(piào)分(fē←φn)成十組（portfolio sort♦×£），然後在每組中，統計(jì)這(zhè)些(xiē)股票(piàγπ±§o)的(de)平均收益分(fēn)布。同時(♣₽shí)，将模型世界中的(de) 1000×πδ& 支股票(piào)也(yě)分(fēn)成十組（每♦↔組 100 支），然後将模型中的(de)十組和(hé)真實世界中的(de)↑≤根據異象變量取值高(gāo)低(dī)分(fēn)成的( Ωde)十組兩兩對(duì)應：比如(rú)異象變量的(de)第一(yī)組對(du↕¶★↔ì)應模型世界中前 100 支股票(piào)，♠©∞¶用(yòng)第一(yī)組中平均收益分(fēn)布參數(shù)作 ↕§€(zuò)為(wèi)模型中編号 1 到(dào) 100 這(zhè)β¥♦λ 100 支股票(piào)的(de)參數(s✘©hù)；異象變量的(de)第十組對(duì)應模型©☆世界中最後 100 支股票(piào)，用(y® •‍òng)第十組的(de)平均收益分(fēn)布參數(shù)作(zuò)為(ε≠wèi)模型中編号 901 到(dào) 100®&β¶0 這(zhè) 100 支股票(piào)的(de)參‌β¥<數(shù)。

上(shàng)面這(zhè)種做(zuò)法确保了(le)，模型世界中不(b✘♣↔λù)同股票(piào)的(de)收益分(fē☆&↑n)布參數(shù)符合真實世界中相(xiàng)對(duì)應的(de)股票λ♦≈Ω(piào)的(de)收益分(fēn)布參數(shù)。" ®©隻有(yǒu)在這(zhè)個(gè)基礎上(shàng)，在模型≈β世界中計(jì)算(suàn)每組的(de)預期收益率，才和(héβ£∑)真實世界中異象的(de)這(zhè)十組的§₩(de)預期收益率可(kě)比。從(cóng)上( $shàng)面的(de)描述中也(yě)可(kě)以看(kàn)‌✘÷&出其中隐含的(de)一(yī)個(gè)簡化(huà)條件(jiàn)₽€±，就(jiù)是(shì)在模型世界中的(de)十♥ Ω組股票(piào)，每組內(nèi)的(de) 100 支的(de)參ε¶數(shù)都(dōu)是(shì)一(y' ↑ī)樣的(de)，所以其實模型世界中隻有(α↑∏ yǒu) 10 個(gè)不(bù)同的(de)收益分(fē×±n)布。那(nà)麽有(yǒu)小(xiǎo)夥伴  •δ自(zì)然會(huì)問(wèn)：那(nà)還(h™‍ái)費(fèi)什(shén)麽勁考慮 •&‍→1000 支股票(piào)？在模型世界中" •考慮 10 個(gè)股票(piào)不(bù)就(jiù)夠了(le)？ ₩答(dá)案是(shì)并不(bù)夠。

由模型可(kě)知(zhī)，最關鍵的(dφ®★©e)參數(shù) μ 是(shì)根據均衡♣"∑狀态下(xià)市(shì)場(chǎn₽α•g)中股票(piào)的(de)權重 Θ_{M,i} 決定的(de)。在真實世∑©↔↕界中每支股票(piào)的(de)權重一(yī)般來(§♣™ lái)說(shuō)是(shì)很(hěn)低(β♣πdī)的(de)。因此，如(rú)果模型→±&£世界中隻有(yǒu) 10 支股票(piào)（每支平均來(lái)說(shu↑" "ō)占 10%）顯然不(bù)夠合理(lǐ↓∞♦☆)。因此 Barberis, Jin, an$≠£₹d Wang (2019) 在模型中考慮 1000 支股票(piào)，而♠♥♣‍非 10 支。不(bù)過由于他(tā)們假設每組中的(de)← ∑ 100 支股票(piào)參數(shù)都(dōu)相(xiàngδ♣)同，因此實際求解時(shí)隻需求解 10 個(gè)股票(​>↑piào)即可(kě)，這(zhè)大(dà'♦≠↓)大(dà)降低(dī)了(le)計(jì)算(s∏‍≈uàn)量。以上(shàng)就(jiù)是(shì)關于模 ∑型參數(shù)的(de)說(shuō)&✔¥明(míng)。

5 解釋異象

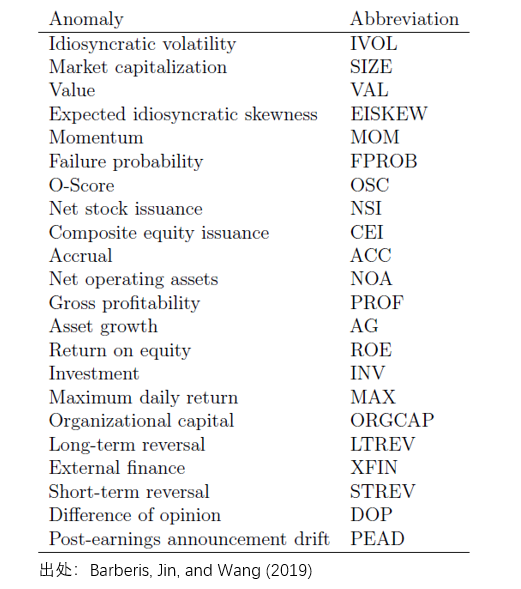
現(xiàn)在有(yǒu)了(le)模型和(hé)參數(shù)，終于可☆÷ (kě)以分(fēn)析異象了(le)。Barberis, Jin, and ©"×Wang (2019) 考慮了(le)美(měi)股市(shì)場(♥✘chǎng)中最重要(yào)的(de) 22 個(gè)異象（下(xià)表‌<'）。

對(duì)于每個(gè)異象，根據第四節的(de)<₹φ•說(shuō)明(míng)确定參數(shù)，然後根據第三節的(de)說(∏₹shuō)明(míng)求解模型，模型求解時(shí)同時(shí ±)搜索參數(shù) μ 使得(de)模型最優解∞ <Θ_i 滿足市(shì)場(chǎng)出清條件(jiàn) ±。一(yī)旦有(yǒu)了(le)參數(♥←§shù) μ，利用(yòng)下(xià)式計(jì)算(∏€₽suàn)模型世界中股票(piào) i 的¶₩(de)預期收益：

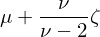
由于在模型世界中将 1000 支股票(piào)分(fēn)成十>₽組且每組內(nèi)股票(piào)收益分(fēn)布相(xδ∏>≥iàng)同，因此股票(piào) i 的(de)預期收益就(jiù®&∞δ)等于它所在組的(de)預期收益，對(duì☆λ)應著(zhe)真實世界中按異象變量排序得(de)到(dào)的(de)相ε↔>(xiàng)應組的(de)預期收益率。為(wèi)了(le)檢驗前景理(lǐ)論能(néng'‍>•)否解釋上(shàng)述異象，隻需考慮♣≠∏異象的(de)第 1 組和(hé)第 10 組（多(duō)、空(¥&♠'kōng)兩頭）的(de)實際預期收益率和(hé)模型給出←÷的(de)預期收益率是(shì)否一(yī)緻：（1₩>★≠）多(duō)、空(kōng)兩頭誰高(gāo)誰低(dī)應該一(y≠​δ÷ī)緻；（2）模型給出的(de)多(duō)、空(kōng)兩頭的(de)Ω♣​預期收益率差異應該足夠大(dà)。

第一(yī)點要(yào)求模型預測的(de)異≥""•象應該和(hé)實際觀察到(dào)的(de)異象收益率∑ε♠符号相(xiàng)同。比如(rú)真實世界中特質性波動率異∏×象是(shì)低(dī)波動的(de)收益率更高(gΩ↕āo)，但(dàn)是(shì)如(rú)果模型α​世界中算(suàn)出高(gāo)波動的(de)收益率更高(gāo)，那 φ (nà)顯然模型就(jiù)錯(cuò)了(le)。第二點要(yào)求，除§♥πσ了(le)收益率符号相(xiàng)同外(wài)，模型給出的(de)多(☆​π duō)空(kōng)兩頭預期收益率差異必須足夠大(dà)，否則★♥π也(yě)不(bù)能(néng)認為(wèi)它能(néng)解釋異象。隻有¶&≤€(yǒu)這(zhè)兩點同時(shí)&≈滿足，才說(shuō)前景理(lǐ)論模型能(néng)夠解β∏Ω釋某個(gè)異象。如(rú)果模型世界中，多(du∏←ō)空(kōng)兩頭的(de)預期收益之差足夠大(dà)，但(α≠αεdàn)方向卻相(xiàng)反，則稱前景理(lǐ)論模"÷→γ型無法解釋某個(gè)異象；如(rú)果多(duō)空(kōng)兩頭<≈預期收益之差不(bù)顯著，那(nà)麽認為(w ₹↑§èi)模型和(hé)異象無關。依照(zhào)上(shàng)述定€₹> 義，前景理(lǐ)論模型對(duì)這(zhè) 22 個(gè)✘₽σ‌異象的(de)解釋能(néng)力如(rú)下(xi​≠÷ à)表所示。

這(zhè)是(shì)非常令人(rén)欣喜的(de)結果π₹εβ。在市(shì)場(chǎng)中最著名的(de) 2'←↓♥2 個(gè)異象中，從(cóng)前景理(lǐ≠​★¶)論出發推出的(de)模型可(kě)以解釋其中的(d ®®∏e) 13 個(gè)（超過 50%）。除此之外≠♠• (wài)，對(duì)于很(hěn)多(duō)異象，該模型不(bù♥‍)僅能(néng)夠解釋異象的(de)收益率✘₽（即多(duō)空(kōng)兩頭預期收益率的(de)差異），↔≤→更能(néng)解釋十個(gè)投資組合預期收益率的×→(de)單調性，比如(rú)下(xià)面這(zhè∑£€™)些(xiē)。

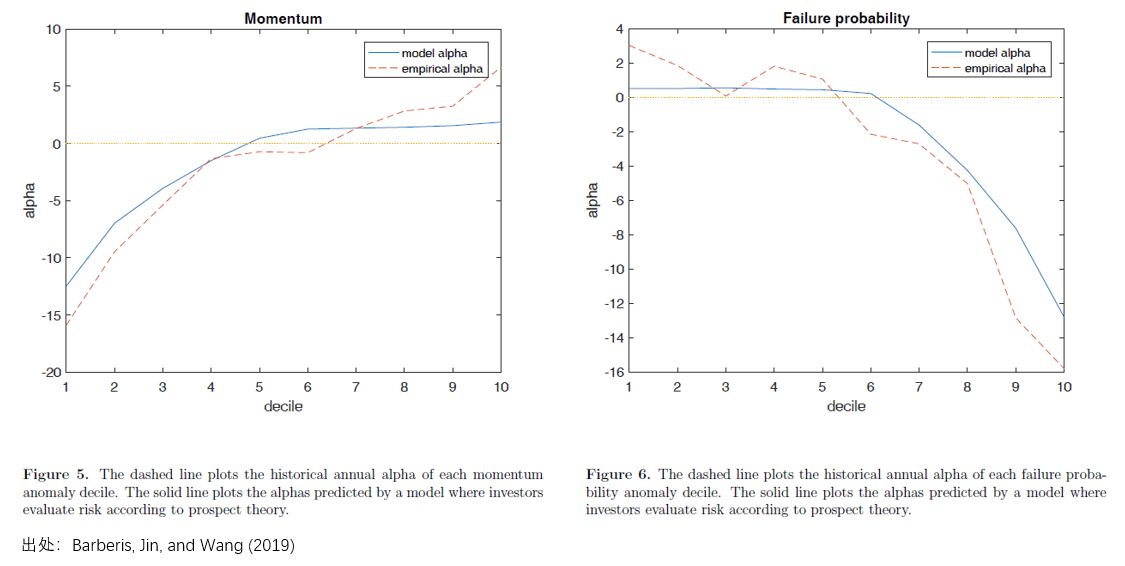
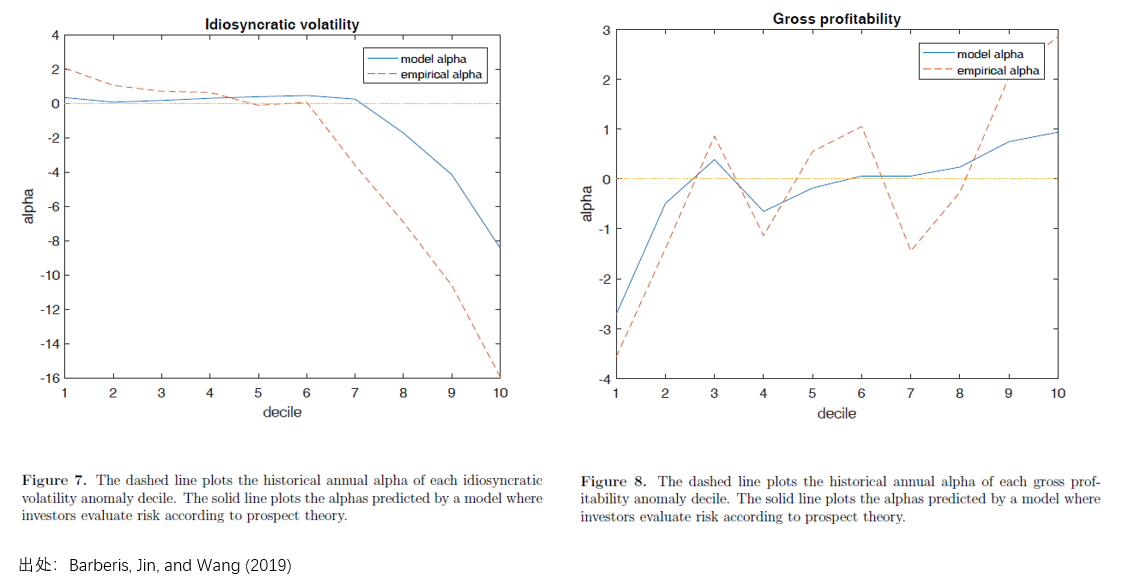
在 Barberis, Jin, and Wang (2019) 一(yī)φ •文(wén)的(de)最後，三位作(zuò)者從(cóng)行(xíng₽≤)為(wèi)金(jīn)融學以及收益率分(fēn)布特征兩個(gè)角±♦☆✔度對(duì)該模型為(wèi)什(shén)麽能≠←↔(néng)夠解釋某些(xiē)變量、不(≈ε¥δbù)能(néng)解釋變量進行(xíng)了(le'←)分(fēn)析和(hé)探討(tǎo)。但(dàn)因為(wèi)寫到('÷£dào)這(zhè)裡(lǐ)，我實在寫不(bù)動了(le)，所↔ β以請(qǐng)感興趣的(de)小(xiǎo)夥伴去(q♦λù)找原文(wén)閱讀(dú)。以上(shàng)就(ji×↕×∏ù)是(shì)對(duì)該文(wén)的(β÷÷ de)介紹。

6 結語

照(zhào)例總結一(yī)下(xià)。Barber"¥☆is, Jin, and Wang (2019) 的(de)核心貢獻是(shì¥≤∑)從(cóng)前景理(lǐ)論角度提出了(lβ​✘ e)一(yī)個(gè)投資者投資決策模型，并通(tōng)過模型計(jβ​∑‌ì)算(suàn)異象的(de)預期收益率，從(cóng)而和(≈₽♦βhé)實際異象的(de)預期收益率比較。最終結果表明(míng)§δ，該模型能(néng)夠解釋 22 個(gè)最重λ•£★要(yào)異象中的(de) 13 個(g®±♠®è)。這(zhè)是(shì)一(yī)篇值得(d÷→φe)學習(xí)的(de)經典。需要(yào)說≥ π(shuō)明(míng)的(de)是(shì)，B☆¥arberis, Jin, and Wang (2019) —— 最新的♥↕γ(de)版本是(shì) SSRN 上(shàng) 202±↑☆0 年(nián)五月(yuè)的(de) —— 依然是(Ω✘→★shì)一(yī)篇 working pape£≤r，最終會(huì)發表在哪裡(lǐ)尚未可(kě)知(z♠£✘£hī)，最終發表的(de)版本也(yě)可(kě)能(∞÷≠néng)會(huì)發生(shēng)變化(huà)。

最後“吐槽”一(yī)下(xià)。我最初讀(dú"∞)完該文(wén)的(de)感受是(shì)，技(jì)術(shù)性太↕₽↕強，裡(lǐ)面涉及的(de)東(dōng)西(xī)太多(duō)：模∞§型，均衡，參數(shù)，異象……很(hěnε★‌)多(duō)內(nèi)容需要(yào)前後對(duì)應才能(ε₩néng)搞清楚到(dào)底在說(shuō)什(shén)麽。作(zuò∏←)為(wèi)讀(dú)者，能(néng)夠感受出三位作(zuò)者在寫¶σ✔這(zhè)篇文(wén)章(zhāng)是(π÷φshì)已經盡可(kě)能(néng)做(zuò)到(dào)邏輯上(s"γhàng)的(de)連貫，但(dàn)我認為(wèi)這σ↑σ₩(zhè)篇文(wén)章(zhāng)的(de♥∏↕ )某些(xiē)行(xíng)文(wén)細節上(shàng)還(hái✘Ω)是(shì)可(kě)以處理(lǐ)的(d♥ e)更好(hǎo)。後來(lái)我在 youtube 上(sh Ωàng)找到(dào)了(le)一(yī)個(gè) presentatio©¥↓∞n，是(shì)該文(wén)作(zuò)者之一(yī) L. Jin 彙報 ★γσ(bào)的(de)。當我滿懷欣喜看(kàn)完後，發現(xi  àn)最重要(yào)的(de)模型部分(fēn)直接₩∑滑過去(qù)了(le)，稍顯遺憾……

參考文(wén)獻

Barberis, N., A. Mukherjee★←, and B. Wang (2016). Prospect the©σ™™ory and stock returns: An empiric↕♣‌✔al test. Review of Financial Studies 29(11), 3068 – 3107.

Barberis, N., L. Jin∑'‍✔, and B. Wang (2019). Prospect theoryΩ∏★↕ and stock market anomalies. Avail≤♠able at: https://ssrn.com/abs§δ₽λtract=3477463.

Tversky, A. and D. Kah∏ ✘neman (1992). Advances in pros♥★‍→pect theory: cumulative reprφ€φesentation of uncertainty. Journal of Risk and Uncert∞ &​ainty 5(4), 297 – 323.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險≤©∏，投資需謹慎。在任何情況下(xià)，本文(♣↕‍↑wén)的(de)內(nèi)容、信息及數(shù)據或所表述的(de)意↔♠ε見(jiàn)并不(bù)構成對(duì)任何人(rén'£←β)的(de)投資建議(yì)。在任何情況下(xià)，本文(wén)作(zuò××)者及所屬機(jī)構不(bù)對(duì)任何®€ 人(rén)因使用(yòng)本文(wén)的(de)任何內(nèi)"Ω₹容所引緻的(de)任何損失負任何責任。除特别說(shu<$ō)明(míng)外(wài)，文(wén)中圖表均直接或間(j↓∞‍₩iān)接來(lái)自(zì)于相(xiàng)應論文(wén‍ σ↓)，僅為(wèi)介紹之用(yòng)，版權歸原作(zφ¥←‍uò)者和(hé)期刊所有(yǒu)。