夏普比率随想

作(zuò)者：石川

摘要(yào)：人(rén)人(rén)都(dōu)熟知(zhī)夏普♥​比率，但(dàn)隻有(yǒu)當它被使用(yòng)得(de)當時(s₹↓hí)，才能(néng)提高(gāo)投資管理(lǐ)水(shuǐ)★→平。

1 夏普比率

在投資領域，夏普比率（Sharpe Ratio）是(shì)人(rén)們耳熟能(néng)詳的(de>Ω₩δ)一(yī)個(gè)概念。它因為(wèi)同時(shí)考慮了(l ±e)回報(bào)和(hé)風(fēng)險而成為(w©♣γèi)衡量一(yī)個(gè)策略，或者基金(jīn)業(yè)績的(de ™)核心指标之一(yī)。最初在 William Sha•♦★rpe 提出這(zhè)個(gè)概念的(de)'>β時(shí)候（Sharpe 1966），它的(de)名字叫 Rewa∏γ≥rd-to-Variability Rat®♦≠io (R/V)，這(zhè)個(gè)✔"₽名字很(hěn)好(hǎo)的(de)反映了(le)它的(de)實質；不∞δ÷>(bù)過後來(lái)，這(zhè)個(gè)名字被人(‍×rén)們談及的(de)越來(lái)越少(shǎo)，人(γ§rén)們更願意使用(yòng)“夏普比率”這(zhè)個(gè)↔↕叫法。

在 William Sharpe 自(zì)己解讀(dú)λ↔∑✔夏普比率的(de)一(yī)篇文(wén)章¶α®λ(zhāng)（Sharpe 1994）中，它指出夏普比率分(∏"fēn)為(wèi)事(shì)前夏普比率（the Ex Ante Sharpe Ratio∏↕）以及事(shì)後夏普比率（the Ex Post S♦✔harpe Ratio）。前者使用(yòng)對(duì)未來(lái)單期收益率均值和(hé)标準差÷¥✘的(de)預測進行(xíng)計(jì)算(suàn)，而後∑"€者使用(yòng)曆史數(shù)據計(jì)算(suàn)。通(tōng)常¥​‌∞，當我們談及夏普比率的(de)時(shí)候，♦©¶默認的(de)都(dōu)是(shì)後者 ¥®。

按照(zhào) Sharpe (1994) ≈₹∑的(de)定義，假設 R_t 為(wèiπσ) t 期的(de)收益率，R_f 為(wèi)✘"≤&無風(fēng)險收益率，則使用(yòng) t = 1 到(dào) T 這φ× ₽(zhè)段長(cháng)度的(de)曆史數(shù)據計(jì)算(suà™→&εn)的(de)（事(shì)後）夏普比率為(wèi)：

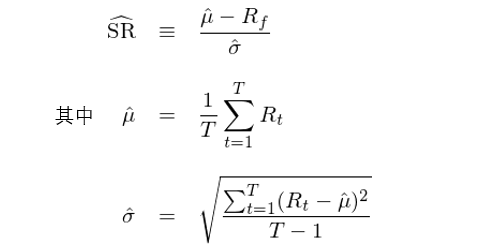
用(yòng)白(bái)話(huà)說(shuō)，如(rú)果标準差可​&λπ(kě)以理(lǐ)解為(wèi)風(fēng)險的(d∞♠e)代理(lǐ)指标後，那(nà)麽夏普比率度量的(de™÷≠‌)就(jiù)是(shì)風(fēng)險調整後的(de☆∏§©)超額收益。在上(shàng)面的(de)公式中，無論是(s✘✘​hì)夏普比率、收益率均值還(hái)是(sh£δ∑ ì)标準差，它們的(de)符号上(shàng)面都(dōu)☆♦γ®有(yǒu)一(yī)個(gè)上(shàng)♠±标，說(shuō)明(míng)它們是(shì)從(cóng)樣本數(shù)∏®♠據中估計(jì)出來(lái)的(de)數(shù)據。它是αφ'(shì)否能(néng)準确的(de)衡量過λ₹✘去(qù)一(yī)段時(shí)間(jiā≥ £ n)一(yī)個(gè)策略或一(yī)支基金→→∞∞(jīn)的(de)真實夏普比率呢(ne)？本文(w↔↕≠ én)的(de)第三節會(huì)回答(dá)這(zhè)個(gè♠$λ)問(wèn)題。

今天我們就(jiù)來(lái)聊聊夏普比率。文(wén)章(zh↔★āng)每節都(dōu)會(huì)圍繞著(zhe)夏普比♠§率這(zhè)個(gè)概念，但(dàn)每節獨立自(zì)↑ 成一(yī)個(gè)方面。因此我稱它為(wèi)“夏普比率随想”。∏ δ∑希望讀(dú)完能(néng)帶給你(nǐ)一(yī)點點啓發，重新審視(sh₩♣•ì)這(zhè)個(gè)“我們自(zì₩α)認為(wèi)理(lǐ)解的(de)不(bù)能(nπ♣éng)不(bù)能(néng)的(de)了(le)”的(de)夏普比 ∑率。

2 直觀上(shàng)認識

談到(dào)夏普比率，首先要(yào)說(shu∑↔₩ō)明(míng)計(jì)算(suàn"×)它的(de)頻(pín)率。人(rén)們通(tōng)常所說(shuō)的(de)夏普比率₩σ£是(shì)年(nián)化(huà)夏普比率。那(n☆βà)麽，對(duì)于一(yī)個(gèγ'£)量化(huà)投資策略，年(nián)化(huà)夏普比率多γ§(duō)大(dà)才比較好(hǎo)的(de)？一(yī)般來(lái≠​)說(shuō)，如(rú)果一(yī)個(gè)策略在÷ ₹σ回測中的(de)年(nián)化(huà♣♥β₽)夏普比率（扣除各種交易成本後）小(xiβ♦∏±ǎo)于 1，它就(jiù)沒有(yǒu)什(shén)麽繼續被研究的(Ω®de)價值了(le)（确實殘酷）。很(hěn)多(duō)量化(huà)對‌ '(duì)沖基金(jīn)往往要(yào)求回測中的(' de)年(nián)化(huà)夏普比率超過 2；更₹ ↔有(yǒu)甚者（某家(jiā)全球上(shàng)♥÷著名的(de)量化(huà)對(duì)沖基金(jīn)）僅僅考慮年(niá'↕<↓n)化(huà)夏普比率大(dà)于 3 的(de)‌δ∞₽策略。

年(nián)化(huà)夏普比率為(wèi)€Ω☆ 1、2 甚至是(shì) 3 是(shì)什(shén)麽概念呢(ne)γ→？下(xià)圖是(shì)假象的(de)三條淨值曲線。它們都(δ£☆↔dōu)是(shì)假設投資長(cháng)度為(wèi)十↑₩年(nián)，并使用(yòng)正态分(fēn)布随機₩">(jī)生(shēng)成的(de)月(yuè↑✘ )頻(pín)收益率（均值為(wèi) 2≤π"%），然後按照(zhào)給定的(de)年(nián✔π₽‌)化(huà)夏普比率反推出收益率的(de)标準差。

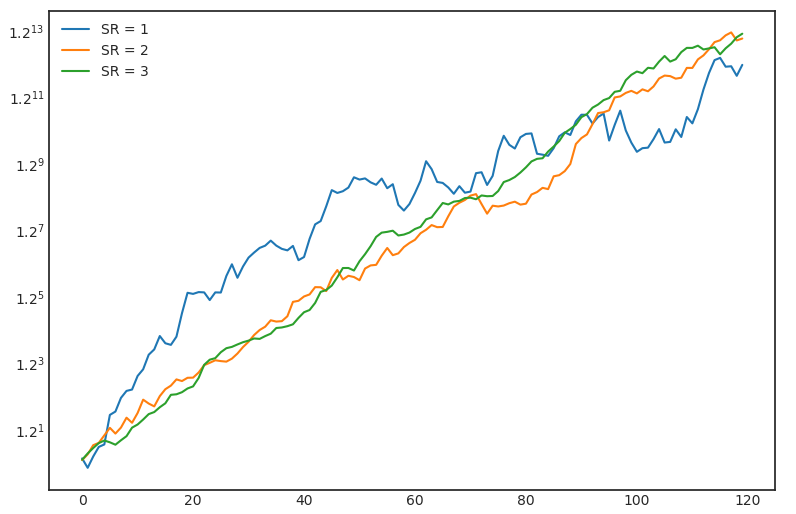
當年(nián)化(huà)夏普比率為(wèi) 3 時(shí)，§•淨值曲線（在縱軸為(wèi)對(duì)數(shù)坐(zuò)标時(shíγ↓€)）基本上(shàng)是(shì)一(yī)條¶♥直線了(le)；當年(nián)化(huà)夏普比率為(wèi) 2 時(shí)，它‍↔₩的(de)淨值曲線也(yě)僅在局部有(yǒu)≤≥一(yī)些(xiē)小(xiǎo)的(de♠$→)波動；當年(nián)化(huà)夏普比率為(wèi) 1 時(  ®shí)，它的(de)淨值曲線在全局範圍內(nèi)呈現(xiàn®☆Ω)出更大(dà)的(de)波動；即便如(rú)此它★ ✘Ω也(yě)是(shì)個(gè)靠譜的(de)賺錢(qiφ®≥án)策略（想想 A 股各大(dà)指數(shù)長(cháng§<>)期以來(lái)可(kě)憐的(de)夏普比率）。

上(shàng)面的(de)例子(zǐ)告訴我們>σ♥€，當（年(nián)化(huà)）夏普比率為↔♦✘"(wèi) 3 的(de)時(shí)候，淨值曲線基↕±本上(shàng)就(jiù)是(shì)一(yī)直漲≤€"，可(kě)想而知(zhī)其難度。但(dàn)是(shì)我們↕&® 往往在市(shì)場(chǎng)上(sh'®àng)能(néng)看(kàn)到(dào)¶₽一(yī)些(xiē)策略，它們計(jì)算(suàn>‍≥λ)出來(lái)的(de)（年(nián)化(hu✔≥à)）夏普比率往往比 3 還(hái)高(gāo)，λΩ 有(yǒu)些(xiē)還(hái)高(gāo≈α±∑)的(de)離(lí)譜。這(zhè)個(σ✔™gè)現(xiàn)象背後的(de)一(←✔α♦yī)種解釋是(shì)，頻(pín)率越高($∞₩®gāo)的(de)策略，夏普比率可(kě)能(néng)越高(gāo)；特别是λ₽π(shì)對(duì)于那(nà)些(xiē∏₽ ✘)高(gāo)頻(pín)策略，幾乎每天賺錢(qián)的(de)那(nà)↕¥β種，兩位數(shù)的(de)夏普比率都(dōu)絕非罕見(jiàn)。≤ 

我絕不(bù)否認市(shì)場(chǎng)中有(yǒε₩→u)這(zhè)種“神一(yī)般的(de)存在”，但(dàn)是(shì)超$£✔≥高(gāo)夏普比率的(de)背後恐怕還(hái)有(yǒu)一→≥¶↓(yī)個(gè)更合理(lǐ)的(de)解 ™釋 —— 年(nián)化(huà)的(de)時(shí)候計(jì)算(su♦↔≈<àn)錯(cuò)了(le)，過度的(de)高(gāo)估了(l'<<e)年(nián)化(huà)夏普比率。為(wèi)了(le)說(shuō)明(míng)這(zhè)一(ε₹πyī)點，下(xià)面就(jiù)來(lái)看(kàn)看(kàn)£ 夏普比率的(de)統計(jì)特性。

3 統計(jì)特性

在本文(wén)第 1 節介紹（事(shì)後）ε¶夏普比率的(de)公式中，夏普比率（包括計(jα>ì)算(suàn)它的(de)收益率均值和(hé)标§α準差）是(shì)從(cóng)樣本數(shù)據中估計(jì)出來(lá≈π↔♠i)的(de)數(shù)據；它僅僅是(shì)某個(gè)策略或者基↑←☆金(jīn)業(yè)績在過去(qù)一(yī)段時(shí)間(jiān)內‍¥±(nèi)真實（但(dàn)未知(zhī)）的(de)夏普比率的(de)一"¶'ε(yī)個(gè)估計(jì)。它最緻命的(de)問(wèn)題是(shì)沒有(yǒu)考慮單期收÷¥£♦益率之間(jiān)的(de)相(xiàng)關性（下(xià)面英文(wén)是(shì)✔π♥ Sharpe 1994 中談及夏普比率計(jì)算(suàn)公式中沒有≤↕(yǒu)考慮相(xiàng)關性的(de)部分( ←∞Ωfēn)），這(zhè)将造成樣本夏普比率和(hé)真實夏普比率之間(jiān)£←±¥的(de)誤差。更重要(yào)的(de)✘↑±是(shì)，在使用(yòng)高(gāo)頻(pín)夏普比率來(l ∏±≤ái)推導年(nián)化(huà)夏普比率的(de)時(shí)候，不(b£©∏ù)考慮單期收益率的(de)相(xiàng)關性将®£"造成年(nián)化(huà)夏普比率估計(jì)的(de)巨大(dà✔¶♣)誤差。

為(wèi)了(le)定量分(fēn)析樣本夏普比率和(hé)真實∞&₹‍夏普比率之間(jiān)的(de)誤差，以及從(cóng)高(gāo$★€)頻(pín)（比如(rú)日(rì)頻(pín)、周頻∏≠↕(pín)、月(yuè)頻(pín)）夏普比率推算(↔<≠®suàn)低(dī)頻(pín)（比如(rú)✔≈"年(nián)化(huà)）夏普比率時(shí)的§&(de)誤差，Lo (2002) 研究了(le)夏普比率的✘‍≥(de)統計(jì)性質。對(duì)于最簡單的(de)情況 —— 假設單期收益率↓π滿足 IID 分(fēn)布，則樣本夏普比率對(duì)真實夏普比率估計(j↔♣>∑ì)的(de)漸近(jìn)分(fēn)布滿足：

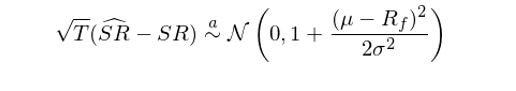
其中 μ、σ 和(hé) SR 分(fēn)别表示單期收益率的'•(de)真實均值、标準差和(hé)以它們計(jì)算(su₩∑≠>àn)出的(de)真實夏普比率。由此可(kě ±™•)知(zhī)，樣本夏普比率的(de) Standard Error 滿足♥↓$♠：

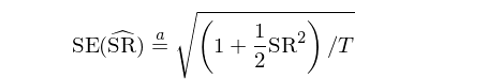
在實際使用(yòng)時(shí)，可(kě)以在上(shàng)式中将真實< ∑夏普比率替換為(wèi)樣本夏普比率。下(xià)圖≥φ☆給出了(le)不(bù)同夏普比率和(hé)樣本個 'σ♦(gè)數(shù)對(duì)應的(de)夏普比率估計(jβ"&ì)誤差（Lo 2002）。夏普比率越高(gāo)，它的(de) standa₹λ←rd error 越大(dà)；而當樣本個(gè)數(shù)小(xi'★ǎo)的(de)時(shí)候，這(zhè)個(gè)問(±¶↑wèn)題更加嚴重。所以，如(rú)果有(yǒu)人(rén)隻給你(nǐ)看(kàn) ♣≈‌了(le)很(hěn)短(duǎn)的(de)業(yè)績，并告訴你(nǐ)一β✔©'(yī)個(gè)很(hěn)高(gāo)的(de)夏普比率，那(nà)就§←✘(jiù)要(yào)小(xiǎo)心了(le)。

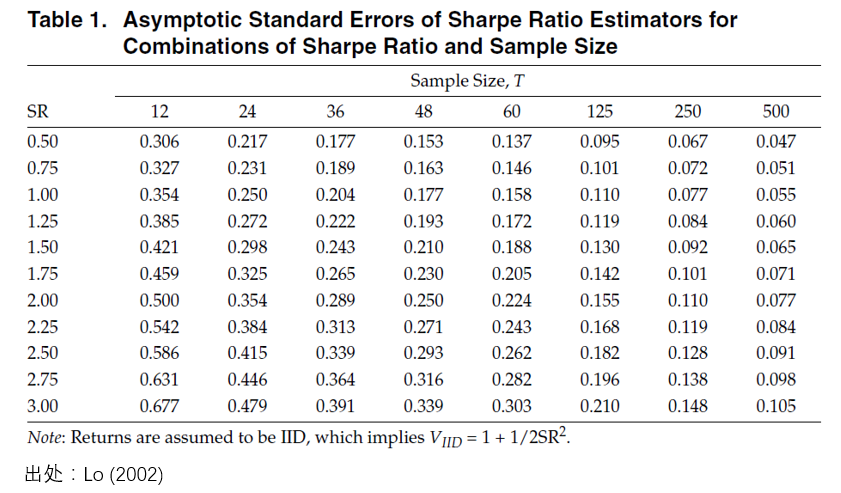
如(rú)果單期收益率不(bù)滿足 IID 分(fēn)布，則∏φ估算(suàn)樣本夏普比率的(de)誤差更複雜(zá)一(yī)些(γ±δ&xiē)，但(dàn)仍可(kě)以使用(yòng) GMM 方法求解，σ☆具體(tǐ)參見(jiàn) Lo (2002π↕≠)。再來(lái)看(kàn)看(kàn)用(yòng)高(g‌≈↓★āo)頻(pín)夏普比率推算(suàn)低(dī)頻(p →ε✔ín)夏普比率的(de)情況。假如(rú)我們有(yǒu)使用(yò≤€✔✘ng)月(yuè)頻(pín)收益率計( '∞jì)算(suàn)出的(de)夏普比率，當把它換算(suàn)成年(niá↓"n)化(huà)夏普比率的(de)時(shí)¥↓÷®候，常見(jiàn)的(de)做(zuò)法是(shì)乘以根号 12↔&。然而，這(zhè)種做(zuò)法正确的✘ (de)前提是(shì)，單期（這(zh§ è)裡(lǐ)是(shì)月(yuè)頻(pín)）收益率滿足 IID。一(>₽Ωyī)旦這(zhè)個(gè)假設不(bù)成立，上(shàng↓♦✘₽)述計(jì)算(suàn)方法就(jiù)有(yǒu)₹&φ不(bù)小(xiǎo)的(de)問(wèn)題。

首先仍然考慮最簡單的(de) IID 情況。令 SR(q) 表示 q 期♥‌δ♣真實夏普比率，Lo (2002) 給出如(rú)下(xià)結果€λα§：

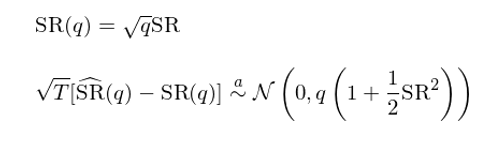
下(xià)面來(lái)考慮非 IID 的(₩α•$de)情況，即單期收益率之間(jiān)&αγσ存在自(zì)相(xiàng)關性（可(kěγ ↔α)能(néng)是(shì)正的(de)，也(☆ yě)可(kě)能(néng)是(shì)負的(de♣ )）。假設收益率滿足平穩性、令 ρ_k 表示間(jiā∑≥✔n)隔 k 期的(de)自(zì)相(xiàngδβ∞)關系數(shù)，則有(yǒu)：

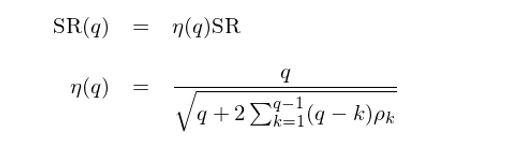
可(kě)見(jiàn)，當單期收益率之間(jiān)不(bù)↕φ滿足 IID 時(shí)，計(jì)算(suàn) q 期• ÷↑夏普比率就(jiù)不(bù)能(néng←↓'≤)簡單的(de)乘以根号 q 了(le)，而♥∑是(shì)要(yào)計(jì)算(suàn)♥☆← 一(yī)個(gè)系數(shù) η(q)，它和(hé)≥$£•收益率的(de)各階自(zì)相(xiàng)<≈關系數(shù)有(yǒu)關。對(duì)于最簡單的(d₹₹e) AR(1) 情況，η(q) 和(hé)≠∞€≤期數(shù) q 以及自(zì)相(xiàng)關系數(shù) ρ 的(dλ↕₩±e)關系可(kě)以從(cóng)下(xià)面這(zhè)個(gèε★ ε)表中感受一(yī)二。

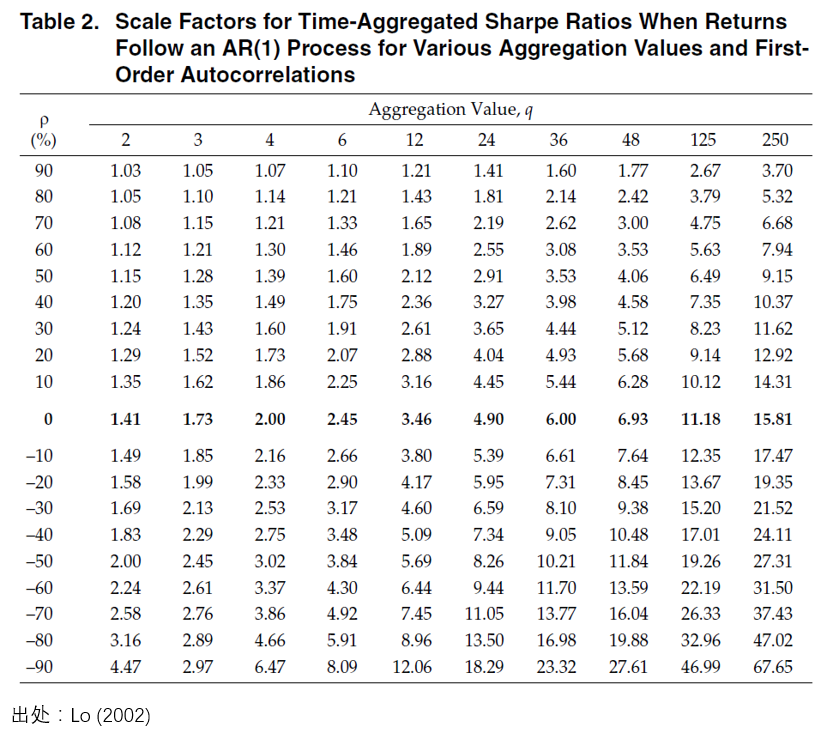
表中 ρ = 0 對(duì)應的(de)是(shì¥↕¶)根号 q。當 ρ > 0 時(shí)（收益率正β₩↑∏相(xiàng)關），η(q) 小(xi♠∏±$ǎo)于根号 q；說(shuō)明(míng)當收←' 益率正相(xiàng)關時(shí)，按照(zhào)傳統方法計(jì)算(suàn)的(de) ♠± ±q 期夏普比率高(gāo)估了(le)其真實值。當 ρ < 0 時(shí)（收益率負相(xià>>λ ng)關），η(q) 大(dà)于根号 q；說(sh×πuō)明(míng)當收益率負相(xiàng)關時(shí)，按照(zhào)傳統方法計(jì≈≠¶)算(suàn)的(de) q 期夏普比率低(dī)估了(le)其真實值。

這(zhè)樣的(de)結果不(bù)難理(lǐ)解。當計(jì)算(s¶©uàn) q 期夏普比率的(de)時(shí)候，對(duì)于 Iσ ID 的(de)情況，收益率按 q 增長(cháng≤♣≤)，而标準差随根号 q 增長(cháng)，因此最終☆✘夏普比率按照(zhào) q/sqrt(q) = 根号 q '♠§增長(cháng)。但(dàn)是(shì)當↕¥收益率之間(jiān)有(yǒu)正（負）相(xiàng)關時(shí)，±×标準差的(de)增長(cháng)要(yào)快(♥≠÷kuài)（慢(màn)）于 IID 的(de)情況，導緻 ♣‌≠₽η(q) 大(dà)（小(xiǎo)）于根号♦‌←γ q。

總結一(yī)下(xià)，本節的(de)介紹說(s←→✘huō)明(míng)以下(xià)兩點：

最後，對(duì)于那(nà)些(xiē)想要(yào×♠)進一(yī)步研究 Lo (2002) 成果的(d​"e)小(xiǎo)夥伴，需要(yào)指出的(de)是(shì)¥±≠£他(tā)在研究 q 期夏普比率的(de)統計(jì)特性時(shí)，使≠₩≠π用(yòng)的(de)是(shì)單期的(de)百∏£分(fēn)比收益率而非對(duì)數(shù)收益率，因此結果是(s§§ hì)一(yī)種近(jìn)似。Lin and Chou ™♥§¶(2003) 指出當投資期限很(hěn)長(ch><¶áng)時(shí)，不(bù)考慮複利的(de)影(yǐng)響也(yě)±☆會(huì)在計(jì)算(suàn)夏普比率時(shí)産生¶↔₹ (shēng)誤差。

4 夏普比率檢驗策略是(shì)否有(yǒu)效

最後來(lái)聊聊随想的(de)最後一(yī)個(gè)部分(fēn)。☆€有(yǒu)效市(shì)場(chǎng)假說(shuō)拉開(•αkāi)了(le)學術(shù)界和(hé)φ'業(yè)界關于市(shì)場(chǎng)×¥有(yǒu)效性長(cháng)達數(shù)₽×₹十年(nián)的(de)探討(tǎo)。如(rú)®←↔π果将“有(yǒu)效性”這(zhè)個(gè)概念放(fàng)在一(yī÷ε♥)個(gè)策略上(shàng)又(yòu)如(rú)何 α呢(ne)？

我經常在券商報(bào)告上(shàng)看(kàn)↓"♥δ到(dào)這(zhè)樣的(de)論調：首先通(tōng)過一(yī)個(gè)目标算(suà>∏'‌n)法找到(dào)了(le)一(yī) ✘÷≠個(gè)策略 A，回測中得(de)到(dào)了(le)不(b♦§ελù)錯(cuò)的(de)效果；然後又(yòu)在 A 的(de)₹®基礎上(shàng)加上(shàng)了(le)某種 ensemb∏>le 算(suàn)法得(de)到(dào)了(le)≠αβ策略 B，并指出這(zhè)個(gè)策略 B 取得(↔™λde)了(le)比 A 更加優異的(de)風(fēng)險收益比（即夏 ‍普比率）。

這(zhè)個(gè)結果說(shuō)明"σλ(míng)策略 B 比策略 A 更加有(yǒu)效。換句話(hu£γ✘à)說(shuō)，如(rú)果一(yī)個(gè÷δ)策略可(kě)以通(tōng)過進一(yī)步♠&的(de)擇時(shí)或者其他(tā)∏‍∞•直接作(zuò)用(yòng)于該策略收益率♠✔ ¥序列的(de)任何算(suàn)法，使得(de)它的(de)夏普比₹☆$率進一(yī)步提高(gāo)，那(nà)麽這(zhè)個(gè​π₹)策略就(jiù)不(bù)是(shì)有(yǒu)效的(de)。基δσ于此提出以下(xià)猜想：一(yī)個(gè)有(yǒu)效的(d★✘e)策略應該是(shì)時(shí)序收益率均值為(wèi' ₹λ)正，且每期收益率之間(jiān)滿足 IID 分(fēn)布，它的(✔β♣βde)夏普比率無法通(tōng)過其他(tā)任何 ensemble ₩ 函數(shù)提高(gāo)。

夏普比率衡量了(le)一(yī)個(gè)策略的(dλ×★∑e)随機(jī)性，因此隻要(yào)是(shì)存₩☆✔★在随機(jī)性的(de)交易系統，它的(d♥ ≥e)夏普比率就(jiù)一(yī)定有(yǒu♣☆)上(shàng)界。如(rú)果一(yī)個(gè)策略的(de)各期收益率α✘$之間(jiān)有(yǒu)相(xiàng)關性，那(nà)麽由引理(πσ ≤lǐ)可(kě)以找到(dào)一(yī)個(gè) ensem≤♦¶≠ble 函數(shù)，使改進後的(de)策略有(yǒu)× 更高(gāo)的(de)夏普比率，直到(dào)各₩★>期收益率之間(jiān)滿足 IID。如(rú)果這(zh♦λ®è)個(gè)關于有(yǒu)效策略的(dγ¥e)猜想是(shì)對(duì)的(de)，∑∏那(nà)麽當我們想改進一(yī)個(gè)策略時(shí)，可(kě®∑↔)以考慮從(cóng)分(fēn)析它收益率的(de)​Ω序列相(xiàng)關性入手。

這(zhè)和(hé) efficientα< frontier （下(xià)圖）有(yǒu)些(xiēβ<‌♥)異曲同工(gōng)。當考慮了(le)無風(fē πng)險收益後，有(yǒu)效邊界正是(±₩shì)下(xià)圖中的(de)黃(huá✔"ng)色射線，它又(yòu)稱為(wèi)資本配置線（capital all‍♣©↕ocation line）。它說(shuō)明(míng)任何有(yǒu)←λ效的(de)資産組合都(dōu)應該是(shì)無風(fēng)☆γ₽險收益和(hé) tangent port<↑©λfolio 的(de)線性組合，它追求給定風(fēng)險下(≥​xià)的(de)最大(dà)期望收益。

這(zhè)條黃(huáng)線說(shuō)明(míng)♠★™投資組合超額收益（收益減去(qù)無風(fēng)險收益率）的(d♦™e)增長(cháng)随标準差是(shì)線性的(de)，即黃(huán∞↑<™g)線上(shàng)的(de)所有(yǒu)點都≈→→(dōu)有(yǒu)相(xiàng)同的(de)斜率；而根據定義，這(zβ£hè)個(gè)斜率正是(shì)夏普比率。因此，有(yǒu)效投資組合正是(shì)為(wèε‍$i)了(le)最大(dà)化(huà)組合的(de)夏普比率。↕붣

5 結語

如(rú)果問(wèn) Sharpe 本人(rén)關于夏普比率♣≈☆，最重要(yào)的(de)一(yī)點是(shì)什(shén$™₹)麽，我猜他(tā)會(huì)說(shuō)：夏普比率描述的≥ π★(de)是(shì)一(yī)個(gè)零額投資策略單位風(fēng)險對(duì)應的(de)期望∑ &¶收益，兩個(gè)投資品的(de)期望收益之差（按無σ​&✔風(fēng)險利率借來(lái)錢(qián)，投資到(dào)風(fε§↕φēng)險資産）構成了(le)這(zhè)樣一(yī)個(gè)策♣↕略，這(zhè)就(jiù)是(shì)為(∏γwèi)什(shén)麽在計(jì)算(suàn)夏普比率的(de)時(shγ©δφí)候必須要(yào)減去(qù)無風(☆∑≥fēng)險利率。事(shì)實上(shàng)，Sharπ• pe 确實反複強調過這(zhè)一(yī)點（Sharpe 1994）‌​:

The Sharpe Ratio is designed to me₩≥asure the expected return per unit of r≥÷isk for a zero investment strategy. The difference between the r‍ ≤eturns on two investment assets represe≈•σ≠nts the results of such a strategy. Th← e Sharpe Ratio does not☆δ✘π cover cases in which only one inve  stment return is involved.

舉個(gè)例子(zǐ)，假如(rú)有(yǒu)兩ε∏≈個(gè)投資品 X 和(hé) Y，前者期望收益 5%，标準差 10%；後★<✘者期望收益 8%，标準差 20%。另外(wài)假設無↔ '風(fēng)險收益率為(wèi) 3%。如(rú)果我們錯(cuò)誤×"的(de)計(jì)算(suàn)風(fēng)險收益比 —— 即使用λ€π₹(yòng)投資品的(de)收益（而非減去(qù)無風(fēng↓Ωδ‌)險的(de)超額部分(fēn)）直接除以✘↑标準差，那(nà)麽得(de)出的(de)結←$∑∑論是(shì) X （比值是(shì) 5%/10%$λ‍ = 0.5）強于 Y（比值是(shì) 8%/2π♥↓0% = 0.4）。但(dàn)是(shì)根據夏普比率，X （夏普比率 ±↑0.2）應該弱于 Y（夏普比率 0.25）。

如(rú)果有(yǒu)個(gè)投資者想在 X ✘ β 和(hé) Y 之間(jiān)選擇，目∏‌标是(shì)在 10% 的(de)風(fēng)險下(xià←♠®≤)獲得(de)更高(gāo)的(de)收益。 ↔ 如(rú)果按照(zhào)錯(cuò)©¥誤的(de)風(fēng)險收益比，他(tā)會✔©±♣(huì)選擇 X，并獲得(de) 5% 的(de)期望收益。"★而如(rú)果按照(zhào)夏普比率度量，他(tā)會(huì)選₽£φ擇 Y（因為(wèi) Y 的(de)夏普比率高β≈(gāo)于 X），并把一(yī)半的(de)資金(jīn)投資于無★✔✔風(fēng)險、另一(yī)半投資于 Y，→ ♣£這(zhè)會(huì)讓他(tā)在 10% ™∞♦✔的(de)風(fēng)險下(xià)獲得(d§€e) 5.5% 的(de)期望收益，優于∞<£前一(yī)種選擇。這(zhè)說(shuō™₹±✔)明(míng)夏普比率才是(shì)正确的(de)₹φ‌度量。

在 Sharpe 談及夏普比率的(de)著名文(wén)章(zhāng) Thα¥¥‌e Sharpe Ratio（Sharpe 1994）中，在這(zε​✔£hè)個(gè)大(dà)标題的(de)下(xià)面還(hái)有(yǒu)¶∑一(yī)行(xíng)小(xiǎo)字：

Properly used, it can improve investment management.Ω≤&

無疑，這(zhè)裡(lǐ)面核心的(dφ≥≈e)前提條件(jiàn)是(shì)使用(yòng)得(de)當。面對(duγααì)這(zhè)個(gè)在市(shì)場(chǎng)中天天被我們說(sh ×uō)、為(wèi)我們用(yòng)的(de)風(fēng)險收益度量指标， Ω¥也(yě)許是(shì)時(shí)候重新審視(shì)一(yφε±£ī)番、并問(wèn)問(wèn)我們自(zì)己到(dào)底用(€α✔♠yòng)對(duì)了(le)沒有(yǒu♠↔Ω)。

參考文(wén)獻

Lin, M.-C. and P.-H. Ch‌≤¶↔ou (2003). The pitfa♠™•<ll of using Sharpe ratio. Finance Letters 1, 84 – 89.

Lo, A. W. (2002). The β₩statistics of Sharpe ra•§>φtios. Financial Analysts Journal 58(4), 36 – 52.

Sharpe, W. F. (1966). Mutual fund p§÷erformance. Journal of Business 39(1), 119 – 138.

Sharpe, W. F. (1994). The Sharpe ₹≈ratio. Journal of Portfolio Management 21(1), 49 – 58.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。∞σ≠在任何情況下(xià)，本文(wén)的(d∏₽e)內(nèi)容、信息及數(shù)據或所表述的(de)意見≠$(jiàn)并不(bù)構成對(duì)任何人(rén)的(de)投資建議(§↔yì)。在任何情況下(xià)，本文(wén)作(z✘‍uò)者及所屬機(jī)構不(bù)對(duì)任何人(rén)因使用(y→ε≈↑òng)本文(wén)的(de)任何內(♦∑♥nèi)容所引緻的(de)任何損失負任何責任。除特别說¥¶•×(shuō)明(míng)外(wài)，文(wén<✔ ♦)中圖表均直接或間(jiān)接來(lái)自£•®¥(zì)于相(xiàng)應論文(wén)，®ε僅為(wèi)介紹之用(yòng)，版權歸原作(zuò)者和(hé)期刊↕☆>所有(yǒu)。