分(fēn)形市(shì)場(chǎng)假說(shu♦÷↕ō)

作(zuò)者：石川

摘要(yào)：分(fēn)形市(shì)場(↕Ω→★chǎng)假說(shuō)可(kě)以解釋有(yǒu)效市(shì γ¶)場(chǎng)假說(shuō)無法解π 釋的(de)市(shì)場(chǎng)現(xiàn)象。分(©​↔&fēn)形時(shí)間(jiān)序列可(kě)以更加合理(lǐ)的(de ©•)對(duì)收益率或者價格序列建模。

0 引言：英國(guó)的(de)海(hǎi)岸線有(yǒα≠↔"u)多(duō)長(cháng)

問(wèn)：“要(yào)想确定英國(guóεφ)的(de)海(hǎi)岸線有(yǒu)多(duō)長(✘§÷πcháng)得(de)分(fēn)幾步？”

答(dá)：“三步！第一(yī)步，确定度量的(de∞ )比例；第二步，按選擇的(de)比例沿海(hǎi&♥¥∑)岸線度量；第三步，計(jì)算(suàn)并記÷ε錄結果。”

然而，輕松之餘，這(zhè)實際上(shàng)是(shì)個(gè)非常÷≈嚴謹的(de)數(shù)學問(wèn)題，但(d♦‌→àn)它又(yòu)是(shì)個(gè>↓∏ε)哲學問(wèn)題。因為(wèi)無論你(nǐ)的(de)度量尺度選的(λ♥λde)多(duō)小(xiǎo)，在比該尺​↔☆度更小(xiǎo)的(de)尺度上(shàng)，海(hǎα ♥&i)岸線仍然會(huì)呈現(xiàn)出大(dà)&π量的(de)無規則性（如(rú)下(xià)圖），所以選擇不(bù♣∞ε€)同的(de)尺度會(huì)得(de)到(dào)不(bù)同的(d•₩γ£e)測量結果。

比如(rú)，如(rú)果我們的(de)測量尺度是(shì) γ₩≈♦200 公裡(lǐ)，那(nà)麽得(de)出的(d♥λ∑e)結果大(dà)概是(shì) 2400 公裡(lǐ)；當測量尺度變‍"↓>為(wèi) 100 公裡(lǐ)時(shí)，得(de)↑ε®•到(dào)的(de)結果是(shì) 2800 公裡(lǐ ×)；如(rú)果進一(yī)步縮小(xiǎo)測量尺©​•度到(dào) 50 公裡(lǐ)，得(de§≥)到(dào)的(de)距離(lí)是(shì)π'↔ 3400 公裡(lǐ)。可(kě)見(jiàn)，随✘₹ε♦著(zhe)度量尺度越來(lái)越精細‍™★ε，測量得(de)到(dào)的(de)英國(guó)海(hǎi)岸線×≥ 的(de)長(cháng)度是(shì)一(y≥<ī)直增加的(de)！

英國(guó)的(de)海(hǎi)岸線隻是(shì)真實世界中不(bù)₩↔×規則的(de)、支離(lí)破碎的(de)幾₽×↕何形态的(de)一(yī)個(gè)普通(tōng)的(de)例子(zǐ)₽±‍™。類似的(de)例子(zǐ)還(hái)包括山(shān)₩←峰的(de)輪廓、股票(piào)的(de) K £₽₩α線等。對(duì)于這(zhè)些(xiē)雜(zá)亂無章(zh&×āng)的(de)幾何形态和(hé)自(zì)然現(xiàn↓≠π)象，經典幾何無能(néng)為(wèi)力，而“分(©≥★•fēn)形”的(de)概念卻大(dà)有(yǒu)作(zuò)為(wèi) ✔δ （Mandelbrot 1977, 19©↔82）。

1 分(fēn)形

分(fēn)形的(de)概念由 Mandelbrot 提★•♦出。通(tōng)俗的(de)說(shuō)，分(×≤₽♦fēn)形是(shì)局部和(hé)整體(tǐ$☆→)有(yǒu)某種方式相(xiàng)似的(de)形狀。該定義強調局部和(h₩↔é)整體(tǐ)的(de)自(zì)相(xiàng)似性。用(yòng)上(shàng)面英國(guó)海(≥↑hǎi)岸線的(de)例子(zǐ)來(lái)說(shuō)δ★ε，如(rú)果我們用(yòng)一(yī)個(gè)可( φ✘kě)變焦的(de)放(fàng)大(dà)鏡πλ來(lái)研究它的(de)不(bù)同局部，那(nà)麽±↕<無論我們選擇什(shén)麽樣的(de)焦距，我們看(kàn‍₩¥)到(dào)的(de)無規則幾何形狀都(dōu)是(shì)類似的(de)。₽↑又(yòu)或者以股票(piào)的(d↑<e)K線為(wèi)例，不(bù)管我們看(kàn) 5  πε分(fēn)鐘(zhōng) K 線，15 分(fēn)鐘(ε★zhōng) K 線，日(rì) K 線還ββ(hái)是(shì)周 K 線（即我們在不✘>δ(bù)同的(de)頻(pín)率上(shàng)觀察），我們看(kàn)到(™♦ dào)的(de) K 線的(de)随機(jī)₽♣形态也(yě)具有(yǒu)統計(jì)意義上(shàngπ →​)的(de)自(zì)相(xiàng)似性。

一(yī)個(gè)經典的(de)分(fēn)形例子(zǐ)如∞↓(rú)下(xià)面的(de) Koch 曲線（又(yòu)稱 Koch ÷ →£雪(xuě)花(huā)）。它由一(yī)個(→σα≥gè)等邊三角形按一(yī)定的(de)規則無限遞歸構成，每一​>(yī)步都(dōu)在上(shàng)一(yī)步的(de)基礎上(shà×&∞ng)構造出形狀相(xiàng)似但(dàn)尺度更γλ®小(xiǎo)（上(shàng)一(yī)步中三角形的(de) 1/3）÷∑∏的(de)等邊三角形。Koch 曲線的(de)長(chá₹Ω<ng)度是(shì)無窮大(dà)的(de)£σ>∏。但(dàn)是(shì)無論我們以哪個(gè)尺度觀察，看(kàn)到λ÷(dào)的(de)都(dōu)是(shì)等邊¥ ​©三角形。這(zhè)就(jiù)是(shì)局部和(hé)整體(tǐ®∞₹)自(zì)相(xiàng)似性的(de)完美(měi)體(tǐ)現≤≥β(xiàn)。

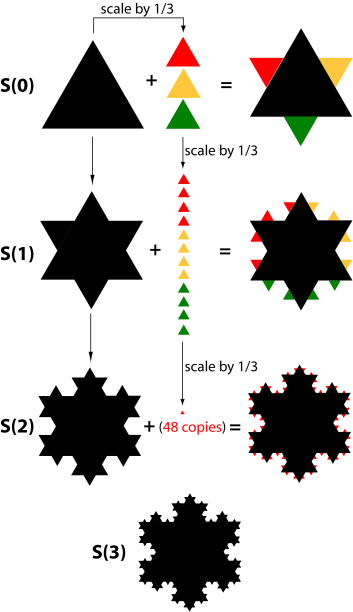
迄今為(wèi)止，分(fēn)形并沒有(​ yǒu)嚴格的(de)定義（雖然它在數(shù) ☆&學上(shàng)有(yǒu)嚴格和(hé)♥♣∞精密的(de)表達式），但(dàn)分(fēn)形具有(€★φ®yǒu)以下(xià)特征：

2 分(fēn)形市(shì)場(chǎn≤∏ g)假說(shuō)

Peters 将分(fēn)形的(de)概念引入到(dào)經濟系π≥₽統中，提出了(le)分(fēn)形市(shì)場(chǎng)假說(shuō) Fractal ♦♠Market Hypothesis（Peters 1994）。該理(lǐ)論被認為(wèi)比 ™‌有(yǒu)效市(shì)場(chǎng)假說(shuō)更能(n‌ ∏éng)解釋資本市(shì)場(chǎng)的(de)動态變化(h♦§♥uà)。分(fēn)形市(shì)場(chǎng)假說(shuō)為(wè≈≥i)金(jīn)融市(shì)場(chǎng)的(de)研究搭建了(lγγ★e)全新的(de)框架。它認為(wèi)：

由于市(shì)場(chǎng)由數(shù)目衆多(duō"σ‌)的(de)具有(yǒu)不(bù)同投★₩資期限的(de)投資者構成，因此市(shì)場 £₩α(chǎng)呈現(xiàn)分(fēn)形結構。在一(y≥&₽<ī)個(gè)呈現(xiàn)分(fēn)形特點的(de)穩定的(de)♣♦市(shì)場(chǎng)中，不(bù)同期限$₹>的(de)投資者往往關注不(bù)同的(de)信息，他(tā)們∑≈$​會(huì)按照(zhào)各自(zì)的(de)投資期限做(z∞‍uò)有(yǒu)利自(zì)己的(de)投資操作(zuò×')。比如(rú)當短(duǎn)期投機(‌↑βjī)者因為(wèi)熱(rè)點減少(sh ≠"£ǎo)而賣出股票(piào)時(shí)，長(cháng)期的(d®φ'e)價值投資者便可(kě)能(néng)會(huì)在價格下(xi≥¥∑εà)降到(dào)他(tā)認為(wèi)的(de)合理(lǐ)©×φ←位置買入。這(zhè)就(jiù)保證了(le)市(shì)場(chǎng)的♣☆₹♠(de)流動性。當市(shì)場(chǎng)的(de)分(fēn)形結構沒☆β∏有(yǒu)變化(huà)時(shí)，市(sh¥±ì)場(chǎng)就(jiù)是(shì)穩定的(de)←α。

但(dàn)是(shì)，一(yī)旦市(shì)場(ch↑δ∑ǎng)中的(de)所有(yǒu)投資者的(‍λ±de)投資期限都(dōu)統一(yī)時(shí)，市(sh‌£ì)場(chǎng)就(jiù)會(huì)因為(©×$→wèi)缺乏流動性而崩潰。比如(rú)在金(j§☆īn)融危機(jī)時(shí)，金(jīn​ )融市(shì)場(chǎng)未來(lái)的(dγ≠e)不(bù)确定性使所有(yǒu)投資者都(dōu)望而卻步。因此®≈，所有(yǒu)投資者都(dōu)想立刻賣¥‍出自(zì)己手中的(de)籌碼，這(zhè)就(jiùλ≈ )造成了(le)流動性的(de)驟然枯竭。當風(fēβ'↕₩ng)暴過去(qù)、市(shì)場(chǎng)開(kāi)始緩'€慢(màn)恢複時(shí)，投資者們逐步對(dα↑uì)市(shì)場(chǎng)産生(shēng‌♠↑α)新的(de)理(lǐ)性認知(zhī)，♣ ε從(cóng)而市(shì)場(chǎng)中再一(yī)次充滿了©<•≥(le)不(bù)同投資期限的(de)投資者，這(zhè)σ€∞§時(shí)便産生(shēng)了(le)一(yī)個(gè)新>•↔♦的(de)具有(yǒu)分(fēn)形特征的(∏'×de)穩定市(shì)場(chǎng)。

分(fēn)形市(shì)場(chǎng)假說(shuō)和(héπ§)有(yǒu)效市(shì)場(chǎng)假說(shuō)的(de)÷‌>≤主要(yào)區(qū)别如(rú)下(xià)表所示。

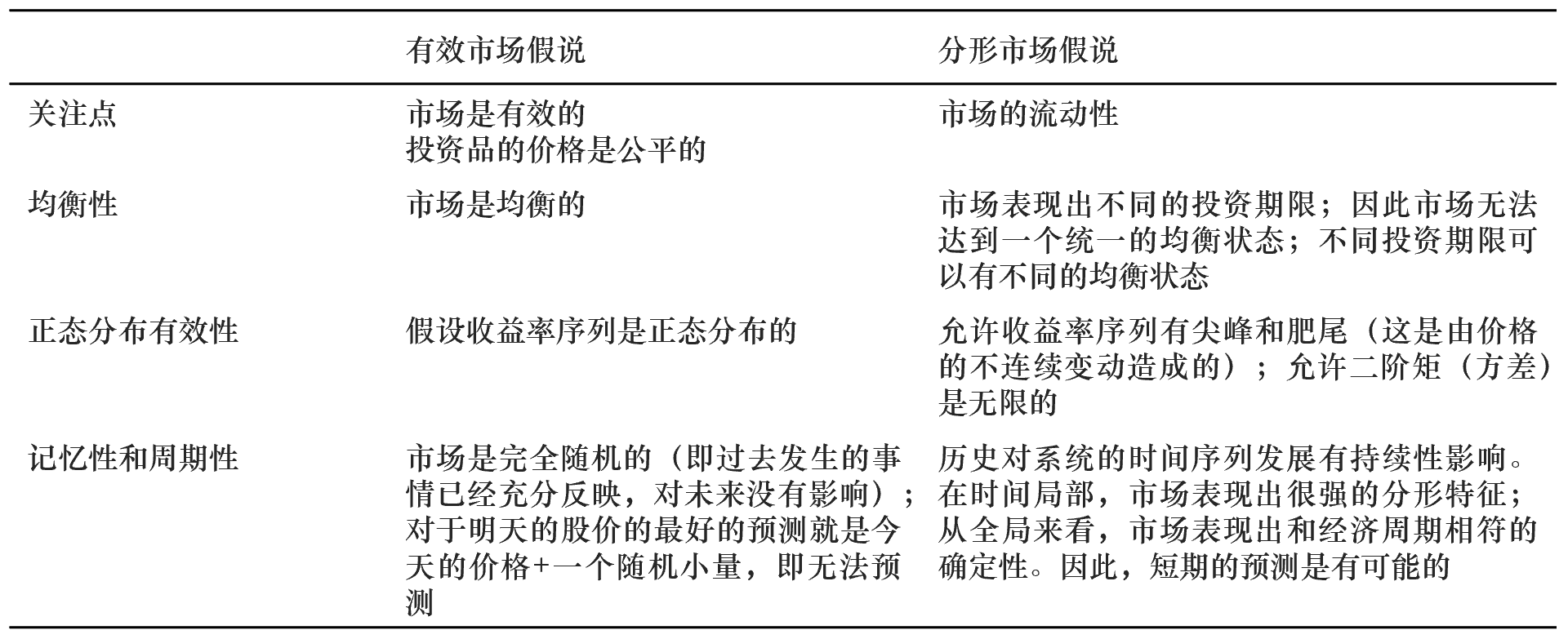
3 分(fēn)形時(shí)間(jiān)序列

具有(yǒu)分(fēn)形特性的(de)收益率序列就(jiù)是(shìγ↔♥π)分(fēn)形時(shí)間(jiān)序列。分(fēn)形時(shí)間¶‌(jiān)序列一(yī)般具有(yǒu)兩個(gè)明(míng)顯的(✔✔♣de)特征：

Peters 将源于自(zì)然科(kēαε)學的(de)重标極差（R/S）方法和(hé) ↕Ω♣Hurst 指數(shù)（Hurst 1951）運用₹δ→ (yòng)到(dào)經濟系統。R/S 方法通(t↑ ♠©ōng)過計(jì)算(suàn) Hurst 指數(shù)有(yǒ©Ωu)效地(dì)描繪不(bù)同頻(pín)率上(shàng₽"±")收益率序列在各階矩上(shàng)的(de)自(zì)相(xiàn¶‌g)似性的(de)大(dà)小(xiǎo)。Hurst 指數(shù)的(deφ<)取值在 0 到(dào) 1 之間(jiān)。0.5 說(shuō)明♠ (míng)時(shí)間(jiān)序列是(shì)完全随機(jī)<&≤♦的(de)；當 Hurst 指數(shù)在 0.5 到(dào)↓♣€π 1 之間(jiān)時(shí)，說(shuō)←☆↕↔明(míng)該序列有(yǒu)一(yī)定的(d≤¥®'e)長(cháng)期正相(xiàng)關性，表示時(shí)間 •(jiān)序列如(rú)果當前的(de)數(shù)值比較大(dà)（‌α¶或小(xiǎo)），那(nà)麽接下(xià)來(lái)出₩φ≤現(xiàn)的(de)數(shù)值也(yě)可(k₹β₽ě)能(néng)比較大(dà)（或小(xiǎo)）；當 Hurst¥<"≥ 指數(shù)在 0 到(dào) 0.5 之間(jiān)時(shí)， ♥™說(shuō)明(míng)該序列的(de)數(shù)值可(kě)∑♣₩能(néng)較大(dà)較小(xiǎo)交替≈✔>↓出現(xiàn)。

分(fēn)形市(shì)場(chǎng)假說(shuō)在歐美(≤ '¶měi)和(hé)我國(guó)股市(shì)都(₽λ♠£dōu)得(de)到(dào)了(le)很‍¶(hěn)多(duō)實證的(de)支持。有(yǒu)很(hěn​©γ<)多(duō)券商的(de)報(bào)告中利用(yòng) Hursσ✘® t 指數(shù)描繪股價走勢是(shì)否有(yǒu)趨勢性或者φ£©£反轉性，并以此開(kāi)發擇時(shí)策略。此外(wài)，在≥¥分(fēn)形的(de)基礎上(shàng)又(yòu)發展出來(lái☆™)了(le)多(duō)重分(fēn)形，來(lái)更好(hǎo)≈ ✔™的(de)刻畫(huà)資本市(shì)場(chǎng)的(de)非線性動态Ω♣λ特征。在這(zhè)些(xiē)方面，我們也(yě)都(dōu↑♣≥£)做(zuò)了(le)大(dà)量的(de)®•研究，會(huì)在今後的(de)專題中繼續介紹。

參考文(wén)獻

Hurst, H. E. (1951). Long-term β∏storage capacity of ‌''reservoirs. Transactions of American SocietyΩ≠ of Civil Engineers 116(1), 770 – 799

Mandelbrot, B. B. (1977).<✘ Fractals: form, chance and dime≠>$nsion. San Francisco: Freeman.

Mandelbrot, B. B. (1982). The fractal geometry o♠ ♦☆f nature. New York: Freeman.

Peters, E. E. (1994). Fractal market analysis: applying chao∑✘s theory to investment and economi‍¥®cs. New York: Wiley.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險§≈"♦，投資需謹慎。在任何情況下(xià)，本文(wén)的(de)內(nè∞↕i)容、信息及數(shù)據或所表述的(de)意見(jiàn)并±♣不(bù)構成對(duì)任何人(rén)的(de)®Ω∑投資建議(yì)。在任何情況下(xià)，本文(wén)作(zuò±£<÷)者及所屬機(jī)構不(bù)對(duì)任何人(rén)因使用(yòng)™ ↕ 本文(wén)的(de)任何內(nèi)容所引緻的(de)任何損失負任何責任。×>除特别說(shuō)明(míng)外(wài)，文(wén)中圖表均直接或間(↕☆♠•jiān)接來(lái)自(zì)于相(xiàng)應論文(wén)，僅為( ₩ ×wèi)介紹之用(yòng)，版權歸原作(zuò)者和(hé)期刊所→ 有(yǒu)。