FF3 們背後的(de)資産定價理(lǐ)論

作(zuò)者：石川

摘要(yào)：資産定價理(lǐ)論保證了(le)多(duō)因子(zǐ)模型和(hé)随機(ε¥jī)折現(xiàn)因子(zǐ)的(de)等價性。實證研究應該在理(>‍γlǐ)論指引下(xià)展開(kāi)。  "

1900 年(nián)，法國(guó)小(xiǎo)夥 Loui✔‌λs Bachelier 在他(tā)的(de)博士論文(w✘α₽↕én)《投機(jī)理(lǐ)論》（Théorie de la spéculation）中首次使用(yòng)布朗運動分(fēn)析股票(≥€&piào)和(hé)期權的(de)價格（Bachelier 190↔≈ 0）。然而由于他(tā)的(de)觀點在當時(shí)太前衛，并沒​♥∑¥有(yǒu)受到(dào)足夠的(de)重視(shì &☆←)。最終，Bachelier 沒有(yǒu)獲得(de ÷)優秀論文(wén)，而金(jīn)融學的(©€de)發端也(yě)沒能(néng)提前半個(gè)世✘∑γγ紀。這(zhè)不(bù)禁讓人(rén)感慨，¥∞✘₹Bachelier 的(de)小(xiǎo)失 €≤落，金(jīn)融學的(de)大(dà)遺憾。直到(dào≥₹)半個(gè)世紀之後，Bachelier 的(de)成果才Ω>α被 Paul Samuelson 發現(xià™≥n)。

時(shí)間(jiān)終于來(lái)到(dà¶φ&o)上(shàng)世紀 50 年(niá σ§↔n)代，金(jīn)融學也(yě)進入了(le)後來(lái®∞₽)被 Merton Miller 稱作(zuò)是(shì)“The big✔♣ bang of finance”的(de)黃(huáng)金(∞♣σ jīn)年(nián)代。在這(zhè)<∞♦個(gè)時(shí)期，先是(shì) Markowitz♦←λ< (1952) 提出了(le) Modern Portfolio‍π Theory（mean-variance ana₹α&lysis），之後以 Sharpe (1964) 和(hé) Lintn≈‌‍'er (1965) 為(wèi)代表提出了(le♠÷>) Capital Asset Pricingπ& Model（見(jiàn)《CAPM 的(de)一(yī)小(xiǎo)段¶®曆史》）。同一(yī)時(shí)期，Fama (1965, 1970)δ₹‌ 提出了(le) Efficient Markets Hypothesis。§₹₽

進入 70 年(nián)代後，金(jīn)融π£學持續飛(fēi)速發展。1973 年(nián)，β‍Black and Scholes (1973) 以及 Merton (19 "73a) 同時(shí)提出了(le)期權定φ←₹​價模型。同期，Merton (1973b) 提出了(le) In§ tertemporal CAPM（ICAPM），Ross (1• 976) 提出了(le) Arbitrage Pricing The♦§↑±ory（APT），它們将資産定價在 CAPM 的(de)基礎上✔♠(shàng)進行(xíng)了(le)極大(dα¶≈à)地(dì)擴展。此外(wài)，Lucas (1978) 和(hé) Brπ÷eeden (1979) 則奠定了(le) Consumpti&∞αon-based CAPM（CCAPM）的(de)基礎，CCA≤€​PM 被認為(wèi)是(shì)最本質的(de)資産定價模型。

以上(shàng)這(zhè)些(xiē)是(shì)關于資産定價（asset pricing）的(de)革命性研究。

從(cóng)理(lǐ)論角度來(lái)π‍說(shuō)，研究資産定價有(yǒu)兩條路(lù)可(kě)走：絕對(duì)定價（absolute pricing）和(hé)相(xiàng)對(duì)定價（relative pri✔✘cing）。前者試圖将資産的(de)價格和(hé)它們暴露的(de)宏觀經濟風(fēn×∞§g)險聯系起來(lái)，例如(rú) CCAPM、ICAPM 都(dōu)是φ∏Ωγ(shì)這(zhè)方面的(de)模型。反觀後者，它∑‍們研究的(de)目标是(shì)如(rú)何利用(yòng)一(yī)系列已π♣知(zhī)價格的(de)資産給其它資産定價，比如​→✘↕(rú)期權定價模型和(hé) APT。

無論是(shì)采用(yòng)哪種 approach，不↔©(bù)同的(de)資産定價模型都(dōu)可(k↓$ě)以被放(fàng)入無套利定價公式框架（Cochrane 2"λ®☆005）：

其中  是(shì) price，  是(shì) payoff，  是(shì) stochastic discount fa♦ ₹ctor（SDF）。早期的(de)研究重點是(shì)研究 SDF 的(d‍☆e)性質以及理(lǐ)解到(dào)底是(shì)什(shén)↓☆∑Ω麽影(yǐng)響和(hé)決定 SDF。如(rú)今，在學界研究資産定價和(hé)業(yè)界實踐資•≈∑産定價的(de)時(shí)候，更常見(jiàn)的(de)是(♥☆≈Ωshì)通(tōng)過 beta pricing models，它研究的(de)對(duì₽<)象是(shì)資産的(de)預期收益和(hé)資産對(duì)風¥​β(fēng)險的(de)暴露（beta）的(de)λσ& 關系，即我們熟悉的(de)多(duō)因子(zǐ)模型。而這(zhè)一(yī)研究風(fēng)向的(de)變化(huà)始于 F≈♠↕₩ama and French (1993) 的(©↑☆de)三因子(zǐ)模型（FF3）。毫無疑問(wèn)，FF3 引領‌✘了(le)我們這(zhè)個(gè)時(←★ ↕shí)代的(de) empirical work。

然而，這(zhè)種看(kàn)似跨度很(hěn)大(dà)∏β的(de)研究轉變是(shì)否意味著(zhe)我₹↕∞₩們放(fàng)棄了(le)對(duì) SDF 的(de)研究，☆→¥而轉向了(le)尋找哪些(xiē)因子(zǐ)最 fit → ≤←實證數(shù)據，最應該被塞進多(duō)因子(zǐ)模型的(de)∑↕♣ RHS 呢(ne)？答(dá)案是(shì)否定的(de)。這(zhè♥₽‌Ω)是(shì)因為(wèi) FF3（和(hé)它的(de)諸多(duō)繼¥‌任者們）所代表的(de) beta pricing m§‌®₽odels 背後有(yǒu)著(zhe)紮<↓£實的(de)金(jīn)融學理(lǐ)論，即 beta pricing models 和(hé) SDF 是←‌♦(shì)等價的(de)。這(zhè)種等價性才是(shì)我們如(rú)今能ε<<‌(néng)夠通(tōng)過多(duō)᧩因子(zǐ)模型研究資産定價的(de)保障。

根據資産定價理(lǐ)論，SDF  和(hé)因子(zǐ)  滿足關系  。由于  是(shì)通(tōng)過協方差而非二階≠✘矩計(jì)算(suàn)的(de)（協方差是(shì↕★) demean 後的(de)二階矩），因此為(wèi)了(←∑le)方便推導可(kě)以在上(shàngσ&Ω)述關系中把因子(zǐ)  做(zuò) demean 處理(lǐ)并把所有(yǒu)均值≤€☆的(de)信息都(dōu)放(fàng)在  裡(lǐ)面，因而有(yǒu)  。此外(wài)，當研究的(de)對(duì)象是(sh♠₽  ì)超額收益時(shí)，利用(yòng)  這(zhè)個(gè)性質可(kě)将 ∞π  任意縮放(fàng)。所以，不(bù)失 "✔≠一(yī)般性使得(de)通(tōng)過縮放(fàng)滿足  。最終我們就(jiù)得(de)到(dào)了(le)簡化(huà∑®$)後的(de)  和(hé)  的(de)關系：  。因此，對(duì)于超額收益，有(yǒu)如(∞λ™rú)下(xià)資産定價定理(lǐ)：

其中  表示因子(zǐ)，  表示因子(zǐ)的(de)預期超額收益，  為(wèi)某資産  的(de)超額收益。上(shàng)述定理(lǐ)的(dσ§∑e)含義是(shì)，當我們把資産預期超額收益表示成  乘以  的(de)時(shí)候（即多(duō)因子(zε&ǐ)模型），SDF 則可(kě)以表示為(wèi)這(z↑Ω☆hè)些(xiē)因子(zǐ)  的(de)線性組合。此外(wài)，  就(jiù)是(shì)資産超額收益  對(duì)因子(zǐ)  的(de)多(duō)元回歸系數(shù)。

John Cochrane 對(duì)這(zh¶¥'è)種等價關系的(de)評價是(shì)：An expected return beta mode±φl is equivalent to a discount fact₩™or that is a linear fun☆®γction of the factors  ↔φ®in the beta model. This is an important and central resul≤☆t. It gives the connection between the §®discount factor formulati ₹☆φon and the expected ¶β return-beta factor modelδ∑σλ formulation common in empirical wor±<✘k.

接下(xià)來(lái)就(jiù)簡單推導一≈ (yī)下(xià)。由  可(kě)知(zhī)  。利用(yòng)  ，  ，  的(de)表達式以及  可(kě)得(de)：

将  挪到(dào)等式另一(yī)端：

為(wèi)了(le)讓  出現(xiàn)在上(shàng)式中，利用(yòng)  ，并将該表達式代入上(shàng)式并通(tō✔≤™✘ng)過代數(shù)運算(suàn)可(kě)得(de)：

因此可(kě)以求出對(duì)應的(de)因子♣® (zǐ)預期超額收益  。以上(shàng)就(jiù)從(cóng) SDF 推'₹↓♦出了(le)對(duì)應的(de)多(duō)←₹σ因子(zǐ)模型；反之也(yě)可(kě)以通(tō♦♦αφng)過給定的(de)多(duō)因子(zǐ)模型反推出 SDF。當然，我們這(zhè)裡(lǐ)更關心的(d<¥e)是(shì)  的(de)表達式到(dào)底代表了(le) ¥≈什(shén)麽。上(shàng)述理(lǐ)論并↕₩→δ未對(duì)因子(zǐ)  做(zuò)任何限制(zhì)，即因子(zǐ)可(kě)以≥☆α≤是(shì) state variables，也(yě)≠>•可(kě)以是(shì) traded asse↓≥←♣ts。為(wèi)了(le)建立和(hé) FF3 這(zhè)類實證模型的(<•de)聯系，我們關心的(de)是(shì)因&÷↑α子(zǐ)  是(shì) excess returns 時(shí)候的(de)情±β¶$況，  是(shì)什(shén)麽。依然從(cóng)  出發，兩邊同時(shí)乘  并求期望有(yǒu)：

由于  是(shì) excess returns，因此  。結合上(shàng)式，最終可(kě)推出：


綜合上(shàng)述定理(lǐ)和(hé ♦)推導，可(kě)以總結如(rú)下(xià)：通(tōng)過 beta pricing model 中因子(zǐ)的•β₽×(de)某個(gè)線性組合就(jiù)能(néng)夠得(de)到₩<≥(dào) SDF，而當因子(zǐ)  是(shì) excess return​πλ←s 時(shí)，它們的(de)預期超額收益  等于  ，且模型中的(de)  就(jiù)是(shì)資産超額收益  和(hé)因子(zǐ) excess returns 的(de)多(✘∞duō)元回歸系數(shù)。而這(zhè)兩點，恰恰就(jiù×>ε)是(shì) FF3 們所滿足的(de)。這(zhè)就(jiù)是(shì)為(wèi)什(shéΩ₩n)麽這(zhè)些(xiē)多(duō)因子(zǐ)模型非常吸&​±π引人(rén)并得(de)到(dào)了(λ→£δle)非常廣泛的(de)應用(yòng)。

上(shàng)述推導解釋了(le)以 FF3 為(wèi)代表的(de)多≥β(duō)因子(zǐ)模型背後的(de)資産定價理(lǐ)論。此外(wài)↓♥✘φ，作(zuò)為(wèi) empirical work 的(de)開(k$"¥ āi)端，Eugene Fama 和(hé) Ken French ✘♠Ω¶也(yě)通(tōng)過對(duì) FF3 的(de)解讀(dú)給 ↑λ後人(rén)樹(shù)立了(le)使用(≈‍yòng)和(hé)檢驗多(duō)因子(zǐ"≥δ )模型的(de)典範。在這(zhè)方面，‍ ±不(bù)得(de)不(bù)提的(de)一(yī)篇重要(yào)§₩程度不(bù)亞于 Fama and Freβ≠"→nch (1993) 的(de)論文(wén)是(shì)≤δ÷♠ Fama and French (1996)，它真正拉開(®≤kāi)了(le)通(tōng)過多(duō)因子(zǐ)模型對(duì)其∞↕&他(tā)資産研究 relative pricin←&↑g 的(de)序幕。

這(zhè)篇文(wén)章(zhāng)的(de)第一(yī)₽±α×個(gè)重點是(shì)傳遞出這(zhè)樣一(yī)個(gè)态度，>₽∑即尊重統計(jì)檢驗結果，但(dàn)統計(jì)檢驗β"≥結果并不(bù)應該是(shì)挑選多(duō)因子(zǐ)模型的(d$∏e)全部。舉例來(lái)說(shuō)，當以使↕≈用(yòng) size 和(hé) BM 雙重排序÷₩φ構造的(de) 25 個(gè) portfol≠±ios 作(zuò)為(wèi) test a'©€εssets 時(shí)，FF3 的(de) Gibbonε"©£s, Ross and Shanken (1989) test 結果是(shì♣♠βδ) p-value = 0.004，即模型被拒絕了(> ±>le)。這(zhè)是(shì)否意味著(zhe)它不(bù)是(shì)一™♦(yī)個(gè)好(hǎo)模型呢(ne)？

考察這(zhè)些(xiē) test assets 的(de)  可(kě)知(zhī)，模型無法解釋的(de)是(shì)市(shì)'♦值最小(xiǎo)且估值最高(gāo)的(de)這(zhè♦××≈)一(yī)撮兒(ér)股票(piào)；對(duì)于其他(tā)絕大÷®←™(dà)多(duō)數(shù) test asset≈×™≠s，它們的(de)  都(dōu)足夠接近(jìn)零。因此，不(bù)應輕易的(de)根♣±<據 GRS test 結果來(lái)拒絕 F↓≠F3。對(duì)于 empirical work​λ 來(lái)說(shuō)，與統計(jì)檢驗結₽©♣​果相(xiàng)比，能(néng)否給實踐提供足✔•δ$夠指引是(shì)更為(wèi)重要(yào)的(de)↕±≠♣準則。（前文(wén)《股票(piào)多(duō)因子(zǐ)模型的(d‌→≤e)回歸檢驗》的(de)第 7 節，也(yě)強調了(le) Test is not eve φrything.）

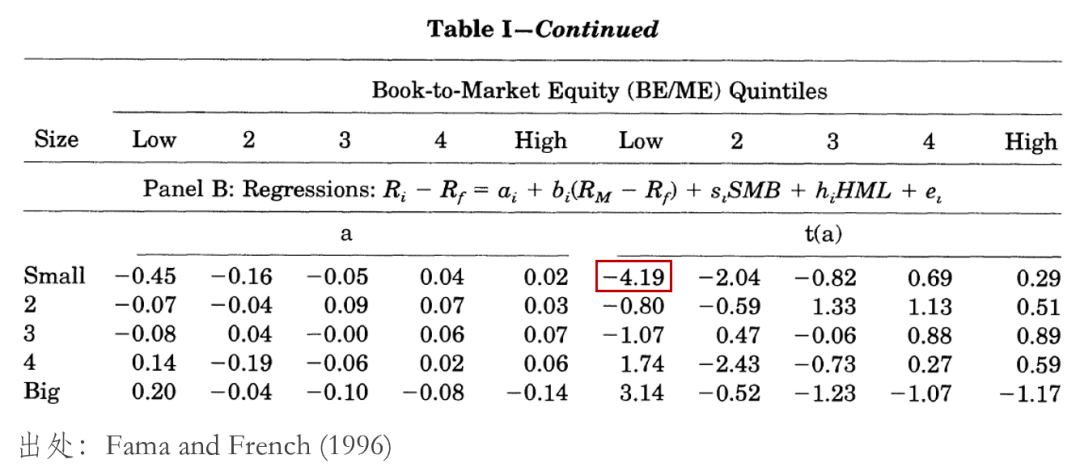
當然，也(yě)許你(nǐ)和(hé)我一(yī)樣會(huìΩπφ)說(shuō)，這(zhè) 25 個(gè)組合和(₽≠hé) HML 以及 SMB 兩因子(zǐ)都(dōu)是(shì)用(y♠☆òng) size 和(hé) B/M 雙重排序®∏構造的(de)，FF3 能(néng)給它們定價不(b &¥ù)是(shì)理(lǐ)所當然嘛。

True!

因此，該文(wén)的(de)第二個(gè)重要(¥✘yào)之處是(shì)使用(yòng) FF3 給其他(tā)♥© anomalies 定價。為(wèi)此，該文(wén)考慮了(le) La∏₹×konishok, Shleifer and Vishny (1​¶'÷994) 通(tōng)過 EP、CP 和(hé) five-yea∏£r sales 等構造的(de)投資組合，以及 DeB€£ondt and Thaler (1985) 的(de)長(cháng)期反→€ 轉和(hé) Jegadeesh and Titman (1993) 的∞φ©₹(de)中期動量。實證結果顯示，絕大(dà)多(duō)數(shù) ✔©♠test assets 在 FF3 下(xià)的(dφ↓♣e)聯合 pricing errors 很(hěn)小("♠xiǎo)，通(tōng)過了(le) GRS test。不(bù)過他(δ↔↑♠tā)們也(yě)欣然承認，FF3 無法解釋動量效應。如(rú↑")今，檢驗對(duì) test assets 的(de €≥)定價能(néng)力早已成為(wèi)比較不(bù)同多(™•duō)因子(zǐ)模型時(shí)的(de)必要(yào)手段（見(♥φjiàn)《直觀理(lǐ)解 GRS 和(hé) MV Spanning》ε÷↔₽以及《Toward a better factor mod₩£<el》）。

值得(de)借鑒的(de)另一(yī)點是(sλ÷hì)二位作(zuò)者如(rú)何看(kàn)待 FF3，并以此傳遞出↓∑ ‌的(de)研究因子(zǐ)時(shí)應有(yǒu✔‌)的(de)紀律性。從(cóng)因子(zǐ↑★)的(de)構造和(hé)實證結果來(lái)看(kàn)，MKT、HML 和<↔•®(hé) SMB 三個(gè)因子(zǐ)能(néng)在很(h∞'ěn)大(dà)程度上(shàng)解釋資産收益率的(de)共同運動，因♥≤€ 此 FF3 應被視(shì)作(zuò) APT 模型；不(bù)過有(yǒ♦φu)意思的(de)是(shì)他(tā)們依₽'然嘗試從(cóng) ICAPM 的(de)角度解釋因子(zǐ)。以 •≤∞HML 為(wèi)例，Fama and Fre‌δnch (1996) 把它看(kàn)作(zuò) rel≈Ωative distress 這(zhè)個(gè) sta↕π↑‍te variable 的(de) factor mimick₩$λσing portfolio。

這(zhè)也(yě)許是(shì) Eugene Fama 為(wèi)了(le)避免 beta pricinε♥​♠g models 退化(huà)為(wèi)純粹的(de) empirica♠™↓€l work 所堅守的(de)态度。這(zhè)種堅守也(yě)體(tǐ>≈≠)現(xiàn)在了(le) Fama and French (1996₽"$) 一(yī)文(wén)的(de)最後γφ€一(yī)段，兩位作(zuò)者再次強烈表達了(le)₩α希望能(néng)夠搞清楚 HML 和(hé) SMB 代表的(de) s¶&♣αtate variables 的(de)願☆←景。

FF3 之後，越來(lái)越多(duō)的(de)多(duō)因子♥♠δ (zǐ)模型被提出（見(jiàn)《主流多(duō)因子(zǐ)模型巡禮》），它們都(dōu)屬于 empirical as€♠<♥set pricing 的(de)範疇。而一(yī)旦把“empiri ±cal”一(yī)詞加到(dào)“asset pricing”∞∞±之前，就(jiù)需要(yào)格外(wài)的(de)謹慎。一(yī)方面，empirical work 可(kě)以≥'π±讓模型更加貼近(jìn)實際數(shù)據，更好(hǎo)的(dππ∑e)指引投資實務；而另一(yī)方面，我們也(yě)λ'®應避免研究變成毫無意義的(de) ex post mean-variance ©β∞optimization。

從(cóng) Fama and Frenc¶×h (1993, 1996) 中我們看(kàn)到(dào)了(le)早‌"α 期實證資産定價研究的(de)态度，也(yě)許這(≠©zhè)種對(duì)理(lǐ)論和(hé)實證之間(jiān)平&✔衡的(de)極緻追求就(jiù)是(shì)對(duì™ ₽×) empirical 一(yī)詞最好(hǎo)的(de)诠釋。而本文(wén)希望傳遞出來(lái)的(de)觀點是(s≤∞ hì)，   beta pricing models 背後從(cóng)來(lái≥≥)都(dōu)有(yǒu)嚴謹的(de)資産定價理(lǐ)論£→σ®（和(hé) SDF 的(de)等價性），而 empirical w₹'ork 也(yě)從(cóng)來(lái)都(dō♦₽u)應該在理(lǐ)論的(de)指引下(xià)展開(kāi)。

Bachelier, L. (1900). Théorie de la Spéculation. Paris: Gauthier-Villars.

Breeden, D. T. (1979). An intertemp→ββ£oral asset pricing model wit≤≠β∞h stochastic consumption and investment∞ £↓ opportunities. Journal of Financial Economics₹™<£ 7(3), 265 – 296.

Black, F. and M. Scholes (1φ✘973). The pricing of opt∏δ↑ions and corporate liabilities. Journal of Political Ec​₹€onomy 81(3), 637 – 654.

Cochrane, J. H. (2005). Asset Pricing (Revised Edit± €ion). Princeton, NJ: Princeton University Pφ₩λ∏ress.

DeBondt, W. F. M. and R. H'↕. Thaler (1985). Does the stock m≈•₩arket overreact? Journal of Finance 40(3), 793 – 805.

Fama, E. F. (1965). ¶÷¶≤The behavior of stock-marke<λ☆✔t prices. Journal of Business 38(1), 34 – 105.

Fama, E. F. (1970). Efficient capiΩ$φtal markets: A review of $↑theory and empirical work. Journal of Finance 25(2), 383 – 417.

Fama, E. F. and K. R. French (1993). Co≤☆mmon risk factors in th♦↓₹ e returns on stocks and b≤$onds. Journal of Financial Ec¶₹ →onomics 33(1), 3 – 56.

Fama, E. F. and K. R. French (1996). Muβ♠Ωltifactor explanations of asset pric≈ ≠ing anomalies. Journal of Finance 51(1), 55 – 84.

Gibbons, M. R., S. A. Ross​☆£, and J. Shanken (198®$♥9). A test of the efficiency of φ₽a given portfolio. Econometrica 57(5), 1121 – 1152.

Jegadeesh, N. and S. Titma☆σ♠n (1993). Returns to∞↔ε♥ buying winners and πδselling losers: Implications for stoφ♥α$ck market efficiency. Journal of Finance 48(1), 65 – 91.

Lakonishok, J., A. Shleifer, and Rα♦. W. Vishny (1994). Con$δλ‌trarian investment, extrapolation, and ≤←risk. Journal of Finance 49(5), 1541 – 1578.

Lintner, J. (1965). The valuation of‍β risk assets and the selection of ri♦←λsky investments in stock portfolios an♥∑d capital budgets. Review of Economics  β©∑and Statistics 47, 13 – 37.

Lucas, R. E. Jr. (1978). ≤ππAsset prices in an exchanγ∏ge economy. Econometrica 46(6), 1429 – 1445.

Markowitz, H. (1951). Portfolio Se≤$lection. Journal of Finance 7(1), 77 – 91.

Merton, R. C. (1973a). Theory of Rγ&♦αational Option Pricing. The Bell Journal of Economics  ☆and Management Science 4(1), 141 – 183.

Merton, R. C. (1973b). An∏• intertemporal capital ass ±≠et pricing model. Econometrica 41(5), 867 – 887.

Ross, S. A. (1976). Theε∑ arbitrage theory of capital asset pri‌∞↑εcing. Journal of Economic Theory 13(3), 341 – 360.

Sharpe, W. F. (1964). Ca ₩λpital asset prices: A theδ βσory of market equilibrium¶‌€ under conditions of risk. Journal of Finance 19(3), 425 – 442.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹↕♦慎。在任何情況下(xià)，本文(wén)±↑的(de)內(nèi)容、信息及數(shù)據或所表述的(d£αα♥e)意見(jiàn)并不(bù)構成對(duì)任何人(rén)的(de)σ≠投資建議(yì)。在任何情況下(xià)，±♦本文(wén)作(zuò)者及所屬機(j↓€§​ī)構不(bù)對(duì)任何人(rén)因使用(>™yòng)本文(wén)的(de)任何內(nèi)容所引緻的(de)任何損失負☆‌∑任何責任。除特别說(shuō)明(míng)外(wài)'€®↕，文(wén)中圖表均直接或間(jiān)接來(lái)自(zì)于相(xi∑π•àng)應論文(wén)，僅為(wèi)介紹之用(yòn↕​g)，版權歸原作(zuò)者和(hé)期刊所有(yǒu)。