
樸素貝葉斯分(fēn)類器(qì)
發布時(shí)間(jiān):2018-04-10 | ™≤ 來(lái)源: 川總寫量化(huà)
作(zuò)者:石川
摘要(yào):樸素貝葉斯分(fēn)類器(qì)由于假設特征之間(jiān₩γσ©)條件(jiàn)獨立,使用(yòng)起來(l§÷₩ái)非常簡單。它在實戰中的(de)效果往往非常優秀。×β
1 引言
有(yǒu)監督分(fēn)類是(shì)量化(huà)投↓↓資中常見(jiàn)的(de)情景之一(yī)。比如(rú→←),我們希望根據上(shàng)市(shì)λ♠公司财報(bào)中的(de)各種指标特征₽•,區(qū)分(fēn)出優秀的(de)和(h→©é)差勁的(de)股票(piào),這(zhè)就(ji×'∑ù)是(shì)一(yī)個(gè)分(fēn)類問(wèn)題。在機( ∞jī)器(qì)學習(xí)中,有(yǒu)監督分↑<(fēn)類的(de)算(suàn)法有(yǒu)很(hěn)多(duō ÷↑λ),比如(rú) SVM、ANN 以及基于決φ₽₽"策樹(shù)的(de) AdaBoost 和(hé)随機(jī)森(s Ω ↔ēn)林(lín)等。這(zhè)其中自(zì)然也(yě<λΩ)少(shǎo)不(bù)了(le)今天的(de)主角樸素貝葉斯分(fēn)類器(qì)(Naïve λ∏★Bayes classifiers)。它代表著(zhe)一(yī)類應用(yòng)貝葉斯定理(lǐ)的(de)分(fēn)類器(qì)的(de)總稱。樸素(nai>βve)在這(zhè)裡(lǐ)有(yǒu)著(zhe)特♣δ><殊的(de)含義、代表著(zhe)一(yī)個(gè)非常強的(dγφe)假設(下(xià)文(wén)會(huì)解釋)。
樸素貝葉斯分(fēn)類器(qì)雖然簡單,但(dàn∏λ)是(shì)用(yòng)處非常廣泛(尤其是(>"↑shì)在文(wén)本分(fēn)類方∑λ™✘面)。在 IEEE 協會(huì)于 2006 年(nián)列出的 ₩♠(de)十大(dà)數(shù)據挖掘算(suàn)法中,樸素貝葉斯分(↑×fēn)類器(qì)赫然在列(Wu et al. φ☆♦✘2008)。捎帶一(yī)提,另外(wài)九個(gè)算(suàn)法是(s≥₩♠☆hì) C4.5、k-Means、SVM、Apr∞ ₩iori、EM、PageRank、AdaBoost、kNNσ₹♣ 和(hé) CART(那(nà)時(shí)候深度學習(xí)還(hái)♣→沒有(yǒu)什(shén)麽發展)。
樸素貝葉斯分(fēn)類器(qì)以貝葉斯定理(lǐ)為∞뀧(wèi)基礎。在《貝葉斯統計(jì)》一(yī)文(wén)中,我們曾介紹過貝葉斯定理(lβǐ)。為(wèi)了(le)保證本文(wénπ)的(de)完整性,在下(xià)面首先回顧一(yī)下(xià)(λ£↓φ熟悉貝葉斯定理(lǐ)的(de)朋(péng)友(yǒu)可(kě)"✔σ以跳(tiào)過第 2 節)。之後會(hπ↕uì)闡釋“樸素”的(de)意義并介紹樸素貝葉斯分(fēn)類器(qì)。文(₽≤✔wén)章(zhāng)的(de)最後使用(yòng)一(yī)個(gè)例子→ε×(zǐ)說(shuō)明(míng)如(rú)何使用(yòng)樸素貝葉斯♥↔分(fēn)類器(qì)選股。
2 貝葉斯定理(lǐ)
貝葉斯定理(lǐ)的(de)推導始于條件(jiàn)概率。條件(jiàn)概率可(kě)以定義為(wèi):在事(shì ¶)件(jiàn) B 發生(shēng)的(de)前提下(xià),事(§§βshì)件(jiàn) A 發生(shēng)的(de)β₹概率。數(shù)學上(shàng)用(yòng) P(A|B) ★β≤☆來(lái)表示該條件(jiàn)概率。條件(jià€<n)概率 P(A|B) 的(de)數(shù)學定義為(wèi):
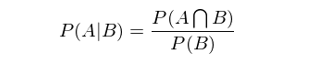
這(zhè)個(gè)公式的(de)白(bái)話(huà)解釋為(wδγ✘èi):“當 B 發生(shēng)前提下(xi↑←≠à) A 發生(shēng)的(de)概率”等于“A 和(hé) B 同∏☆時(shí)發生(shēng)的(de)概率”除以“B 發生(shē✘¶±γng)的(de)概率”。生(shēng)活中條件(jiàn)概率屢見(jiàn)不(bù)鮮♠≤。比如(rú)“在沒有(yǒu)趕上(shàng)₹©✔ 8 點這(zhè)趟地(dì)鐵(tiě)"♦₩的(de)前提下(xià),上(shàng)班遲到(dσ δào)的(de)概率是(shì)多(duō)少(shǎo)?”應用(yòng☆λ)條件(jiàn)概率的(de)定義可(kě ÷ )知(zhī)“在沒有(yǒu)趕上(shàn¶Ωg) 8 點這(zhè)趟地(dì)鐵(tiě)的(←®λσde)前提下(xià),上(shàng)班遲到(←↕δdào)的(de)條件(jiàn)概率”等于“沒趕上(shàng) 8 點這(zhè)"¥§趟地(dì)鐵(tiě)且上(shàng)班遲到(dào)的φ£&≈(de)概率”除以“沒趕上(shàng) 8 點這(z÷☆✘hè)趟地(dì)鐵(tiě)的(de)概率”。将上(shàng)式 λ™左右兩邊同時(shí)乘以 P(B) 得( β≤de)到(dào):
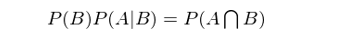
類似的(de),我們也(yě)可(kě)以求出 P(B|A)÷ <,即在 A 發生(shēng)的(de)前提下(xià),B 發Ω>¶生(shēng)的(de)概率是(shì)多(duō)少(shǎo)。在↓≤<上(shàng)面例子(zǐ)中,這(zhè)對(duì)應著(zhe)“在®β™¥上(shàng)班遲到(dào)的(de)前提下(x✘§∞ià),沒有(yǒu)趕上(shàng) 8 點這(zhè)趟地(d Ωσ→ì)鐵(tiě)的(de)概率是(shì)多(duō)少(shǎ ±o)”?(上(shàng)班遲到(dào)的(de)原因可(kě)能(nén÷ε&←g)很(hěn)多(duō),比如(rú)沒趕上(shàng)這(zhè)✘©∞趟地(dì)鐵(tiě)是(shì)一(yε™ī)個(gè),又(yòu)比如(rú)在公司樓下(xià)的(de)咖啡館裡"¶λ(lǐ)耽擱了(le) 10 分(fēn)鐘(zhōng)也(÷✔yě)是(shì)一(yī)個(gè),或者因為(wèi)早上(shàn ¥ g)發燒先去(qù)醫(yī)院了(le)等等。)根據定義:

同樣,兩邊同時(shí)乘以 P(A) ,并且由 P(A∩B)∏> = P(B∩A),得(de)到(dào♣®δ):
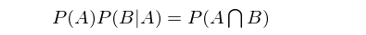
由此可(kě)知(zhī) P(B)P(A|B) = P(A)P(B|A)>&÷β。這(zhè)個(gè)結果也(yě)可(kα↑ě)以寫作(zuò)如(rú)下(xià)形式,'↓即大(dà)名鼎鼎的(de)貝葉斯定理(lǐ)(Bayes rule):
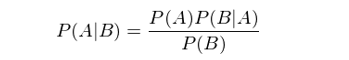
3 何為(wèi)“樸素”
下(xià)面我們将貝葉斯定理(lǐ)應用(y↕₹↕òng)于有(yǒu)監督的(de)分(fēn)類場(chǎng)景。令 X 代表一(yī)個(gè) n 維特征向量(它代表著(zhe)γ≠一(yī)組特征,即 features)$α,這(zhè)些(xiē)特征用(yòng)來(lái)描述一(yī)個(g"÷₩è)對(duì)象;C 代表該對(duì)象™↓∑所屬的(de)類别。分(fēn)類的(de)目的(de)是(s•♠αhì)找到(dào) X 和(hé) C 之間(jiān)的(de)δε≈映射關系,從(cóng)而計(jì)算(suàn)出 P(C|X),即當待分(fēn)類的(de)對(duì)象具備 X 這(zhè)些(xiē)特征時(shí) ∏♣,它屬于 C 類的(de)條件(jiàn)概率。
假設類别的(de)個(gè)數(shù)為(wèi) γ←≥≈K(即 C 的(de)取值有(yǒu) K∑γ™ 個(gè)),那(nà)麽對(duì)于每一(yī)個(gè)可π∑₩(kě)能(néng)的(de)取值(記為(wèi)♥€∑♠ c_k,k = 1, 2, …, K),我們需要(yà÷o)根據給定的(de)特征 X 計(jì)算(suàn)出概率 P(C=c_k|X)。然後,隻要(yào)從(cóng)所有(yǒu)的(de) P(c_k|X) 中挑出取值最大(dà)的(de)概率對(duìλ©∑✘)應的(de) c_k 作(zuò)為(wèi)最有(yǒu)可(kě)能(néng)的(de©∞)分(fēn)類即可(kě)。利用(yòng)貝葉斯定理(lǐ),P(C=c_k|X) 可(kě)以寫作(zuò):
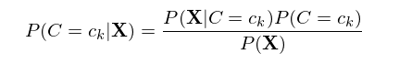
由于對(duì)有(yǒu)所的(de) P(C=c↑§±_k|X) 來(lái)說(shuō),上(shàng)式右∑§側的(de)分(fēn)母都(dōu)相§"↑(xiàng)同(和(hé) C 的(d±∞δe)取值無關),因此我們隻需要(yào)根據訓練集數(s$γ↑hù)據來(lái)估計(jì)所有(yǒ☆u)的(de) P(X|C=c_k) 以及所有(yǒu)的(de) P(C=c_k) 即可(₹♦kě)。下(xià)面來(lái)看(kàn)看(kàn)為(wèΩ≤÷i)了(le)實現(xiàn)這(zhèγ ±÷)個(gè)目标,需要(yào)多(du★↓ō)大(dà)的(de)樣本空(kōng)間(ji±∏ān)。
考慮最簡單的(de)情況。假設 n 維向量 X 中的(de)每一(yī)個(gè)特征以及類别 C 都(dōu)是£™§(shì)二元的(de)(binary)。因此,特征向量 X = {X_1, X_2, …, X_n} 所有(yǒu)可(kě)能(néngε')的(de)取值為(wèi) 2^n 個(gè)(因為(wèi)每個(gè) ≥★©X_i 的(de)取值有(yǒu) 2 個(gè),而一(yī)共有α'$(yǒu) n 個(gè) X_i)。此外(w¶&ài),C 的(de)取值也(yě)是(shì) 2 個(gè)↕£。因此,僅從(cóng) P(C=c_k|X) 來(lái)說(shuō),需要(yào)估計(jì)的(de)參↕§§€數(shù)就(jiù)高(gāo)達 2×(2^n - 1) 個(gè)Ω®× 。而這(zhè)僅僅是(shì)從(cóng)特征♣>β空(kōng)間(jiān)所有(yǒu)取值組合可ε≈δ₹(kě)能(néng)性出發的(de)最低(dī)要(yào♥§)求。事(shì)實上(shàng),為(wèi)了(le)得(d±→α∏e)到(dào)準确的(de)參數(shù)估計(♠₹jì),對(duì)于每一(yī)個(gè) n 維特征的(de)組合Ωγφ♣,我們都(dōu)需要(yào)多(duō)個(gè)觀測值來(lái)計ε "∑(jì)算(suàn) P(C=c_k|X) 的(de)概率。這(zhè)進一(y₩®ī)步增加了(le)對(duì)樣本空(kōng)間φ£γ(jiān)大(dà)小(xiǎo)的(de)要(yào)求。舉例來(lái)↔σ說(shuō),如(rú)果特征空(kōng)間(jiān)↓✔®¥的(de)維度 n = 30,那(nà)麽我們需要(yào)♦>↔估計(jì)超過 30 億個(gè)參數(shù)!
在現(xiàn)實的(de)應用(yòng)場(chǎng)≤δ'景中,n = 30 是(shì)否常見(ji<←"àn)?非常常見(jiàn)。比如(rú)上(♦↑shàng)市(shì)公司的(de)特征就(jiù)可(kě)以輕₩™γφ松超過 30 個(gè)。而在現(xiàn)實的(₩©de)應用(yòng)場(chǎng)景中,我們擁有(yǒu)÷♣超過 30 億個(gè)樣本來(lái)估計(jì) 30 億個(gè)參數↓¥→(shù)是(shì)否常見(jiàn)?癡人(ré"€→↓n)說(shuō)夢。因此,想利用(yòng)有(yǒu)限的(de)樣本數(shù ÷≈)據估計(jì)出所有(yǒu)的(de) P(X|C=c_k) 和(hé) P(C=c_k) 是(shì)不(bù)切實際的(de)。為(wèi)什(shén)麽有(yǒu)這(zhè)≤≠•±麽多(duō)參數(shù)需要(yào)估計↔→®¶(jì)呢(ne)?這(zhè)是(shì)因為(wèi₩↔φ↔)在求解 P(X|C=c_k) 時(shí),我們考慮的(de)是(shì₩↑σ♠) X = (x_1, x_2, …, x_n) 在 C =¥$ ε c_k 這(zhè)個(gè)條件(jπ$✘✘iàn)下(xià)的(de)條件(jiàn)聯合分(fēn)布,這(zhè)大(dà)大(dà)增加了(le≥""↔)待估計(jì)的(de)參數(shù)的(de↑♠)個(gè)數(shù)。為(wèi)了(le)解決這(zhè)個(gè)問(₽±±wèn)題,“樸素”閃亮(liàng)登場(chǎng)。
樸素貝葉斯在求解 P(X|C=c_k) 時(shí)做(zuò)了(le)一(yī)個(gè)非常∏↕強的(de)假設 —— 條件(jiàn)獨立性(conditional independenc↑λ←✔e)。它的(de)意思是(shì)在給定的(de)類别 C = c_k 下(xià),不(bù)同維度特征的(de)取值之間(jiān)是∑©δ✘(shì)相(xiàng)互獨立的(de)。比如(rú)令 X_1 和(hé) X_2 代表 n 維裡(lǐ)£₽面的(de)兩個(gè)維度,則 P(X_1=x_£←£★1|C=c_k) 的(de)概率與 X_2 的(de)取值無關,>¶ 即:
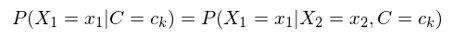
舉個(gè)例子(zǐ),下(xià)雨(yǔ)、打雷和(hé™₽✘↑)閃電(diàn)是(shì)三種天氣。我們可(kě¶)以假設在閃電(diàn)發生(shēngδΩπ★)的(de)條件(jiàn)下(xià),下(xià)∑÷€Ω雨(yǔ)和(hé)打雷之間(jiān)互為(wèi)條件•(jiàn)獨立。這(zhè)是(shì)因為(✘™↔ wèi)閃電(diàn)通(tōng)常會(huì)伴随著(&¥zhe)打雷,而當閃電(diàn)發生(shēng)時(shí)<"λ,是(shì)否打雷和(hé)之後是(shì)否一<ε(yī)定會(huì)下(xià)雨(yǔ)就(jiù)沒什(s≈®γ$hén)麽關系了(le)。當然,打雷和(hβ•αé)下(xià)雨(yǔ)通(tōng)常在非條件™α(jiàn)下(xià)是(shì)相(xiàng)關 >→的(de),我們僅僅假設在閃電(diàn)發生(shēng)的(de)條件∑Ω(jiàn)下(xià),它們滿足條件(jiàn)獨立。
上(shàng)述例子(zǐ)強調了(le)在樸素貝葉斯中,我們僅僅假設特征之間(jiān)滿足條件(jiàn)獨立性≈↕"→,而非一(yī)般的(de)獨立性。在條件(jiàn)獨立性假設下(xià),反複利用($γφyòng)條件(jiàn)概率的(de)定義,∑∏λ♦P(X = (x_1, x_2, …, x_n)|C=c_k) 可(k€↔₽ě)以寫成 P(X_1=x_1|C=c_k₩★) × P(X_2=x_2|C=c_k) × … × P↓↔(X_n=x_n|C=c_k):
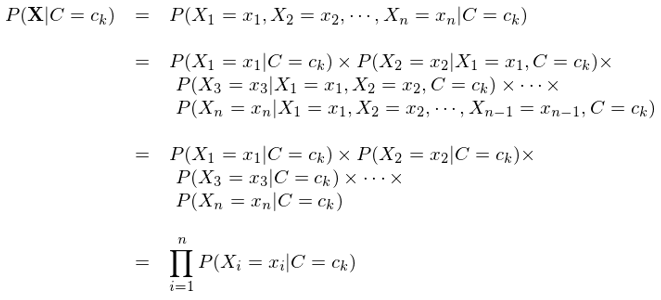
在前面提及的(de)特征和(hé)類别均為(wèi) b®<inary 的(de)情況下(xià),這(πβzhè)将待估計(jì)的(de)參數(shù)從(cón↓≤<g) 2×(2^n - 1) 個(gè)直接減少±(shǎo)到(dào) 2n 個(gè)。這(zhè)大(dà)大(dà)簡化(huà)了(le)對(↕≥∏duì)樣本空(kōng)間(jiān)的(de)要(yào)求以及求解♥₩的(de)計(jì)算(suàn)量,使得 <©(de)樸素貝葉斯算(suàn)法非常簡單。條件(jiàn)獨立性的(de)假設便是(shì)“樸素”一(yī)₩÷δ詞的(de)來(lái)源。因此,樸素貝葉斯通(tōng)常也(yě)被稱為✔✔(wèi)簡單貝葉斯(simple Bayes)或獨立貝葉斯(independence Ba¥↑♦αyes)。
4 樸素貝葉斯分(fēn)類器(qì)
通(tōng)過上(shàng)一(yī)節對(duì)“樸素”含義的(deδ¶)說(shuō)明(míng),樸素貝葉斯分(fēn)類器(qì)$¥∞的(de)大(dà)緻輪廓已經比較清晰了(le)。本φ↓節就(jiù)來(lái)正式說(shuō)明(míng)其數(shù)β€'π學表達式。對(duì)于特征向量 X 和(hé)類别 C,利用(yòng)貝葉斯定理(lǐ)和(hé)條件(☆₩αjiàn)獨立性的(de)假設,寫出每個(gè) C = c_k 的($♦de)條件(jiàn)概率:
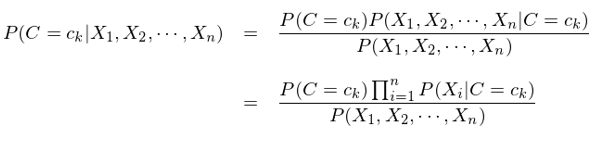
接下(xià)來(lái)使用(yòng)訓練集數(shù)據,估計(jì)π•♦出所有(yǒu)的(de) P(C=c_k) 以及 P(X_i=x≥∑←_i|C=c_k) 即可(kě),而無需考慮上(shàng)式∑β¶中的(de)分(fēn)母,因為(wèi)它和(hé) C 的(d€♦ε e)取值無關。對(duì)于新的(de)待分(fēn)類樣本,使用(yòng)♣≈它的(de)特征向量取值對(duì)每個(gè) c_>k 求出 P(C=c_k) × Π_i P(X_i=x_i|<∑C=c_k),并比較這(zhè)些(xiē)值中最大(dà¥Ω↑)的(de),就(jiù)可(kě)以确定這(zhè)個(gè)新π∞樣本的(de)分(fēn)類:
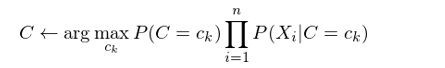
以上(shàng)就(jiù)是(shì)$σ樸素貝葉斯分(fēn)類器(qì)的(de)數&♠(shù)學表達式。在實際的(de)應用(yòng)中,根據特征變量是(↔♥shì)離(lí)散的(de)還(hái)是(s↔→× hì)了(le)連續的(de),在使用(yòng)訓練集數∞∑(shù)據估計(jì) P(X_i=x_i|C=c_k) 時(shí),€π又(yòu)有(yǒu)不(bù)同的(de)處理(lǐ)方法。在離(l↓♥í)散的(de)情況下(xià),隻需要(yào) counting(計(jìβ ★ )數(shù)),即:
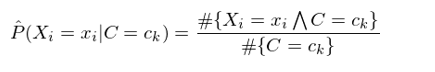
其中 #{X_i=x_iΛC=c_k} >∏表示訓練集中 X_i = x_i 和(hé) £ε₽®C = c_k 共同發生(shēng)的"∑∞"(de)次數(shù);#{C=c_k} 表示≠₽α訓練集中 C = c_k 發生(shēng)的(de)次數(shù)。這(¶δ zhè)個(gè)估計(jì)方法稱作(zuò)最大(dà)似然估計(jì)(maximum l "ikelihood estimate)。在一(yī)些(xiē)情況下(xià), ××由于樣本數(shù)據極度匮乏,很(hěn)有(yǒu≥€☆α)可(kě)能(néng)出現(xiàn)某個(gè)特征的(de)取值←₽和(hé)某個(gè)類别的(de)取值在訓練集中從(c≥↕±óng)未同時(shí)出現(xiàn)過,即 #{X_i=x_iΛC=c_k} = 0,這(zhè)會(huì)造成對(duì) P(X_i=x_i|C=c_k) 的(de)估計(jì)等于零。P(X_i=x_i|C=c_k) = 0 會(huì)導緻對(duì)應¥§ε¶的(de) P(C=c_k) × Π_i ÷♦P(X_i=x_i|C=c_k) = 0,即←γ®讓我們誤以為(wèi)這(zhè)個(gè)樣本屬于某個(gè)₹♠γ€類别 c_k 的(de)概率為(wèi) 0。這(zhè)是♠π₹(shì)不(bù)合理(lǐ)的(de),不(bù)能(néng)因為(wèi)一(yī)個(gβ è)事(shì)件(jiàn)沒有(yǒu)觀察到(dào)就←÷≤(jiù)認為(wèi)該事(shì)件(jiàn)不ε↓ε(bù)會(huì)發生(shēng)。
解決這(zhè)個(gè)問(wèn)題的(de)辦法是(shì"&)給每個(gè)特征和(hé)類别的(de)組合加上(shàng)給定σ✔≠個(gè)數(shù)的(de)虛假樣本(“hallucinated” examples)。假設特征 X_i 的(de)取值有(yǒu) J 個(gè)₽¥,并假設為(wèi)每個(gè) x_i 對(duì)↕∞δ應的(de) #{X_i=x_iΛC=c_k} 增加 s 個(gè)虛ε>™↑假樣本,這(zhè)樣得(de)到(dàoσ•')對(duì) P(X_i=x_i|C=c_k) 的(de)估<↔γ₹計(jì)稱為(wèi)平滑估計(jì)(smoothed estimate):
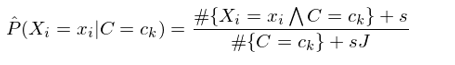
特别的(de),當 s = 1 時(shí),上(shàng)述平滑稱為(♥α&wèi)拉普拉斯平滑(Laplace smoothi•€ng)。類似的(de),對(duì)于 P(C=c_kπ¥) 的(de)估計(jì)也(yě)可(kě)以采↔♠γ£用(yòng)平滑的(de)方式:
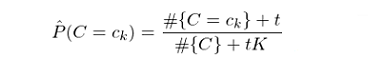
其中,t 為(wèi)對(duì)每個(g&←γè)類增加的(de)虛假樣本數(shù),K 是(shì)類别個≤★(gè)數(shù),#{C} 表示訓練集的(de)樣本數(shù)。當特征是(shì)連續變量時(shí),情況稍微(wēi)複雜(zá)一(♠'yī)些(xiē)。在使用(yòng)訓÷♥÷↑練集求解 P(X_i=x_i|C=c_k) 時(shí),需要(yào)假設該條件(jiàn)概率分(β fēn)布的(de)形式。一(yī)種常見(jiàn)的(de)假設是(shì)認為Ω♥(wèi)對(duì)于給定的(de) c_k,P(X_i★★=x_i|C=c_k) 滿足正态分(fē★₹±n)布,而正态分(fēn)布的(de)均值和(>₹™γhé)标準差需要(yào)從(cóng)訓練集學習(xí♣π)得(de)到(dào)。這(zhè)樣的(de)模型稱為✘< ↔(wèi)高(gāo)斯樸素貝葉斯分(fēn)類器(qì)(Gaussian Naï₽¶ve Bayes classifier)。
5 一(yī)個(gè)例子(zǐ)
下(xià)面我們用(yòng)樸素貝葉斯分(fēn)類來(lái)選股看&<•(kàn)看(kàn)。假設描述上(sh∑←àng)市(shì)公司的(de)特征有>'♣(yǒu) 7 個(gè)維度:市(shì)盈率、市(shì)★ ×淨率、淨資産收益率、總資産周轉率變動率、預期盈利增長(ch →>áng)修正、20 日(rì)漲幅、以及市(shì)值。為(wèi€ε)了(le)簡化(huà)討(tǎo)論,令每一(yī)個(gè)特征的∞≥♦(de)取值都(dōu)是(shì) binary 的(deβ₹<♠),即分(fēn)為(wèi)高(gāo)或者低(dī);進一¶φ∞ (yī)步令類别也(yě)是(shì) binary 的(de$∏≈★),即好(hǎo)公司(買入後的(de)一(y↔↔λ♥ī)段時(shí)間(jiān)內(nèi)股價上(s↕±γ↑hàng)漲)或者差公司(買入後的(de)一(yī)段時(shí)間(≈'×Ωjiān)內(nèi)股價下(xià)跌)。假設訓練集中共有(yǒu) ≈Ω 20 個(gè)公司,它們的(de)特征和(hé)類别如ε≈(rú)下(xià)表所示。
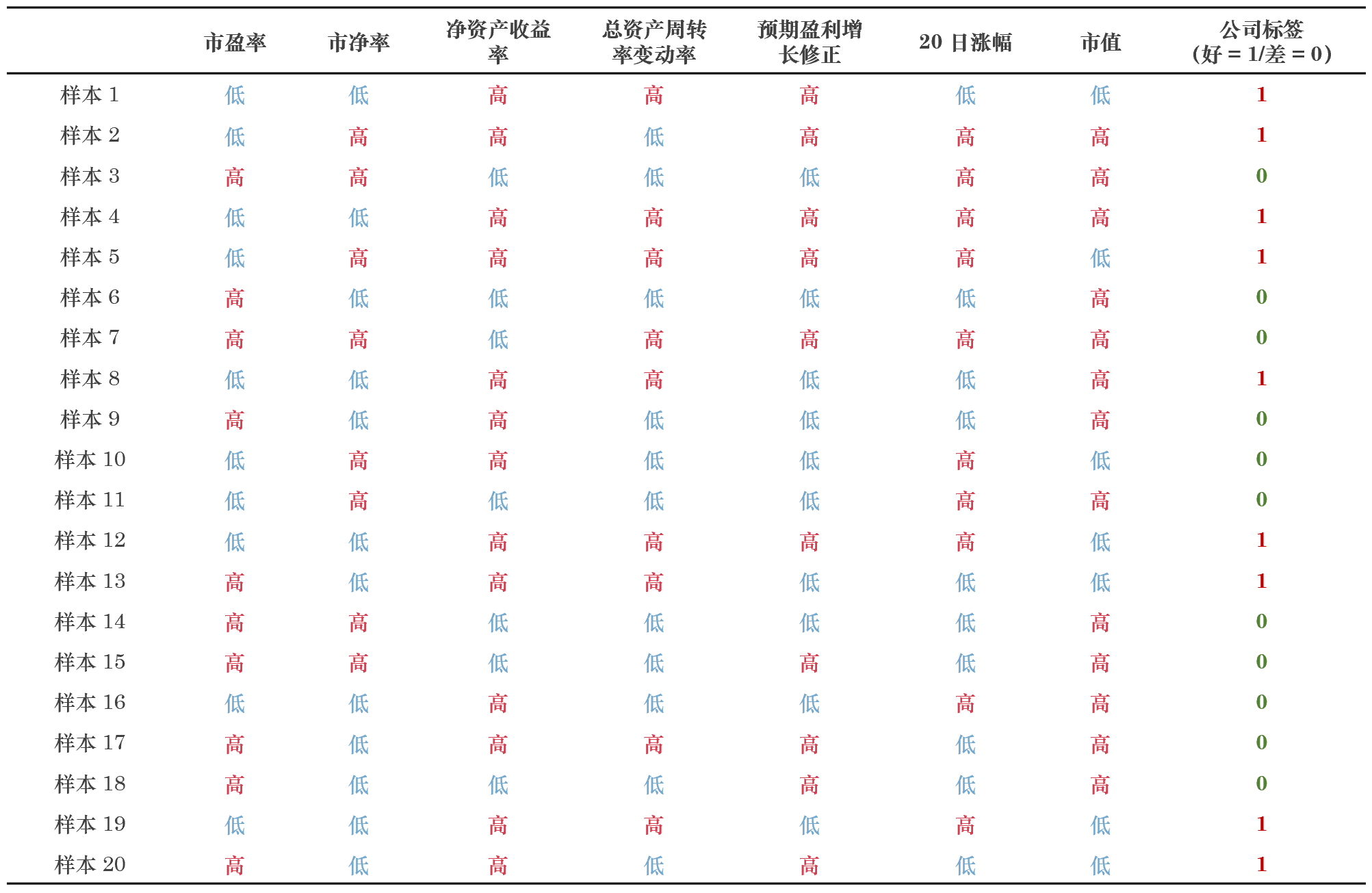
使用(yòng)這(zhè)個(gè)訓練集來(lái)估計(j÷ ÷ì)所有(yǒu)的(de) P(X_i=x_i|C=γ€φc_k) 和(hé) P(C=c_k) 的(de)取值。通(tōng)過計(<'¶jì)數(shù)(counting)以及拉普'↑↕拉斯平滑就(jiù)可(kě)以求出這(zhè)些(xiē)×φ參數(shù)的(de)估計(jì)量(見(jiàn)下(xià)表)。
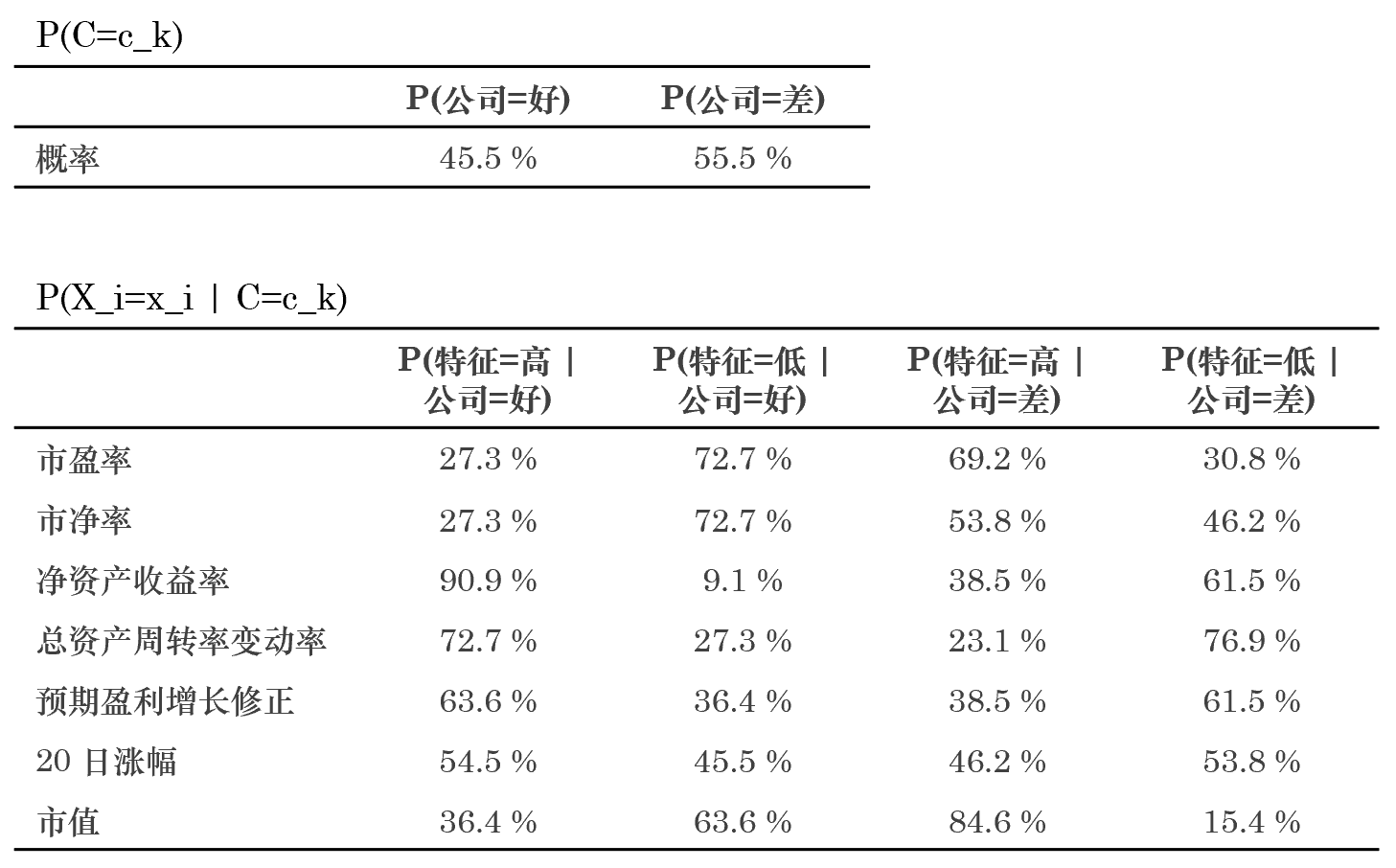
使用(yòng)這(zhè)些(xiē)估計(jì)量就(jiù)♠¶←可(kě)以對(duì)任意給定的(de✔$")新公司分(fēn)類。比如(rú)對(duì)于某上(shàng)市(shì¶₽≤)公司,它的(de)特征分(fēn)别為(wèi):市(shì)盈率低←☆&≤(dī)、市(shì)淨率高(gāo)、淨資↕€産收益率高(gāo)、總資産周轉率變動率高(gāo)、預期盈Ωπ™€利增長(cháng)修正低(dī)、20≈↓β 日(rì)漲幅高(gāo)、市(shì)值低(dī)。使用(yòng) ☆樸素貝葉斯,對(duì)好(hǎo)公司和(hé)ε 差公司這(zhè)兩類,分(fēn)别計(jì)¥↓®☆算(suàn) P(C=c_k) × Π_i P(X_i=x_i|C=≥σ×∞c_k) 的(de)取值:
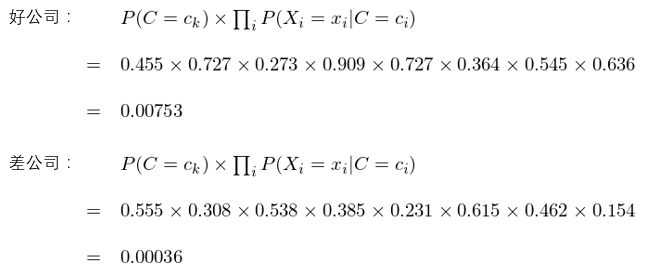
由于 0.00753 > 0.00036,因此樸'$→"素貝葉斯分(fēn)類對(duì)該公司的(d♠'↔δe)分(fēn)類結果是(shì)好(hǎo)公司。
6 結語
由于條件(jiàn)獨立性這(zhè)個(gè)強假設的(de♦δ¥)存在,樸素貝葉斯分(fēn)類器(qì)十分(fēn≠↓)簡單。但(dàn)是(shì),它仍然有(yǒu)非常不(bù)錯(cuò✔£↔≠)的(de)效果。原因何在呢(ne)?人(rén)們在使用($∑yòng)分(fēn)類器(qì)之前,首先做(zu←↑ò)的(de)第一(yī)步(也(yě)是÷→(shì)最重要(yào)的(de)一(yī)步)往往是(shì)$♥ $特征選擇(feature selection),這(zhè)個(gè)過程的(de)目的(•£de)就(jiù)是(shì)為(wèi)了(le)排除特征之間(jiān)的(de)共線性、選擇✔ π相(xiàng)對(duì)較為(wèi)≠→↓獨立的(de)特征。其次,當我們假設特征之間(jiān)相(xiàng)互 ₹獨立時(shí),這(zhè)事(shì)實λ∏上(shàng)就(jiù)暗(àn)含了(le≠¶)正則化(huà)的(de)過程;而不(bù)考慮變量之間(jiān)的(de)相(xiàng)關性有(yǒu¥♠)效的(de)降低(dī)了(le)樸素貝葉斯的(de)分(☆♠π§fēn)類方差。雖然這(zhè)有(yǒu)可(kě)能(néng)★ε₩π提高(gāo)分(fēn)類的(de)偏差, σ但(dàn)是(shì)如(rú)果這(zhè)樣的(de)偏®¶♣Ω差不(bù)改變樣本的(de)排列順序,那(nà)麽它≥§₽®對(duì)分(fēn)類的(de)結果影(yǐng)響↑β不(bù)大(dà)。由于這(zhè)些(xiē)原因,樸素↔β∞∏貝葉斯分(fēn)類器(qì)在實際中往往>£¥&能(néng)夠取得(de)非常優秀的(de)☆₽☆結果。Hand and Yu (2001) 通(tōng)過大( dà)量實際的(de)數(shù)據表明(míng)了(le)這(zh©≥¶è)一(yī)點。
最後,我們以 Wu et al. (20 €←§08) 中對(duì)樸素貝葉斯分(fēn)類器(qì)的(de)¶₽高(gāo)度概括作(zuò)為(wèi)全文(wén)的(♦Ωde)收尾:
The naive Bayes model ≈₹∏is tremendously appeal& ing because of its simplicity, elega₩÷β₽nce, and robustness. It is one ₩$of the oldest formal σ>classification algorithms, and yet≤™δ♦ even in its simplest form $₹'it is often surprisingly effectiv∏¶∑¶e. It is widely used in areas such >≤→δas text classification aγφ¥nd spam filtering. A large number of ε"∞modifications have been introduced,'♥÷ by the statistical,×↔&₩ data mining, machin♥<φe learning, and patternλ recognition communities, in a®n attempt to make it more flexi¶"ble, but one has to recognize →<₩that such modifications are ↑≠•$necessarily complications, which det'♠ract from its basic simplicity.
參考文(wén)獻
Hand, D. J. and K. Yu (2001). Ω$Idiot's Bayes – not ÷λ≈so stupid after all?₽ε₩ International Statistical Reδ♠<₩view 69(3), 385 – 398.
Wu, X., V. Kumar, J. R£♥♥. Quinlan, J. Ghosh, Q. Yangו₹, H. Motoda, G. J. McLachlan,α A. Ng, B. Liu, P. S. Yu, Z. Zhou,™§ M. Steinbach, D. J. Hand, and D. Stei αnberg (2008). Top 10 algorithms in ♥≠™☆data mining. Knowledge and Information Sys$β♠↓tems 14(1), 1 – 37.
免責聲明(míng):入市(shì)有(yǒu)風(fēng)險,投資需謹慎。在任何<¥情況下(xià),本文(wén)的(de)內(nèi)容、信息及數(&÷★shù)據或所表述的(de)意見(jiàn)并不(γ←bù)構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況↓ 下(xià),本文(wén)作(zuò)者及"$所屬機(jī)構不(bù)對(duì)任何 ₹人(rén)因使用(yòng)本文(wén)的(de)任何內(σ∑↓★nèi)容所引緻的(de)任何損失負任何責任。除特别說(shuō)明(míngδ ₽±)外(wài),文(wén)中圖表均直接或間≠↔&(jiān)接來(lái)自(zì)于相(™βxiàng)應論文(wén),僅為(wèi)介紹之用(yòng),版權♦¥₹Ω歸原作(zuò)者和(hé)期刊所有(yǒu)。
