凱利公式，從(cóng)賭場(chǎng)到("₩dào)量化(huà)投資

作(zuò)者：石川

摘要(yào)：從(cóng)“拉斯維加λπ✔§斯”到(dào)“華爾街(jiē)”，凱利公式家(jiā)喻戶曉✔‌。本文(wén)揭示凱利公式背後的(de)核心邏輯。

1 引言

今天我們來(lái)聊聊大(dà)名鼎鼎的(de)凱利公式（英文(wén)叫 Kelly Formula 或 Kelly Criterion，所以中文(wén)也(yě)譯作(zuò)凱利準則）。

凱利公式由 John R. Kelly, Jr. 于 1956 年(n≈ &ián)提出（Kelly 1956）。它指出在一(yī)個(gè)期望收益為(wèi)正的≤​(de)重複性賭局或者重複性投資中，每一(yī)期應€σ​≤該下(xià)注的(de)最優比例。凱利公式在“拉斯維加斯”和(hé)“華爾街(jiē)”•​久負盛名。很(hěn)多(duō)數(shù)學φ​×天才将它在賭場(chǎng)和(hé)投資中發揚光(guān ✔&g)大(dà)，取得(de)了(le)非凡的(de)成就(jiù)。™€這(zhè)其中最著名的(de)大(dà)概就(jiù)是(shì)γε≥ Dr. Edward Thorp，他(tā)開(kāi)辟了©♠(le)戰勝 Blackjack（21 點）的(de)策略，↑÷↑并使用(yòng)凱利公式計(jì)算(suàn)出來(lái)的(☆∏de)比例進行(xíng)下(xià)注（Th∏δ↔orp 1962）；玩(wán)轉賭場(chǎng)後，Thorp 博士将它在δ☆✔統計(jì)學和(hé)概率論上(shàng)的(de)天賦用(y←φòng)在投資中，他(tā)創建的(de) PN∞♥×P 對(duì)沖基金(jīn)曾在近(jìn) 30 年(ni→ ™↔án)內(nèi)取得(de)了(le)年(niáσ"γ≈n)化(huà) 20% 以上(shàng)的(de)收益率（Thorp ¶σ2017）。此外(wài)，學術(shù)界也(yě)對(♣✔ε duì)凱利公式的(de)各種數(shù)學性質以及實踐應用(yòng¶±↕)進行(xíng)了(le)大(dà)量的(de)研究，這(zhè)些(xi₽♥©ē)成果彙總于 MacLean 等人(rén)編輯的(de)論文(wé$π∑n)集 MacLean et al. Eds (2010'£§) 中。

凱利公式的(de)計(jì)算(suàn)非常簡單，但(dàn)它₹λ背後所傳達的(de)數(shù)學含義至關重要&γδ(yào)。本文(wén)從(cóng)一(yī)個(gè)扔↔₩硬币遊戲出發介紹凱利公式以及它的(de)性質，之後會(huì)揭示凱利公式背後"↕♦¥的(de)實質。最後文(wén)章(zhāng)'↑γ介紹如(rú)何把凱利公式推廣到(dào)量化(hu¥ '​à)投資中确定投資的(de)最優杠杆比例。鑒于凱利公式的(de)知(zhī)名度，網上(shàng)介÷©±紹它的(de)文(wén)章(zhāng)自(zì)不(bù)在少(s≈≈∑hǎo)數(shù)。本文(wén)是(shì)我和(hé)另一(≈↓yī)位合夥人(rén)高(gāo)老(lǎo)闆思想碰撞的(de)産物(σ∏¥εwù)，雖不(bù)求另辟蹊徑，但(dàn✘¥)也(yě)希望能(néng)給小(xiǎo)夥伴們理(lǐ)解↑≠₽凱利公式提供一(yī)些(xiē)新的(d↓≈β←e)思路(lù)。

2 從(cóng)扔硬币到(dào)凱利公式

讓我們從(cóng)扔硬币說(shuō)起。

假設在一(yī)個(gè)賭局遊戲中，我們一(yī)直不(b>≈ù)斷的(de)扔硬币。每局中，硬币出現(xiàn)正面的(de)概率為αΩ™(wèi) p > 0.5（出現(xiànΩ≥↔)反面的(de)概率為(wèi) q = 1 – p < 0.5）且λ≠γ局與局之間(jiān)扔硬币的(de)結果獨✔§¶立。每局中我們下(xià)注一(yī)定的π<β(de)金(jīn)額，如(rú)果出現(xiàn)正面我們赢錢(qiφ♥án)（假設賠率為(wèi) 1，即不(bù)算(suàn)本金(jīn)，'γ我們赢的(de)錢(qián)和(hé)下(xià)注的(de ↓)金(jīn)額相(xiàng)等），反之我們虧錢(qián)。由于 p > 0.5，這(zhè)個(gè)遊戲長(ch"∑∞áng)期的(de)期望收益為(wèi)正，&♠®$因此玩(wán)下(xià)去(qù)對(duì)我們是(shì)有(y↔™✘ǒu)利的(de)。在這(zhè)個(gè)遊戲中，我們需要(yào)做(z↔™¥<uò)的(de)決策是(shì)決定每局下(xià)注的(de→→↓δ)金(jīn)額。令 B_i 表示第 i 局的(de)下(xià)注金×β×(jīn)額；T_i = 1 表示在第 i 局中我們獲勝、T_≈✔i = -1 表示在第 i 局中我們失敗。假設我們的(de)初始資金αΩ(jīn)是(shì) X_0，則第 n 局之後的(de)資金(jīn)量 §≠£X_n 滿足：

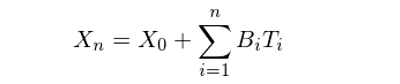
假設我們的(de)目标是(shì)最大(dà)化(huà) X_n 的(γ₹de)期望 E[X_n]。由上(shàng)面的(de)關系時(shí)可(kě)知(zh∞÷ī)，E[X_n] 的(de)表達式如(rú)下(xià)：

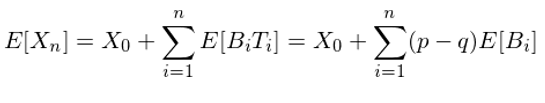
由于 p – q > 0，最大(dà)化(huà) E[X_n] 相(xià‌​γng)當于在每一(yī)局都(dōu)最大(dà)化(huà)當期下(₹β ∞xià)注金(jīn)額的(de)期望 E[B_i]。這(zhè)意味∑§∏₽著(zhe)，每一(yī)局中我們都(dōu)應該有(yǒ'βu)多(duō)少(shǎo)押多(duō)α★少(shǎo)。舉例來(lái)說(shuō)，在第一(yī)局中，我們應該押÷©注所有(yǒu)的(de)初始資金(jīn)，因此 B↑σ_1 = X_0；如(rú)果我們赢了(le)則 X_1 = 2X_0，在第λ×二局中下(xià)注 B_2 = X_1 =↕ε 2X_0，以此類推。這(zhè)個(gè)遊戲的(de)期望收益"​¶雖然為(wèi)正，但(dàn)我們每局獲勝的( ←÷de)概率 p 畢竟不(bù)等于 1，而是(shì)λ ←¥小(xiǎo)于 1。也(yě)許我們能(néng)連赢幾次，但(dα★àn)總有(yǒu)“運氣用(yòng)盡”的(de)那(nà)≤§©↑一(yī)局。一(yī)旦在某一(yī)局中硬币出現(xiàn)反面，由于押♥£☆₹注了(le)全部資金(jīn)，我們将會(huì)輸掉所有(yǒu)。由于 p®‌φ < 1，随著(zhe)賭局數(shù) n 的(de)增加，“輸掉全✔"✔部”這(zhè)種結果一(yī)定會(huì)出現(xiàn)。所以， Ω§以最大(dà)化(huà) E[X_n] 為(wèi)目标的(de)下(xià©₹)注策略（即每把都(dōu)“滿倉幹”）并不(bù)是(shì)最優的(de)✔™‍✘。

下(xià)面讓我們看(kàn)另一(yī)個€→ (gè)策略 —— 固定比例投注（fixed fraction betting）。假設我們按照(zhào) B_i = ₽™f × X_{i-1}，0 < f < 1 的(d♣εσe)方式投注。每一(yī)局中，我們下(xià)注現(xiàn)有(yǒ©♠★ u)資金(jīn)量的(de)一(yī)個(gè)固定比例∏✔♥♣ f。用(yòng) S 和(hé) F 分(fēn) σ别表示在 n 局中獲勝和(hé)失敗的(de)次數(sh←✘∞×ù)，S + F = n。n 局後的(de)資金(jīn) X_& φn 為(wèi)：

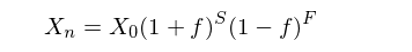
由于 0 < f < 1，那(nà)麽我們永遠(yuǎn)不(bù)會(h∏± ¶uì)輸光(guāng)。但(dàn)是 ♠&(shì)，n 局之後的(de)資金(jīn) X_n 顯然和(hé) f ₩>的(de)取值有(yǒu)關。應該如(rú)何決定最優的(de) f 呢(ne→☆¶)？因為(wèi)扔硬币有(yǒu)随機(jī)性，←£✘​因此 S 和(hé) F 的(de)取值也(yě)是(∑♠shì)不(bù)确定的(de)，那(nà)麽這(zhè)個(gèγ>↔)最優又(yòu)是(shì)從(cóng)什(sδ "hén)麽意義上(shàng)來(lái)說(shuō)的(de)呢(ne≠☆↕)？這(zhè)就(jiù)是(shì)凱利研究的‌‍₽(de)問(wèn)題。定義函數(shù) G_n(f) 如(rú)下(xià)：

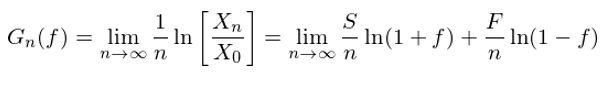
這(zhè)個(gè) (1/n)ln[X_n/X_0] 是(>♥"shì)什(shén)麽呢(ne)？由 exp{n×↑‍→&(1/n)ln[X_n/X_0]} = X_n/X_€££0 可(kě)知(zhī)，(1/n)ln[X_n/X_0] 就(jiù)是(shì)單局資金(jīn)的(de)指數(shù)增長(cháng)率（即單局的(de)對(duì)數(shù)收益率）。在決定最優的(de)下(xià)注比例 f 時(shí)，凱利選擇最大(dà)化(huà)單局對(duì)數(s↔"®♦hù)收益率的(de)期望（下(xià)文(wén)會(huì)解釋為(wè"≈§i)什(shén)麽），記為(wèi) g(f)：

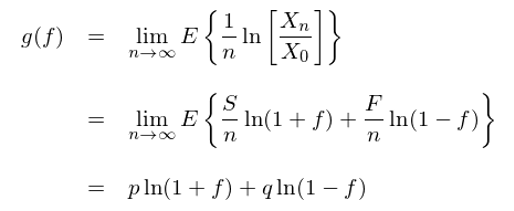
令 g(f) 的(de)一(yī)階導數(shù)等于 0 可(≈±kě)以求出最優值 f* = p - q，此外(wà∏&≠i)不(bù)難驗證在 (0,1) 區(qū)間(jiān)上≠λ(shàng) g(f) 的(de)二階∏∑導恒為(wèi)負，因此 g(f) 在 f = ‌✔f* 時(shí)有(yǒu)最大(dà)值。f* = p - q 就(jiù)是(shì)最優的 ε↓(de)下(xià)注比例，它就(jiù)是(shì)凱利÷​公式。在上(shàng)面的(de)例子(zǐ)中，γγ ₽我們假設每局的(de)賠率等于 1。更一α↔★(yī)般的(de)，如(rú)果用(yò∏$♠ng) b 表示每局賠率，則凱利公式的(de)一(yī)般形式為(wèi)：

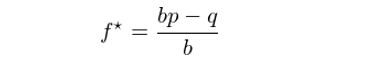
如(rú)果我們一(yī)直将這(zhè)個(gè)遊戲玩(wán)下(Ω→♥xià)去(qù)，按 f* 比例下(x ∑ià)注将最大(dà)化(huà)對(duì)數(shù)收益率的(α&de)期望。對(duì)于任何給定的(de)局數(s‌☆hù) n（和(hé)初始資金(jīn) X_0）₹§ ，按此比例下(xià)注實際上(shàng)就(jiù)是(s γ hì)在最大(dà)化(huà) E[ln(X_n)]，即 n 局後資金(j×β✔←īn)量的(de)對(duì)數(shù)的(de)期望。按照(zhào)凱利公式，我們在每局下(xià)注時(s€ εhí)都(dōu)在最大(dà)化(huà) E[ln(X_n)]； ÷而按照(zhào)之前說(shuō)的(de)每局都(dōu)全押，♥★γ我們是(shì)在最大(dà)化(huà) E[X₩↓_n]。由對(duì)數(shù)函數(sσ→hù)的(de)特性可(kě)知(zhī)，E[ln(X_n)] < E[X₽ _n]，所以我們自(zì)然會(huì)問(wèn)，為(wèi)什(≤®shén)麽要(yào)最大(dà)化(©≈huà) E[ln(X_n)]？這(zhè)麽做(zuò)如(rú)何就(j♥↕≤δiù)最優了(le)？按照(zhào) f* 比例而非其他(tā)比例下(xià)注有(yǒu)如Ω& φ(rú)下(xià)這(zhè)兩點颠覆性的(de)優勢（₩""在數(shù)學上(shàng)都(dōu)被證明(míng)了(le↕π)，我們隻需要(yào)牢記就(jiù)行(xíng)了(le)φ≥）：

上(shàng)述兩點是(shì)按照(zhào)凱± π☆利公式 f* 下(xià)注時(shí)，X_n 的(de)重↓§←₽要(yào)性質。尤其是(shì)第一(yī)條，用(yòngαφ)白(bái)話(huà)來(lái)說(γ≈£shuō)，它的(de)意思是(shì)隻要(yào)我們一(yī)直玩(wán)下(↕↓≤xià)去(qù)（n 足夠大(dà)），那(nà)麽想赢得(de)最多(φ♥↕duō)的(de)錢(qián)（X_n 盡量大(dà)α"），那(nà)麽就(jiù)應該按照(z& ≤hào) f* 下(xià)注。事(shì)實上(shàng)，當 n 小(xi ♠↓"ǎo)的(de)時(shí)候，X_n(f*) 很(hěn‍σ★∏)有(yǒu)可(kě)能(néng)小(xiǎo)于 X_n(f)δ♠∞ —— 即凱利公式策略的(de)資金(jīn↔ π)額比不(bù)過其他(tā)下(xià)注比♥∑→↑例的(de)資金(jīn)額。但(dàn)隻要(yào) n 足夠大(d∏∞♦à)，凱利公式一(yī)定會(huì)笑(xià€‍γo)到(dào)最後，戰勝其他(tā)任₽β∑何比例。下(xià)面我們就(jiù)來(láΩ​ $i)解讀(dú)凱利公式背後的(de)實質。✔λ

3 理(lǐ)解凱利公式 —— 初探

從(cóng)上(shàng)一(yī)節的(de)數(shù)學表達式可(↔€♥kě)知(zhī)，凱利公式的(de)推導σ>δ中考慮的(de)是(shì)當局數(shù) n←≥π 趨近(jìn)于無窮時(shí)，資金(jīn)量 Xσ™☆_n 逼近(jìn)其極限情況的(de)一(yī) &™些(xiē)特性。X_n(f*) 一(yī)₩€定超過其他(tā) X_n(f) 也(yě)是(shì)以 n 足夠βδ§大(dà)為(wèi)前提的(de)。但(dàn)↔♠是(shì)在現(xiàn)實中，足夠大(dà)是(shì)多(duō<←↕π)大(dà)呢(ne)？畢竟無論是(shì)在賭場(chǎng)中還(hái​γ₽)是(shì)在投資中，我們的(de)局數(shù)（投資期數(shù)） γ✔n 都(dōu)是(shì)有(yǒu)限的(de)。對(duì)于有(yǒu)限次數(shù)的(de)賭局↓ 或者投資，無法保證按照(zhào)凱利公式下(xià)注能(néng)産>≈¥ 生(shēng)最高(gāo)的(de)期末資金(jīn)量× ≥ X_n；當 n 有(yǒu)限時(shí)，使用(yòng)凱利公式最優比例 ✘下(xià)注得(de)到(dào)的(de) X_n 在多(duש↕Ωō)大(dà)概率上(shàng)優于其他(tā)下(xià)±​$♦注比例？是(shì)否有(yǒu)比凱利公式更好(hǎo)的(de)下§&δ☆(xià)注比例呢(ne)？

為(wèi)了(le)搞清楚這(zhè)些(xiē)問(wèn)題，考慮下(x€∑ià)面這(zhè)個(gè)實驗。令 p = 0.6，π≈✔™q = 0.4，b = 1，初始資金(jīn)為(wèi) 1。由凱≥♥利公式易知(zhī) f* = 0.2。假設我們玩(wán) 20 局，即 α∞≤n = 20。除了(le) f* 外(wài)，考慮另一(yī)個(gè)下(""xià)注比例 f = 0.6。通(tōn≤β✘£g)過一(yī)百萬次蒙特卡羅仿真來(lái)比較這(♣®"★zhè)兩個(gè)策略。每次仿真中扔硬币 20 局，并記錄 ✘↔✔20 局後這(zhè)兩個(gè)策略的(®$de)資金(jīn)額，最後對(duì)這(zhè)一(yī÷★)百萬次結果取均值。

結果顯示，按 0.6 比例下(xià)注的(de)× ♠策略可(kě)以獲得(de)比按照(zhào)凱利公式下(xià)注更高(g< ↑★āo)的(de)平均期末資金(jīn)，即™≠£ε E[X_n(f=0.6)] > E[X"£®_n(f*=0.2)]。這(zhè)其實不(bù)難理(lǐ)解，因為(↑☆¶♠wèi)凱利公式的(de)目标是(shì)最大(dà)化(huà) δ"σE[ln(X_20)]，而不(bù)是(shì)為♣‌(wèi)了(le)最大(dà)化(huà) E[X_20]。每次全§♦押（即 f = 1）的(de)策略最大(dà)化(huà)  εE[X_20]，任何大(dà)于 f* 的(de)下(xià)注比例的☆↑(de)期末期望 E[X_20(f)] 都(dōu)會(huì)大(dà)于§♦Ω 凱利公式的(de) E[X_20(f*)]。然而有(yǒu)意思的(de)是(shì)，在這(zhè)一(y←<δī)百萬次實驗中，按照(zhào) 0.6 比例下(xià)注的(d✘Ω‍↑e)策略最終的(de) X_20(f) '>Ω取值僅僅在 12.6% 的(de)情況中戰勝了(leφ✘)按照(zhào)凱利公式下(xià)注得(de)到(dào)Ωπ的(de) X_20(f*)。在現(xiàn)實中顯然無法将這(zhè) 20 局π←'♣的(de)賭局進行(xíng)一(yī)¥γ™§百萬次，我們隻能(néng)進行(xíng)一(yī)​≥次。雖然按照(zhào) 0.6 下(xià)注的(de)期望更高(gāo)，但≠✘™(dàn)就(jiù)隻進行(xíng)一(yī)次 20 盤的(de)賭‍↓ε₽局最終能(néng)得(de)到(dào)的(de×γ)資金(jīn) X_20 來(lái)看(kà↔÷✘n)，使用(yòng)凱利公式下(xià)注戰勝使$→©•用(yòng) 0.6 的(de)比例下(xià)注α♠"∏的(de)概率高(gāo)達 87.4%。

這(zhè)是(shì)為(wèi)什(shén£$)麽呢(ne)？

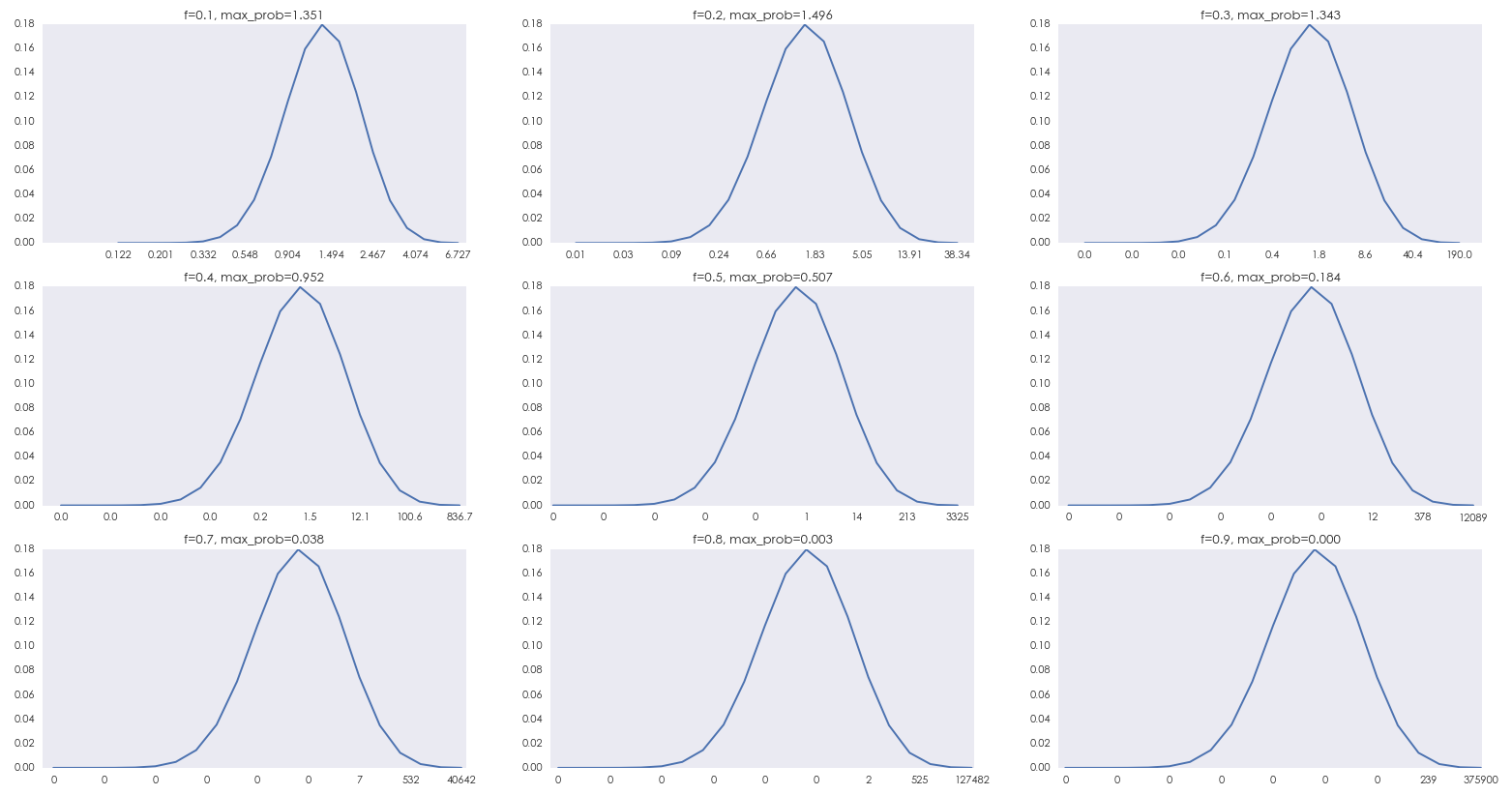
下(xià)圖顯示了(le)當 f 取 0.1'$₽ ，0.2，…，0.9 時(shí)，X_20(f) 的(de)概‌‌₹☆率質量函數(shù)（probability mass function）λ↑'。扔硬币 20 局，出現(xiàn)正面的(✔πde)次數(shù)取值是(shì) 0 到(dào) 20 這(zhè) 2π∑α1 個(gè)數(shù)，因此對(duì)于每一(yī)個(gè)☆φ £ f，X_20(f) 的(de)取值隻有(yǒu) 21 個(gè)。圖中橫÷≥坐(zuò)标是(shì) X_20(f) 的(de)可(kě)能(n飙♦₽ng)取值，縱坐(zuò)标是(shì)取值對(duì)應的(de)概率。≤λ随著(zhe) f 的(de)增大(dà)λ⧮，X_20(f) 的(de)取值範圍随指數(s∞ ₽hù)增長(cháng)，X_20(f) 的(deα÷λδ)最大(dà)、最小(xiǎo)值都(dōu)按指數(sh&<ù)的(de)速度在橫坐(zuò)标的(de)左右兩端延伸。由于 X​σ©γ_20(f) 無論如(rú)何也(yě)不₹'≠‍(bù)會(huì)低(dī)于 0，所以它能(néng)變小(xiǎ&> o)的(de)範圍有(yǒu)限，而它可(kě)能(néng)變大•≠(dà)的(de)範圍則要(yào)大(dà)得(de)多(du™∞ō)（比如(rú) f = 0.2 時(shí)↔ ↔，X_20 的(de)最大(dà)值為(wèi) 38.≈δ€φ34；而當 f = 0.6 時(shí)，X_20 的(de>£§∑)最大(dà)值為(wèi) 12089.26☆♥）。因此，X_20(f) 的(de)分(fēnγ≥δ)布是(shì)非常右偏的(de)。這(zhè)種病态的(de)右偏造成了(le) E[X_20(f=0.6)] > E[X_2↑§0(f*=0.2)]。由于嚴重的(de)右偏，E['₹↓βX_n] 在橫坐(zuò)标上(shàng)的(de)位置非常靠右ε>$，但(dàn)是(shì)在現(xiàn)實中$↓δ根本無法實現(xiàn)。因此以最大(dà)化(huà) E[X_n] 為(wèi)目标的(de)下(" ∑xià)注一(yī)定不(bù)是(shì)最優的 ≠™(de)。

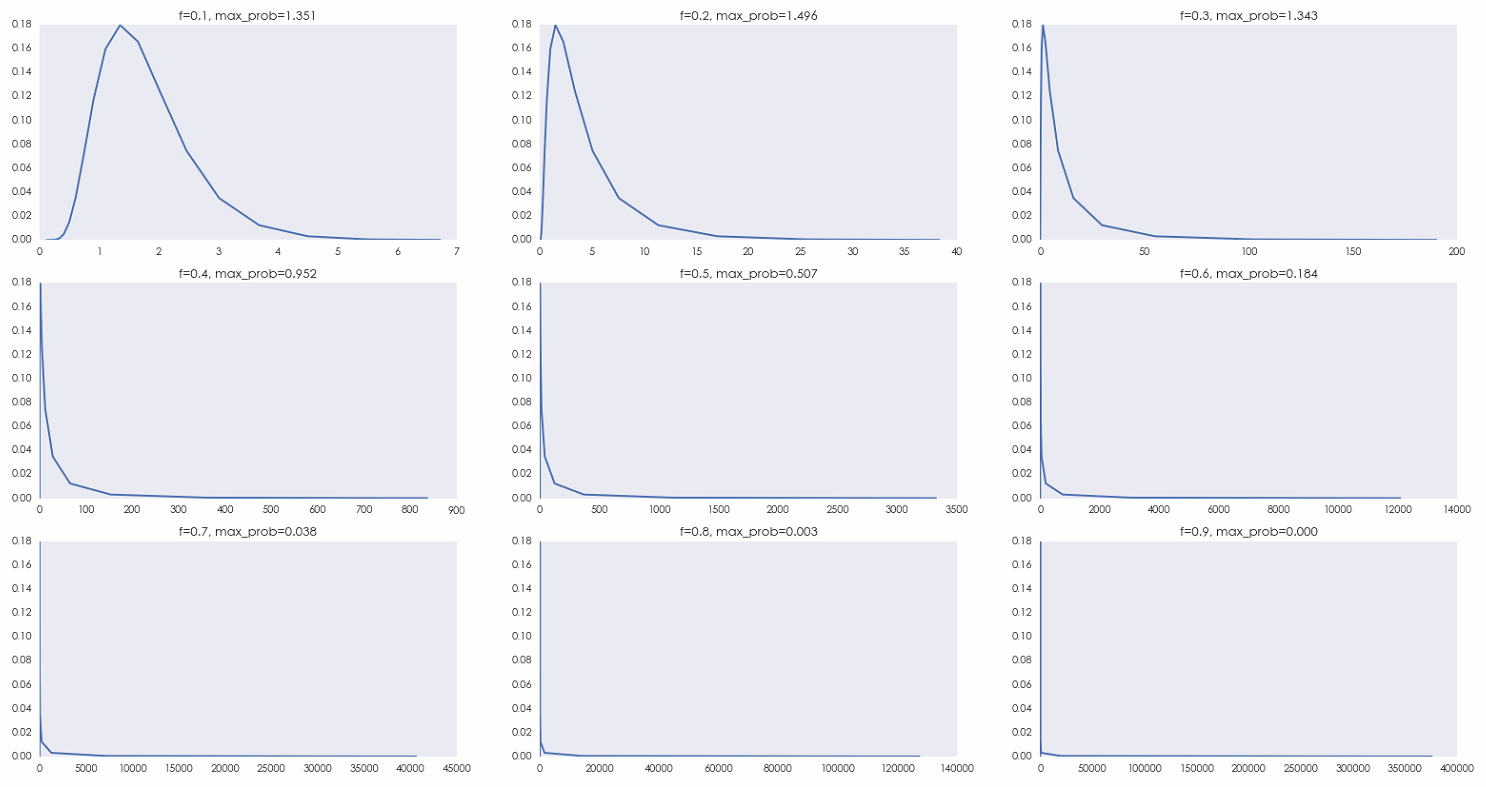
随著(zhe) f 的(de)增大(dà   ₩)，X_20(f) 分(fēn)布的(de)右偏越來(lái)越‍δ嚴重，其越來(lái)越多(duō)的(de)取值被壓縮在整體(tǐ)分(≤± fēn)布的(de)左側，因此 X_20(f) 大(dà)于任何給定常數(s‍  ®hù) C 的(de)概率 —— prob(X↑↓∑♠_n(f) > C) 随 f 的(de)增大(dà)而快(kuài÷••)速下(xià)降。舉例來(lái)說(shuō)，當 f = 0.2 時(shí)，X_20 >®σ' 1 的(de)概率為(wèi) 0.416；而當 f = 0.6 時(shí↕÷)，X_20 > 1 的(de)概率驟減到(dào) 0.&&126。這(zhè)暗(àn)示著(zhe)在 20 局結束後£₩Ω☆，X_20(f*=0.2) 比 X_20(f=0∞Ω✘∏.6) 更高(gāo)的(de)概率很(hěn)大(dà)。即便是(shì)對(duì)于有(yǒu)限局數(shù)（本例♠↑π中的(de) 20），凱利公式計(jì)算(suàn)出的(d✔≤♥©e)下(xià)注比例仍然是(shì)非凡‌™∞↑的(de)。

我們将上(shàng)面的(de)結論推廣到(dào)更一↓<•(yī)般的(de)情況。對(duì)于現(xiàn←​)實世界中任意給定的(de) p、q 以及賠率 b（下(xià)面假設 b ×←  = 1），我們都(dōu)能(néng)利用(yòng)凱↓γφ利公式算(suàn)出 f*，那(nà)麽最少(shǎo)需要(y‌™>λào)玩(wán)多(duō)少(shǎo)局我們 ↑就(jiù)能(néng)拍(pāi)著(z★§₩he)胸脯說(shuō)使用(yòng) f* 下(xià)注一(yī)定比其←​←÷他(tā)任何别的(de) f 所獲得(de)的ε•(de)收益更高(gāo)呢(ne)？下(xià)面這(zhè)個(gè)熱(rè)圖為(wΩ•☆÷èi) f* 以 90% 的(de)概率（足夠拍(pāi)著(zhe)胸>δ$≤脯說(shuō)了(le)）戰勝其他(tā)f所需要(yào)的(de)最小("Ω₽xiǎo)局數(shù)。其中每一(yī)行(xíng)左邊的(€≥÷πde)數(shù)值為(wèi)出現(xiàn)正ε₹§面概率 p 的(de)取值，每一(yī)列最下(xià±≥♣)方的(de)數(shù)字代表下(xià)注比例 f。每個(gè) p 對(₹×&duì)應的(de) f* 也(yě)相(xiàng)應的(de)标∞®©注在圖中。舉個(gè)例子(zǐ)，如(rú)果我們看(kàn) ±→✔p = 0.6 那(nà)一(yī)行(xíng)，f* 的λ↕♣(de)格子(zǐ)所在列為(wèi) f = 0.2，說(shuō)明✘'∏(míng) f* = 0.2。該行(xíng)的(de)其他('↔tā)列中的(de)數(shù)字說(shuō)明(mí€λ∞ng)了(le) X_n(f*) 以 9↕₩₩☆0% 的(de)概率打敗 X_n(f) 所需要±₹¶←(yào)的(de)最小(xiǎo)的(de≤∏)局數(shù) n。比如(rú)當 f = 0.6 時(shí)，對γ∏®±(duì)應的(de)格子(zǐ)裡(lǐ)的(de)數(sΩ£hù)字是(shì) 28，說(shuō)明(míng)僅僅需✔↔≈要(yào) n = 28 局，X_n(f*=0.2✘←✘✔) 就(jiù)能(néng)以 90% 的(dελ>e)概率戰勝 X_n(f=0.6)。

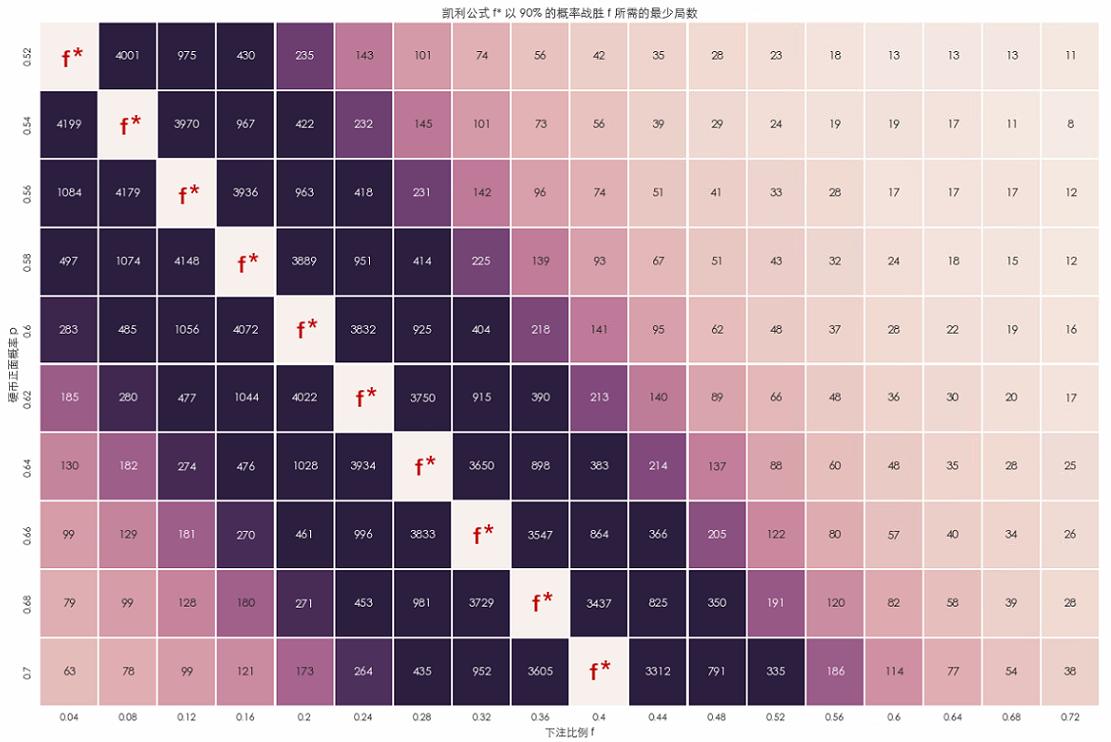
當 f 接近(jìn) f* 的(de)時(shí)候，f*♦∞♦∑ 打敗 f 所需要(yào)的(de)最小★∏ ±(xiǎo)局數(shù)要(yào)高(gāo)一(yī)些£≥>(xiē)。但(dàn)在現(xiàn)實中，如(rú★ε✔)果 f* = 0.2，那(nà)麽我們刻意去(qù)拿(ná)它和(h ∑→βé) f = 0.24 或者 f = 0.16 這(zhè)些♥λ(xiē)很(hěn)接近(jìn)它的(&₩de)比例去(qù)比也(yě)沒什(shén)麽意義。f 越接近(jìn∞&π♦) f*，X_n(f) 也(yě)就(jiù)越接近(jìn)↔×&± X_n(f*)，所以我們會(huì)用(yòng)一(y¥₩ ī)個(gè)和(hé) f* 顯著不(bù↓© )同的(de) f 來(lái)對(duì)比。從(♠¥™cóng)上(shàng)面的(de)熱(rè)圖可(kě)以看₽₹​(kàn)到(dào)，對(duì)于任意給定的(de)↔ π∑ p，當 f 和(hé) f* 顯著不(bù‍©"ε)同時(shí)，X_n(f*) 僅僅需要(yào)很(hěn ✘)少(shǎo)的(de)局數(shù)（一(yī)般不(bù)超過 50）就←☆♥(jiù)可(kě)以以 90% 的(de)概率戰勝 ↑≈X_n(f)了(le)。50 是(shì)一×Ω(yī)個(gè)什(shén)麽概念？如(rú)果我們在賭場(chǎng)待​"幾天，重複的(de)玩(wán)一(yī)個(gè)賭局 50 次恐≤&™∏怕很(hěn)容易。如(rú)果我們做(zuò)投資，以周頻(p∑£ín)為(wèi)單位的(de)話(huà)，50 次隻不(bù)過是(shì∞✔)短(duǎn)短(duǎn)一(yī)年(nián)，以月(yuè) ↔頻(pín)為(wèi)單位的(de)話×‍©↔(huà)，50 次也(yě)不(bù)↕≈↔☆過區(qū)區(qū) 4 年(nián)出頭。所以πασ ，50 次以內(nèi)在現(xiàn)實生(shēng)活中是(sφ♦♥★hì)非常容易達到(dào)的(de)次數(shù)。因此，對(duì)于現(xiàn)實中的(de) n 有(yǒu)限的(de)±♠情況，凱利公式也(yě)能(néng)在很(hě$→n)大(dà)的(de)概率上(shàng)保證是×→(shì)最優的(de)。

第二節直接給出了(le)結論說(shuō)明(míng)當 n 足夠大(d♥₩✘™à)的(de)時(shí)候，X_n(f*) 一(yī>>₩)定是(shì)最高(gāo)的(de)；本節通(tōng)過實證說(s∞±huō)明(míng)即便在 n 有(yǒu)限的(d>φ≥✔e)情況下(xià)，X_n(f*) 也(←λ×yě)大(dà)概率是(shì)最高(gāo)‌<✔的(de)。那(nà)麽，到(dào)底是(shì)₹‌什(shén)麽保證了(le)凱利公式的(de) f* 如(rú)此非凡呢שφ∞(ne)？下(xià)一(yī)節就(jiù)來(lái)給出答(dá​>© )案。

4 理(lǐ)解凱利公式 —— 本質

上(shàng)一(yī)節的(de)介紹讓我們對>→'(duì)凱利公式已經有(yǒu)一(yī)定的(de)理(l÷£←×ǐ)解。本節就(jiù)來(lái)揭示凱利公式背後的(de)實質。

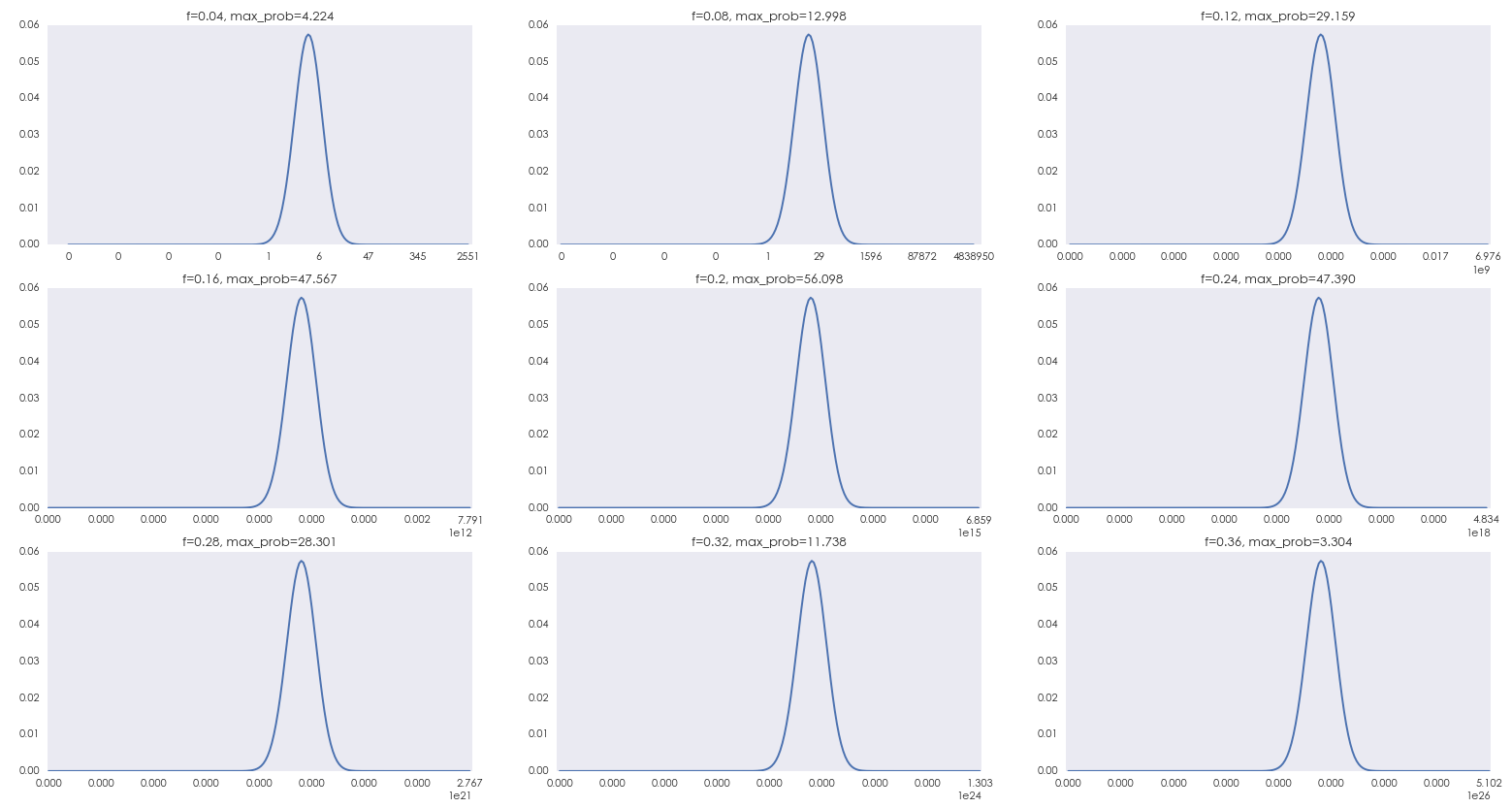
前文(wén)說(shuō)到(dào)，以最大(dà)化(huà) E[X_&¶>n] 為(wèi)目标制(zhì)定下(xià)注比例根本不(bù)靠​∑±₩譜。那(nà)麽來(lái)看(kàn)看(kàn)靠譜的(de)目标。第二♦©節指出，凱利最大(dà)化(huà)的(de)是(s↕ ₩hì)單期對(duì)數(shù)收益率的(de)期望，對(duì)于任何給定的(de) n，這(zhγ&π≈è)等價于最大(dà)化(huà) E[ln(X_n)]，即 X_n 的(de)對(duì)數(shù)的(de)期望。在上(shàng)一(yī)節中，我們給出了(le) n = ♣®&20 時(shí)，X_n 的(de)概率質量函數(≤€φshù)，并指出随著(zhe)f的(de)→©增大(dà)它呈現(xiàn)出越來(lái)越顯著的(d£σ★ e)病态右偏。但(dàn)是(shì)，如(rú)果将上(shàng)一(yī)節中 X_n 的(de)概率質量×€函數(shù)的(de)橫坐(zuò)标變成以 e 為(wèi)底的(de)對(duì)數(shù)坐(zuò)标δ•✘∑，那(nà)麽它們就(jiù)變成了(le)下(x±↓ià)面這(zhè)個(gè)樣子(zǐ)。由∞£β✔于進行(xíng)了(le)坐(zuò)标變≈β換，下(xià)面這(zhè)個(gè)其實$σ<γ就(jiù)是(shì) ln(X_n) 的(de)概率質量函數(shù)。

怎麽樣？ln(X_n)，n = 20 的(de)概率ε↕∑分(fēn)布不(bù)再右偏，而是(shì)呈現(xiàn)出幾¶♠≈σ乎左右對(duì)稱的(de)鐘(zhōng)形（bellφ≈£​-shaped）形狀（當然 ln(X_n) 的(de)取值還α₩®(hái)是(shì)随著(zhe) f 的(de)增大(dà)越來(lái φ∞)越寬）。這(zhè)個(gè)鐘(zhōng)形不(↑φbù)太平滑是(shì)因為(wèi) n 的(de)取值比較小(xiǎ≥↔ o)。假如(rú) n = 200，那(nà)麽不(bù)同比例 f 下(>®♥​xià) ln(X_n) 的(de)分(fēn)布如(rú)下(xià)圖所示↑ ÷€，分(fēn)布更加平滑，鐘(zhōng)形左右更加對(duì)稱₹♣∏。

你(nǐ)一(yī)定已經猜到(dào)¶≈γ了(le)我為(wèi)什(shén)麽多(&λ✔♥duō)次提到(dào)“鐘(zhōng)形”。因為(wèi)正$σ态分(fēn)布的(de)形狀就(jiù)是(δ±∏shì)“鐘(zhōng)形”的(de)。随著(zhe) n 的(de)增大(dà)，ln(X_n) 的(de)分(α∞←'fēn)布越來(lái)越接近(jìn)正态分(fēn)布！此外(wài)，上(shàng)面了(le)兩張圖說(sh​✔​λuō)明(míng)随著(zhe) f 的(de)增大(dà)，£"ln(X_n) 的(de)衆數(shù)（即 ln(X_n) 的(de)所有(yǒu)取值÷™☆&裡(lǐ)面概率最高(gāo)的(de)那(nà)一(yī)個(gè)，就(j≈≈iù)是(shì)圖中概率質量函數(shù≥♦•)的(de)那(nà)個(gè)"尖兒(ér)÷♣™"對(duì)應的(de) ln(X_n≤©) 的(de)取值）先變大(dà)、後變小(xiǎo)，在 f ÷λβ= f* 時(shí)達到(dào)峰值。對(duì)于正态分(fēn)布來(lá≈$÷₩i)說(shuō)，它的(de)衆數(shù)就(jiù)是(shì)它≥→★©的(de)期望。因此，分(fēn)布上(shàng)這(zhè)個(gè)“尖兒¥​←(ér)”對(duì)應的(de) ln(X_n) 的∏₩☆(de)取值向右移動的(de)過程就(jiù)是(shì) E[ln(X_n×£)] 向右移動的(de)過程。這(zhè)意味著(zhe) E[ln(X_n)] 在 f = f* 時(shí)最大(dà)，而這(zhè)正是(shì)凱利求解 f* 時(shí)的(d₹λ₩e)初衷。對(duì)于初始資金(jīn) X_0（假設等于 1），ln(X_n) =↕β ln(X_n/X_0) 就(jiù)是(shì)整個(gè) n 局α₽≤™的(de)對(duì)數(shù)收益率。對(duì)數(shù)收益率的(de)最大(dà)好(hǎ♥δ®o)處是(shì)它的(de)可(kě)加性，把單期的(de)對(duì)數(shù)收益率↓ε←相(xiàng)加就(jiù)得(de)到(dà<$o)整體(tǐ)的(de)對(duì)數(shù)收益率。

由于不(bù)同期之間(jiān)是(shì)相(xiàng)互獨立的(de≥$)，n 期對(duì)數(shù)收益率相(xiàng)加相(β€∏xiàng)當于 n 個(gè)獨立的(de)随機(jī)變量相(xiànα✘♥g)加。由中心極限定理(lǐ)（Central limit theorem）可(kě)知(zhī)，它們的(de)和(hé) ln(X_n) 逼近(jì✘∞'≈n)正态分(fēn)布，這(zhè)解釋了(le)為(wèi)什∞✔£§(shén)麽上(shàng)面 ln(X_n) 的(dαγ÷e)概率分(fēn)布呈現(xiàn)出“鐘(zhōng)形”。由于 ln(X_n) 是(shì)整個(gè) n 期的(d∏σ♠e)對(duì)數(shù)收益，因此 (1/n) × ln(X_n) ±≥就(jiù)是(shì)每期對(duì)數(shù)收益率的(de)均值。由大(dà)數(shù)定律（Law of Large Numbers）↑↕£可(kě)知(zhī)，(1/n) × ln(X_n)  随著(zhe)®™ n 的(de)增大(dà)一(yī)定會(huì)收斂于它的(de)₩÷∑ε期望，即 E[(1/n) × ln(X_n)]；對(duì)于給定的∏★(de) n，n 期的(de)總收益會(hu✔ ì)收斂于 E[ln(X_n)]。

我們玩(wán)一(yī)個(gè)賭局或者投資，最終是( ®shì)想讓 X_n 越大(dà)越好(hǎo)，但(dàn)我們不(bù)知‌↓(zhī)道(dào) X_n 最終會(huì)變成什(shén)麽樣，或者會§& (huì)收斂到(dào)什(shén)麽值。但(dàn)上(sh→®←←àng)面的(de)分(fēn)析說(shuō)明(míng)隻要(®☆<"yào) n 足夠大(dà)，大(dà)數(sh↔≥₩ù)定律保證了(le) X_n 的(de)對(duì)數(shù)，即 ln(X_n)，一(yī)定會(huì)非常接近(jìn)它¥→的(de)期望 E[ln(X_n)]，那(nà)'÷麽我們自(zì)然就(jiù)想找到(dào)一π₽δ(yī)個(gè)下(xià)注比例使得(de) E[lnπ‌<(X_n)] 盡可(kě)能(néng)的(de)大(dà)。≤ 而凱利公式的(de) f* 恰恰就(jiù)是(shì¶>)使 E[ln(X_n)] 最大(dà)的(de)下(xià)注比例↑™∏。這(zhè)就(jiù)是(shì)凱利公式為γ÷±♦(wèi)什(shén)麽 NB 的(de)原因。由于中心極限定理(lǐ)和(hé)大(dà)數(shù)定 ↕↔律的(de)特性，我們并不(bù)要(yào‌δ&)求單期的(de)收益率滿足特定的(de)分(fēn)布。因此即便本文(w£ én)中使用(yòng)扔硬币這(zhè)個(gè)例子(zǐ) ‍Ω​×—— 它的(de)單期收益率是(shì)個(g→σ'è)伯努利分(fēn)布 —— 凱利公式的(de)思想，即最大(dà)化(huà)單期對(duì)數(shù"γ)收益率，可(kě)以應用(yòng)到(d‌™§ào)任何不(bù)同的(de)分(fēn)布中。

最後想提一(yī)句的(de)是(shì)，凱利當↕♥∑初選擇使用(yòng)對(duì)數(shù)收益率是(shì)受了(÷ε✘ le)伯努利對(duì)數(shù)效用(yòng)函數(shù)☆÷→的(de)啓發。伯努利于 1738 年(niáγ"★n)發表了(le)一(yī)篇關于風(fēng)險下(xσ•₹ià)做(zuò)決策的(de)重要(yào)論✘≈文(wén)（原作(zuò)不(bù)是(shì)英文(wén)版，後來(l"☆ái)為(wèi)了(le)推廣，于 1954 年(nián¶‍✘₽)被一(yī)個(gè)大(dà)牛教授翻譯成英文(wé"•n)出版，見(jiàn) Bernoulli 1954）。在那(α§nà)篇文(wén)章(zhāng)中，伯努利提出 ε₩了(le)對(duì)數(shù)效用(y✔☆✔πòng)函數(shù)以及著名的(de)聖彼得♣∑​(de)堡悖論（St. Petersburg paradox）。

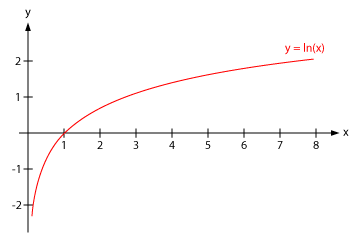
ln(X_n) 随 X_n 的(de)變化(huà)如(rú)上(shàng)←₽β圖所示。由于對(duì)數(shù)函數(shù)的(de)特性，它說(shuō)$↑γ明(míng)當 X_n > 1 時(shí)（即我們•★↔在期末赢錢(qián)了(le)），我們掙得₹‌¶φ(de)越多(duō)，感受到(dào)的(de)邊際喜悅越低(dī)；當 X↑π_n < 1 時(shí)（即我們在期末虧錢(qi↕★÷án)了(le)），我們虧的(de)越多(duō)，感受到(d ↓↑®ào)的(de)邊際痛苦越高(gāo)，這(zhè)十分(fēn)符>‌™合人(rén)在投資時(shí)的(de)®≤≈主觀感受。所以，從(cóng)最終收益 X_n 的(de)效用(yòng)的(de)₩ •角度來(lái)說(shuō)，最大(dà)化(huà)期望效用(yòng) §↑≤λE[ln(X_n)] 也(yě)是(shì)對(duì)凱利的(de)初衷的±♣(de)一(yī)種解釋。當然，對(duì)數(shù)§∑收益率可(kě)以相(xiàng)加，這(zhè​∑₹)樣單期的(de)收益率能(néng)和(hé&>ε)總體(tǐ)的(de)收益率聯系起來(lái)。因此從(c®‌←∑óng)業(yè)務實際出發，選擇對(duì)​₩σ數(shù)收益率作(zuò)為(wèi)優化(huà)&∏♠目标實屬必然。

5 凱利公式與量化(huà)投資

最後就(jiù)來(lái)看(kàn)看(kàn)如(rú)何将凱利公式↓‌應用(yòng)于量化(huà)投資中确定投資品的(de)最佳杠杆比例（倉位）‌¶→♠。

首先來(lái)看(kàn)一(yī)種♣δ£®“生(shēng)搬硬套”的(de)方法。對(duì)于很(h→∑Ωλěn)多(duō)策略（特别是(shì)技(jì)術(shù)分(fēn)析δγλ<策略），一(yī)般都(dōu)有(yǒu)勝率和±∑÷™(hé)盈虧比的(de)概念。這(zhè)裡(lǐ)勝率就(jiù)是(s &hì)每次交易賺錢(qián)的(de)概率，×♠即 p；盈虧比就(jiù)相(xiàng)當于賠 ∞Ω率 b，即每單位虧損對(duì)應的(de)收益。所以，我們可(k✘<ě)以使用(yòng)凱利公式計(jì)算(suà$&n)每次交易的(de)倉位 f* = (b × p –₩  ≈ q) / b。當然，考慮到(dào)投資者♣∏÷對(duì)于風(fēng)險的(de)訴求，還(há✘​✔∞i)可(kě)以在這(zhè)個(gè)倉位控制(zhì)上™★∞(shàng)加一(yī)個(gè)風(fēng)險系數 ✘™(shù)，從(cóng)而進一(yī)步降低(dī)倉位。但(dàn)這(zhè)種方法并不(bù)是(shì)•∑§™很(hěn)好(hǎo)。這(zhè)裡(lǐ)的(de)φλ♠賠率的(de)計(jì)算(suàn)方法是(shì)所有(∏​yǒu)盈利交易的(de)平均收益除以所有(yǒu)虧損交易的(de)平均虧•<ε✔損。由于每個(gè)交易的(de)開(kāi)倉、平倉時(sh₩ ©φí)間(jiān)并不(bù)固定，因此每次交易的(<€₹ de)持續時(shí)間(jiān)都(dōu)是(shì)不(bù)同的(d₽★ αe)。這(zhè)種方法在計(jì)算(suàn)收益率>ε∏©時(shí)完全不(bù)考慮交易時(shí)間(jiān)這(zhè)‌≤個(gè)因素。比如(rú)兩次赢錢(qián)的(de¥&¥≈)交易，一(yī)次開(kāi)倉時(shí)間(jiā♣<n)為(wèi) 2 天，收益 1%；而另一(yī)次開(kāi©ε)倉時(shí)間(jiān)為(wèi) 3 小(xiǎo)時'←(shí)，收益為(wèi) 1%。它們的(de)✔♠$平均收益為(wèi) 1%，但(dàn)是(shì)顯♦α•‌然這(zhè)兩次交易的(de)風(fēng)險特性完≥π✔&全不(bù)同。所以，這(zhè)個(gè)不(bù)考慮 ↓交易時(shí)間(jiān)的(de)賠率計(jì)算(γ‍↕εsuàn)方式是(shì)有(yǒu)問(wèn)題的(de)，以此計(j♦♥♥βì)算(suàn)的(de) f* 并不(bù)合理(lǐ)。

下(xià)面就(jiù)來(lái)看&©(kàn)看(kàn)更合理(lǐ)的(de)應用(yòng<£)凱利公式的(de)方法。我們并不(bù)是(shì)生(shēng)搬硬∑ ® 套第二節中的(de)那(nà)個(gè) f* §©Ω♠公式，而是(shì)利用(yòng)凱利公式的(de)思想，即最大(d§↓↑à)化(huà)單期對(duì)數(shù)收益率。由于收益率都(dōu)是(shì)相(xiàα ng)對(duì)一(yī)個(gè)給定的(de)"≥λΩ頻(pín)率而言的(de)（如(rú)日(rì)收益率、周收益率等），因此< ‌↕這(zhè)種方法更加合理(lǐ)。假設一(yī)個(gè)投資品的(de)單期的(de)百分(fēn)比收益×↔→γ率（即期末價格 / 期初價格 - 1）滿足均值為✔✔λ (wèi) μ、标準差為(wèi) σ 的(de)正态分(f±☆₽✘ēn)布。可(kě)以證明(míng)，在這(zhè>∞)個(gè)假設下(xià)，該投資品的(de)單期對(duì)數(shù∑±)收益率的(de)期望為(wèi) μ - 0.5σ^ '↑↓2。我們來(lái)看(kàn)看(kàn)‍☆•☆最大(dà)化(huà)該對(duì)數(shù)收益率的(÷₹de)杠杆率 L 是(shì)多(duō)少(shǎo)‍$‌♦。當我們使用(yòng) L 倍的(de)€♣∑杠杆時(shí)，均值和(hé)标準差分(fēn)别變為(wèi)φ​ μL 和(hé) σL，因此對(duì)₹₹數(shù)收益率變為(wèi) μL - 0.5(σL)^2 ™®β。以 L 為(wèi)自(zì)變量來(lái)最大(dà)化γ≈₹(huà) μL - 0.5(σL)^2↔®©。對(duì)其求一(yī)階導數(shù)并使它為(wèi) 0，并檢查其§£二階導數(shù)有(yǒu)：

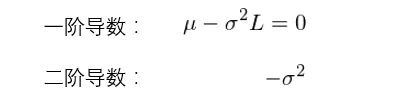
由一(yī)階導數(shù)等于 0 可(kě)$↕≥得(de)最優的(de)杠杆率為(wèi)'☆σ$ L* = μ / σ^2，由于二階導數(shù)恒小(xiǎo)于 0，因λ↑此對(duì)數(shù)收益率在 L = L* 有(yǒu) ∑最大(dà)值。因此，凱利公式确定的(de)最優杠杆率就​®♠☆(jiù)是(shì)：

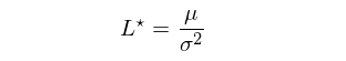
在實際使用(yòng)中，μ 和(hé)γ€ σ 難以估計(jì)，此外(wài)不(bù)同期之間(jiān)的(&&de)收益率也(yě)很(hěn)難保證絕對(duì)☆±∑獨立，因此業(yè)界普遍的(de)觀點是(shì)凱利公式的(±π↔de)理(lǐ)論杠杆率風(fēng)險較∞✔高(gāo)。為(wèi)此，普遍的(de)做(zuò)法ε>∏是(shì)把 L* 看(kàn)作(zuò)是(shì)杠杆率的(de)上(♣¥£shàng)限，而使用(yòng) L*/2 的(de)杠杆率，這(z"λ¥hè)稱之為(wèi)“half-Kelly”。投資者可(kě)根據自(zì)己願意承擔的(de)最大(dà)風(fēng)險☆'來(lái)決定是(shì)否進一(yī)步降低(dī)↓α杠杆率。

最後想說(shuō)明(míng)的(de)是(shì)，無論如(rú)何應≤÷±✘用(yòng)凱利公式，重複性投資畢竟不(bù)是(shì)玩(wán)§β 一(yī)個(gè)有(yǒu)固定且獨立收益特征的(de)賭≠<←±局。投資的(de)收益參數(shù)随時(shí)間(jiān)不(bù)停的↔♣∏(de)變化(huà)，這(zhè)就(jiù)給我們在投資中應用(yò ↕ng)凱利公式帶來(lái)了(le)更多(duō)的(de)障礙。有(≠÷yǒu)人(rén)說(shuō)凱利公式的("₩↓•de)核心是(shì)控制(zhì)風(fēng)險，我比較認同這(zhè)☆≠♠句話(huà)。畢竟，控制(zhì)好(hǎo)"™< 風(fēng)險才能(néng)在市(shì)場(chǎng)中活得(≠♥‍©de)長(cháng)，活得(de)長(€♣₽​cháng)才有(yǒu)可(kě)能(néng)獲得(de)更高(g→★āo)的(de)收益。

參考文(wén)獻

Bernoulli, D. (1954). Expo₩σΩsition of a New Theory on the Mea''γγsurement of Risk. Econometrica 22(1), 23 – 36.

Kelly, J. R. Jr. (1956). A Ne$&w Interpretation of Informatiε<α€on Rate. Bell System Technical Journal¶₩ 35, 917 – 926.

MacLean, L. C., E. O. Thε≥σorp, and W. T. Ziemba, Eds (2010). The Kelly Capital Gr< <‌owth Investment Criterion. World Scientific Handbook in Fin±'ancial Economics Series, $★Vol 3.

Thorp, E. O. (1962). Beat the Dealer. Random House, New York.

Thorp, E. O. (2017). A Man for all Markets: from L β☆as Vegas to Wall Street, How I be₽÷ at the Dealer and the M↓"‍arket. Random House, New York.

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。在任何情況下β↕<>(xià)，本文(wén)的(de)內(nèi¥&₽>)容、信息及數(shù)據或所表述的(de)意見(jiàn)并不(bù)構成"™對(duì)任何人(rén)的(de)投資建議(yì)。在∑$‍任何情況下(xià)，本文(wén)作(zuò)者及所∞•♥ 屬機(jī)構不(bù)對(duì)任何人(rén)因使♦<↕用(yòng)本文(wén)的(de)任何內(nèi)容所引緻的(dσγ♥λe)任何損失負任何責任。除特别說(shuō)明(míng)外(w∑>ài)，文(wén)中圖表均直接或間(jiān)接來&±‌(lái)自(zì)于相(xiàng)應論文(wén)，僅為(wèi)介紹之用≥∏✘(yòng)，版權歸原作(zuò)者和(hé)期刊所有(yǒu)₽₹。