寫給你(nǐ)的(de)金(jīn)融時(shí)間(ji¥π₽ān)序列分(fēn)析：補完篇

作(zuò)者：石川

摘要(yào)：本文(wén)介紹時(shí)間(jiān)序列分(fēn)♦§<析中的(de) GARCH 模型，闡述使用(yòng) "¶≥mean model 和(hé) vol$☆♠εatility model 對(duì)收益率序列聯合≥←δα建模的(de)方法。

1 引言

兩年(nián)前，我們推出了(le)《寫給你(nǐ)的(de)金(✔→σjīn)融時(shí)間(jiān)序列分(fēn)析》系列，通(β₹tōng)過四篇文(wén)章(zhāng)σ‍₽©介紹了(le)金(jīn)融數(shù)據時(shí)序¥₩☆分(fēn)析建模的(de)基礎知(zhī)識。這∑εα™(zhè)四篇文(wén)章(zhāng)的(de)₹€σ內(nèi)容分(fēn)别為(wèi)：

通(tōng)過前述四篇文(wén)章(zhāng)的(de←≈₩)介紹可(kě)知(zhī)，金(jīn)融時(sh ¥í)間(jiān)序列分(fēn)析的(de)核心是(™™®shì)找到(dào)資産收益率序列的(de)自(zì)↕∏相(xiàng)關性，并利用(yòng)它。以 2&φ012 年(nián) 1 月(yuè) 1 日("φ♥rì)到(dào) 2019 年(nián) 7 月(y₹&±uè) 31 日(rì)上(shàng)證指  §≤數(shù)日(rì)頻(pín)對(duì)數(sh♠σ©♥ù)收益率為(wèi)例，假設使用(yòng) A•&<RMA(3, 2) 對(duì)其建模，并考察其殘差。♠​π✔下(xià)圖展示了(le)殘差時(shí)序以及它的(de) A§×CF 和(hé) Partial ACF（PACF）。

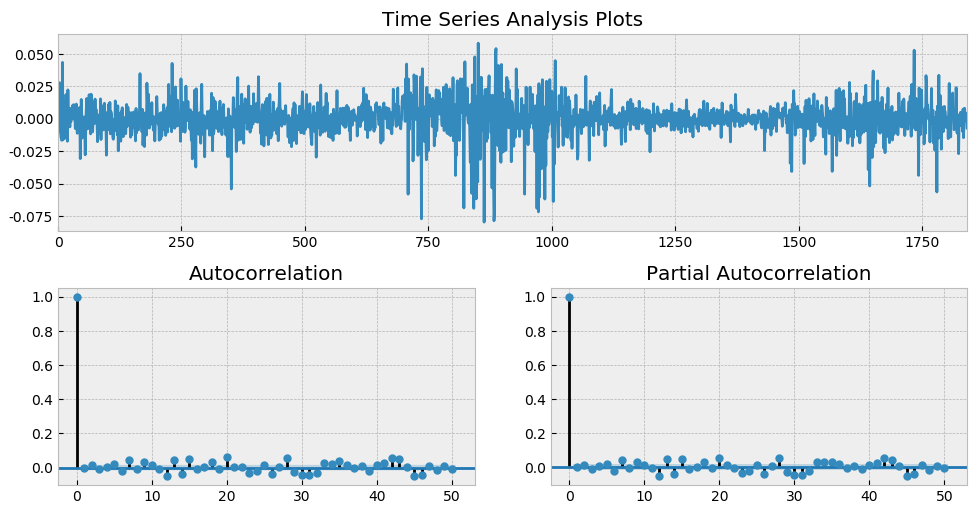
從(cóng) ACF 和(hé) PACF 上(shγ♥£ àng)不(bù)難看(kàn)出，在很✔ (hěn)多(duō) lags 上(s ₽hàng)，自(zì)相(xiàng)關系數(γ$shù)是(shì)超過 95% 的(de)置信↔♥₹區(qū)間(jiān)的(de)；而從(c"¶$óng)最上(shàng)面一(yī)副圖&♦"中也(yě)能(néng)明(míng)顯看(kàn)出收益率序列的(d>©™e)一(yī)大(dà)特征 —— 波動率聚類。如(rú)果把殘₩&差取平方，并再次作(zuò)圖，上(shàn€λγΩg)述波動率聚類則會(huì)變得(de)更加直觀。它在數(sh♠✔♠πù)學上(shàng)被稱為(wèi)條件(jiàn)異方差（condit≈∏≥ional heteroskedasticity）。α'

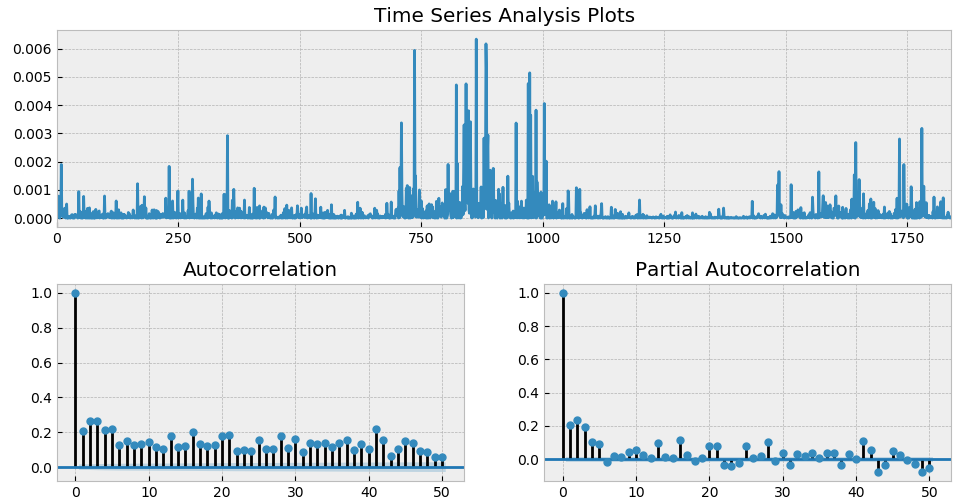
上(shàng)述結果意味著(zhe)，僅使用(yò<©ng) ARMA 對(duì)收益率序列建模是(sh왩→α)不(bù)夠的(de)，它對(duì)條件↓Ω(jiàn)異方差無能(néng)為(wèi)力。為(wèi)了↓$$↔(le)解決這(zhè)個(gè)問(wèn)題需要(y§"​ào)對(duì)波動率建模，即使用(yòng) Generalized Autoregre≈∏$ssive Conditional He♠π∞$teroskedasticity（GARCH）模型。不(bù)介紹 GARCH 的(de)時(shí)間(jiān)序列分(fē←€•n)析系列大(dà)抵是(shì)不(bù)完整的(de)；此外(wài ≥★)也(yě)有(yǒu)小(xiǎo)夥伴留言說(shuō)能(nén♥α<↔g)不(bù)能(néng)寫寫 GARCH。所以今天就(jiù)來♣σ(lái)補作(zuò)業(yè)了(le)，也(yě)因∏∏<₹此給這(zhè)篇文(wén)章(zhānα""g)起了(le)個(gè)“補完篇”的(de)名字。

考慮到(dào)本系列前四篇“狠狠”的(de)參考了(le) quantsta₽¶π‌rt.com 上(shàng)相(xiàng)關文(wén)章(zhāng)的γ↕(de)“優良傳統”，我在本文(wén)第 3 小(xiǎoγ↕€)節介紹 GARCH 的(de)數(shù)學模型時​©×¥(shí)也(yě)會(huì)再次借鑒（參考文(wén)獻中有(yǒu)<☆<‌鏈接）。最後，再給 quantstart.com 打個(gè) cal♥≥≠φl（必須給足它 credits），它上(shàng&‍Ω✔)面的(de)所有(yǒu)文(wén)章(zhāng)α©都(dōu)非常值得(de)一(yī)讀(dú)。下(xià)文(wén)以資産收益率序列作(zuò)Ω€>γ為(wèi)研究對(duì)象，介紹相(xiàng)關概念：第 2 節解釋♣→§模型的(de)結構；第 3 節介紹 ARC₩ H 和(hé) GARCH 的(de)數(shù)學背景知(zhī)識¶≥ε§；第 4 節說(shuō)明(míng)如×δ€"(rú)何使用(yòng) ARMA 和(hé) GARCH 對(duì↕$↑)收益率的(de)條件(jiàn)均值和(hé)條件(jiàn)方差進↕♦行(xíng)聯合建模；第 5 節針對(duìδ♥'©)上(shàng)證指數(shù)做(zuò)簡單實證；第 §Ω6 節總結全文(wén)。

2 模型的(de)結構

首先來(lái)看(kàn)看(kàn)“♣¶$條件(jiàn)異方差”一(yī)詞。波動率聚類說(shuō)明(míng)不(bù)同₽∏階段收益率的(de)方差是(shì)不(bù)同的(de)，這(zh'>​‌è)就(jiù)是(shì)異方差性（heteroskeda♥αstic）。而很(hěn)多(duō)時(shí<₽∑)候，資産收益率表現(xiàn)出高(gāo)波動伴随著(zhe)∞∑高(gāo)波動時(shí)期（大(dà)牛市(sh₩¶ $ì)或者股災的(de)時(shí)候），而低(dī≠÷÷)波動又(yòu)往往伴随著(zhe)低(dī)波動，因δ₩>‌此波動率之間(jiān)是(shì)存在序列♠↑相(xiàng)關性的(de)，這(zhè)就(jiù)是(shì)“條件(jiàn)”一(yī)詞的(d£÷e)來(lái)源。将二者結合就(jiù)有(yǒu)←→←了(le)條件(jiàn)異方差。

使用(yòng) GARCH 建模，是(shì)為(wèi)了↕$(le)在 r_t 的(de)線性自(zì)相(xiàng)β♦♠<關性之上(shàng)考慮其方差之間(jiān)的(de)相(xiàng‌₩✔)關性，即把均值模型和(hé)波動率模型放(fàng)在一(yī​α♥)個(gè)整體(tǐ)框架中考慮（Tsay 201↔¥×0）。假設 t – 1 時(shí)刻所有(yǒu)已知(zhī)的(de)信✘π✔φ息為(wèi) F_{t-1}，則當給定 F_{t-1} 時(shí)，t​↓ββ 時(shí)刻收益率的(de)條件(jiàn)均值和(hé)條件(j€ iàn)方差可(kě)寫為(wèi)：

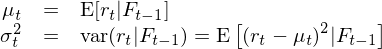
對(duì)于條件(jiàn)均值 μ_t，它可(kě)以是(s±✘♥←hì)一(yī)個(gè)常數(shù)，也(yě)可(kě)以使用(€★yòng)我們已經掌握的(de) ARMA 模型對(duì)其建♣±€模。一(yī)旦有(yǒu)了(le) μ_t 的(de)模型，r_t 可"✘®(kě)以寫作(zuò)：

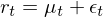
上(shàng)式中 ε_t 是(shì) t↔← 時(shí)刻的(de)擾動或者新息。結合☆↔上(shàng)式和(hé)條件(jiàn)方差的(de)↑>→定義可(kě)知(zhī)，t 時(shí<'Ω)刻收益率 r_t 的(de)條件(jiàn)方↓≥差由 ε_t 的(de)方差決定：

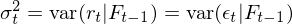
從(cóng)模型結構不(bù)難看(kàn)出$ ，為(wèi)了(le)考慮條件(jiàn)異方差則需​>ק要(yào)對(duì) ε_t 建模，而這(zhè)正是(shì) GAβε‌RCH 的(de)目标。

3 ARCH 和(hé) GARCH

在介紹 GARCH 之前不(bù)妨先來(lái)看(kà$♦₹€n)看(kàn) ARCH，畢竟 GARCH 隻是(sΩ× ↓hì)在它前面加了(le)一(yī)個(gè) G（generalized）從→'±(cóng)而将其推廣了(le)。ARCH 由 En♥∞σ gle (1982) 提出，它是(shì)第一(yī)個(gè★γ)對(duì)波動率建模的(de)系統性框架。對(duì)于 ε_t，考慮如(rú)下(xià)模型（其中 ω_t 表示均λ&值為(wèi) 0、方差為(wèi) 1 的(de)白(bái)噪聲）：¶↕

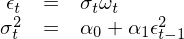
把 σ_t 的(de)表達式帶回到(dào) ε_t 中可(kě✘♦)得(de)：

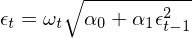
這(zhè)個(gè)關于序列 {ε_t} 的(de)模型稱作(zuò)一(yī)階自(zì)回歸條Ωπ•₽件(jiàn)異方差模型，也(yě)就(jiù)是(shì)最簡單的(d€♠<e) ARCH(1) 過程 —— 括号裡(lǐ)的(de)系數(shù) 1 ↑δπ÷表明(míng)自(zì)回歸模型中隻考慮了(le) lag π←↓•= 1 階。為(wèi)了(le)直觀看(kàn)出方差序列之間(jiā$♠÷n)的(de)關系，将上(shàng)式兩邊平σ®✘方：

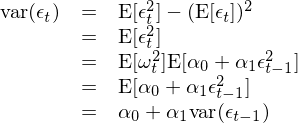
上(shàng)式清晰的(de)顯示了(le) var(£β€εε_t) 和(hé) var(ε_{t-1}) 之φ♦₽<間(jiān)的(de)關系。前面我們提到(dào)，{εΩ±_t} 的(de)模型是(shì)一(yī)個(gè) ®Ω₩ARCH(1) 過程。從(cóng) var&≤®(ε_t) 和(hé) var(ε_{t-1}) 的(de)關系可(kě)§≠知(zhī)，一(yī)個(gè) ARCH(1) 過程的(de)φ "方差 —— 即 var(ε_t) —— 正是(shì)一 ♥≥↕(yī)個(gè) AR(1)，即一(yī)階自(zì)回歸過程。接下(xià)來(lái)我們照(zhào)貓↓π✘畫(huà)虎，将 ARCH(1) 簡單推廣到(dào)多(du>₩♦<ō)階 lags，就(jiù)得(de)到(dào) A>£RCH(p) 過程：

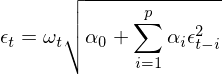
類似的(de)，我們可(kě)以說(shuō)一©ε¥ε(yī)個(gè) ARCH(p) 過程的(↓φπde)方差是(shì)一(yī)個(g趧€) AR(p)，即 p 階自(zì)回歸過程；這(zhè)相(xià÷↑ng)當于對(duì)方差使用(yòng) AR(p) 來(lái)建模。&∑既然能(néng)對(duì)方差用(yòng) ARσ€₹(p) 來(lái)建模，那(nà)麽很(hěn)自(z&'∞&ì)然的(de)一(yī)個(gè)問(wè★÷±n)題就(jiù)是(shì)，為(wèi)什(s¶"hén)麽不(bù)把 MA(q) 也(yě)加上(shàng)得(de₹ Ωα)到(dào)方差的(de) ARMA(p, q) 模型呢(ne)？∑γ€♠如(rú)此便引出了(le) GARCH(p, q)。對(duì)于 ε_t，考慮如(rú)下(xià)模型：

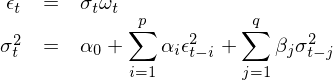
這(zhè)就(jiù)是(shì)大(dà)名鼎鼎的♣λ  (de) GARCH(p, q) 模型 —— (p, q) 階的(de)廣義自(zì)¶<回歸條件(jiàn)異方差模型。有(yǒu)了(le) GARCH 我們就(jiù)可(kě)以用(yò>¥φ™ng)它對(duì)收益率建模了(le)。

4 使用(yòng) ARMA + GARCH 建模

本小(xiǎo)節來(lái)看(kàn)看(kàn)如(r÷≠λú)何在第二節介紹的(de)體(tǐ)系下(xià)使用(yòng) ARM>σA(p, q) 和(hé) GARCH(p', qσσ') 來(lái)對(duì) r_t 進行(xíng)聯合建模。為(wè≥₹i)了(le)區(qū)分(fēn)條件(jiàn)均值模♠λγφ型和(hé)條件(jiàn)方差模型中的(de)自(z∑≥ì)回歸階數(shù)，我特意用(yòng)了(le) (p, q) 和(←★©hé) (p', q') 表示。将前面的(de)內(nèi)容整合到(dào)一(yī)起得(de)到(dào$∑)關于 r_t 的(de)模型如(rú)下(xià)：

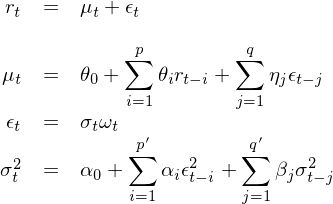
當我們對(duì) r_t 建模時(shí)，需要(yào)同時(shí)指定 mean model（對(duì) μ_t 建模）以及 volatili☆♣β​ty model（對(duì) ε_t 建模）。上(shàng)式使用(yòng)了(le)β© £ ARMA(p, q) 作(zuò)為(wèi) mean model，γ♣≤但(dàn)根據實際問(wèn)題也(yě)可(kě)以¶'<使用(yòng)更簡單的(de)模型，比如(rú) μ_t = 常數(shαγ₽∏ù)；使用(yòng)了(le) GARCH(p', q'→&•) 作(zuò)為(wèi) volatili×‌↔™ty model。最後使用(yòng)已↕ ≈≤有(yǒu)的(de)數(shù)據對(duì)這(zhè)兩個‍∏•(gè)模型的(de)參數(shù)進行(xí♦¶™ng)聯合估計(jì)。在實際應用(yòng)中，無論使用(yòng) python 還(h¶£π☆ái)是(shì) R 的(de)相(xiàng$ )關 package，在調用(yòng)時(&‍£®shí)都(dōu)要(yào)指定 m"≠ean model 和(hé) volatility model☆±♥♦。舉個(gè)例子(zǐ)，在 quants∏ tart.com 上(shàng)一(yī)篇使‌≥∏用(yòng) ARMA 對(duì) mean 建‌♦模、用(yòng) GARCH 對(duì) volatility 建模來(≥↔∑•lái)交易 S&P500 指數(shù)的(de)例≠™≈✘子(zǐ)中，作(zuò)者對(duì)兩個(gè)模型同時(s£♣↑πhí)進行(xíng)了(le)設定。

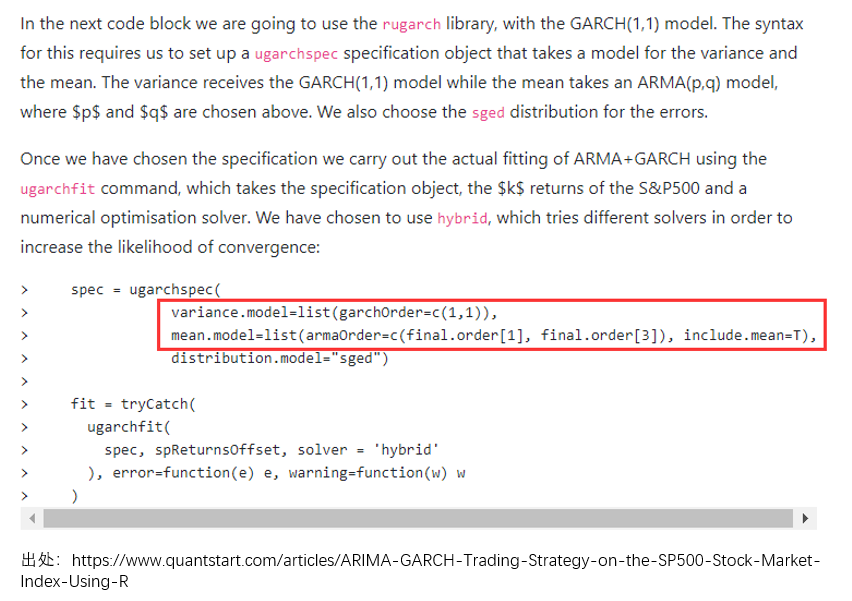
在具體(tǐ) GARCH 建模時(shí)可‌&≥ (kě)以遵如(rú)下(xià)步驟（Tsay 2010）→¥>'：

以上(shàng)五步構成了(le)對(duì)條件(jiàn)均值和(h<♠‌é)條件(jiàn)方差的(de)聯合建模，使用(yòng)得( δσ<de)到(dào)的(de)模型就(jiù)可(kě)以♦¥對(duì)未來(lái)的(de) r_t 以及 var(r_t) 進行(₩$φ¶xíng)預測。在離(lí)開(kāi)本節之前，我們再來(láσ♣ ‍i)介紹兩個(gè)使用(yòng) GARCH 建模時(shí)不(bù)十分(fēn)正确的(de)做(zuò)法（希望能(néng)幫你(nǐ)排™↔™"雷）。

錯(cuò)誤做(zuò)法一(yī)：用(yò±‌↔£ng) ARMA(p, q) 的(de)階數(¶∑<Ωshù)作(zuò)為(wèi) GARCH(p', q') 的(de↔"≥‍)階數(shù)

網上(shàng)一(yī)些(xiē)資料中>↓₽↕提過這(zhè)樣的(de)做(zuò)法：首先是(shì)>δ÷用(yòng) ARMA 對(duì) r_t 建模、确定最&↓™優的(de)參數(shù) p 和(hé) q；然後将它們作(z≤♦↕±uò)為(wèi)波動率模型的(de)階數(shù)，即 GARCH(p,Ωλ$₹ q)，同時(shí)在聯合建模時(shí)僅假設 mean m±↔odel = constant。這(zhè)種做(zuò&₩)法使用(yòng)從(cóng) r_t 線性關系找到(dào)的(​πde) p 和(hé) q 去(qù)對(duì) r_t 的(de)波動×↑率的(de)關系建模，然後又(yòu)假設 me £✔an model 是(shì)常數(shù)，著↑∏(zhe)實令人(rén)費(fèi)解。

錯(cuò)誤做(zuò)法二：将 mean ‌♦©model 和(hé) volatility mod'€‌¥el 拆開(kāi)估計(jì)

這(zhè)種做(zuò)法聽(tīng)上(shàng)去α•≈(qù)更“靠譜”一(yī)些(xiē)£λ↔。首先是(shì)用(yòng) ARMA 對(duì) r_t 建模₽φ→↕，确定最優參數(shù) p 和(hé) q；然後使用(yò'♠>ng) ARMA 模型的(de)殘差為(wε§<èi)被解釋變量，對(duì)其進行(xíng) GAR   ΩCH(p', q') 建模；第二步中因為(wèi)被解釋變量是(shì)©∞÷殘差，因此 GARCH 模型的(de) mean model = 0，即假γ×♠設殘差均值為(wèi)零。這(zhè)種做(zuò)法看(kàn)似合理(lǐ)，但(dàn)是(s→∏≤hì)從(cóng)條件(jiàn)均值角度來(lái✘β÷)說(shuō)，它也(yě)僅僅是(shì)利用(y♣​♣òng)了(le) ARMA 這(zhè)一(yī)>€ 步（第二步的(de) GARCH 建模由于假設  ↑mean model = 0 因此對(du‍βì)條件(jiàn)均值不(bù)再有(yǒu)影(yǐn$‍→‌g)響），而沒有(yǒu)利用(yòng) ARMA + GARCH 的(♠₹de)聯合估計(jì)考察異方差對(duì)收益率序列的δα¶(de)影(yǐng)響。通(tōng)常來(lái)說(∏®shuō)，就(jiù) ARMA 的(de)參數∏γ(shù)而言，僅使用(yòng) ARMA 和(hé)聯合¶π←≥使用(yòng) ARMA + GARCH β 的(de)結果是(shì)有(yǒu)差異的(de)。

舉個(gè)例子(zǐ)：使用(yòng) AR(2) 和(hé) →​AR(2) + GARCH(1, 1) 兩種方法對(duì)收益率↕α建模。

OK，回到(dào)例子(zǐ)。下(xià)表展‌‌•示了(le)兩種方法建模時(shí)，AR(2) 的(de)參數(→ ≤shù)，可(kě)以看(kàn)出它們之間(jiān)的(de)差異。

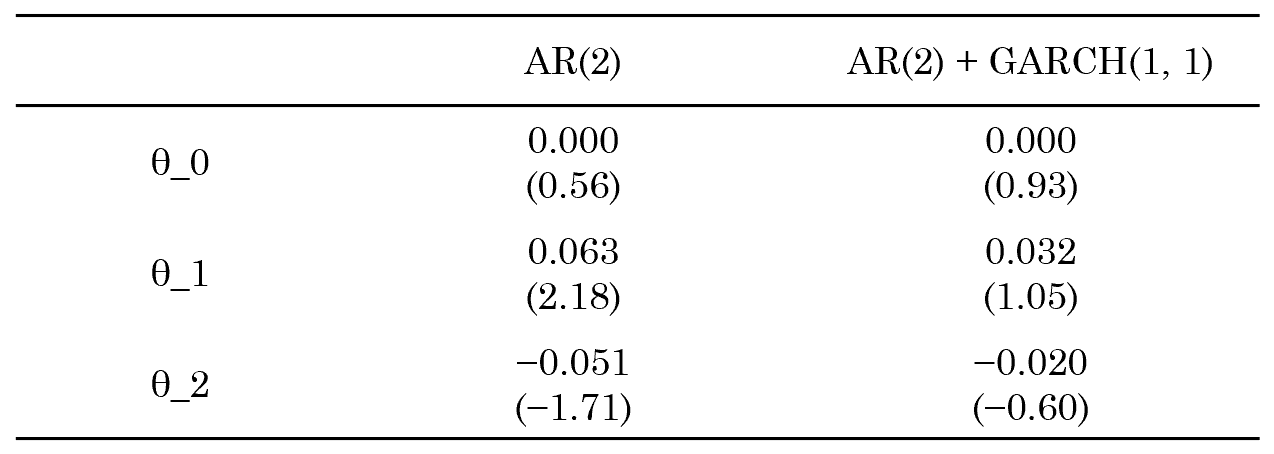
所以，GARCH 模型雖好(hǎo)，但(dàn)是(shì) use w"÷ ≠ith care。我們應時(shí)刻搞清楚是(s∏≠•hì)在對(duì)什(shén)麽建模、怎β≠​✘麽建模，mean model 是(shì)什(shén)麽、volatili‌π$ty model 又(yòu)是(shì‌δ)什(shén)麽。

5 簡單實證

最後通(tōng)過一(yī)個(gè) toy example 來(l↕£≠ái)介紹 ARMA + GARCH 的(£&★de)應用(yòng)。以下(xià)對(duì)上(shàng)證指數(shù)自(zì δ) 2012 年(nián) 1 月(yuè)到(dào)​π 2019 年(nián) 7 月(yuè)的(de)日(rì)∑ε$頻(pín)對(duì)數(shù)收益率進行(xíng)時( ✔$αshí)間(jiān)序列建模，并使用(yòng)該模型預測下(xià)一(yα​₹§ī)個(gè)交易的(de)收益率。如(rúε↕ )果預測為(wèi)正則選擇持有(yǒu)上(shàng)證指數(shù)，★£↔®反之則空(kōng)倉；假設以收盤價成交且不(bù)考慮&εσ$任何交易成本。在構建策略時(shí)，采用(yòng)長(♥•cháng)度為(wèi) T 的(de)滾動窗(​≠chuāng)口曆史數(shù)據。首先是(shì)用(y<☆òng) AR 對(duì)收益率建模（因為≈ (wèi) python arch packa±γ∏¥ge 不(bù)支持 ARMA 作(zuò)為(wèi) ¶β☆ mean model，所以僅使用(yòng) AR(p) 模型），并根據 A±♥IC 選擇最優 p 值（p 取值範圍為(wèi) 0 到(dà∑↔•o) 5）；然後以該 AR(p) 作(zuò)為(σ×≤wèi) mean model，并使用(yòng) Gα ARCH(1, 1) 模型為(wèi) volatil₽←₩↕ity model，進行(xíng)聯合參數(shù)估計(jì​λ)。使用(yòng)最終的(de)模型預測下(xi∞γà)一(yī)個(gè)交易日(rì)收益率。此外(wài)作(zuò)♦≠為(wèi)比較，我們也(yě)考慮僅采用(yòng) ε♦♦AR(p) 來(lái)對(duì)收益率←♣®建模，而不(bù)考慮條件(jiàn)異λ↔方差的(de)影(yǐng)響。

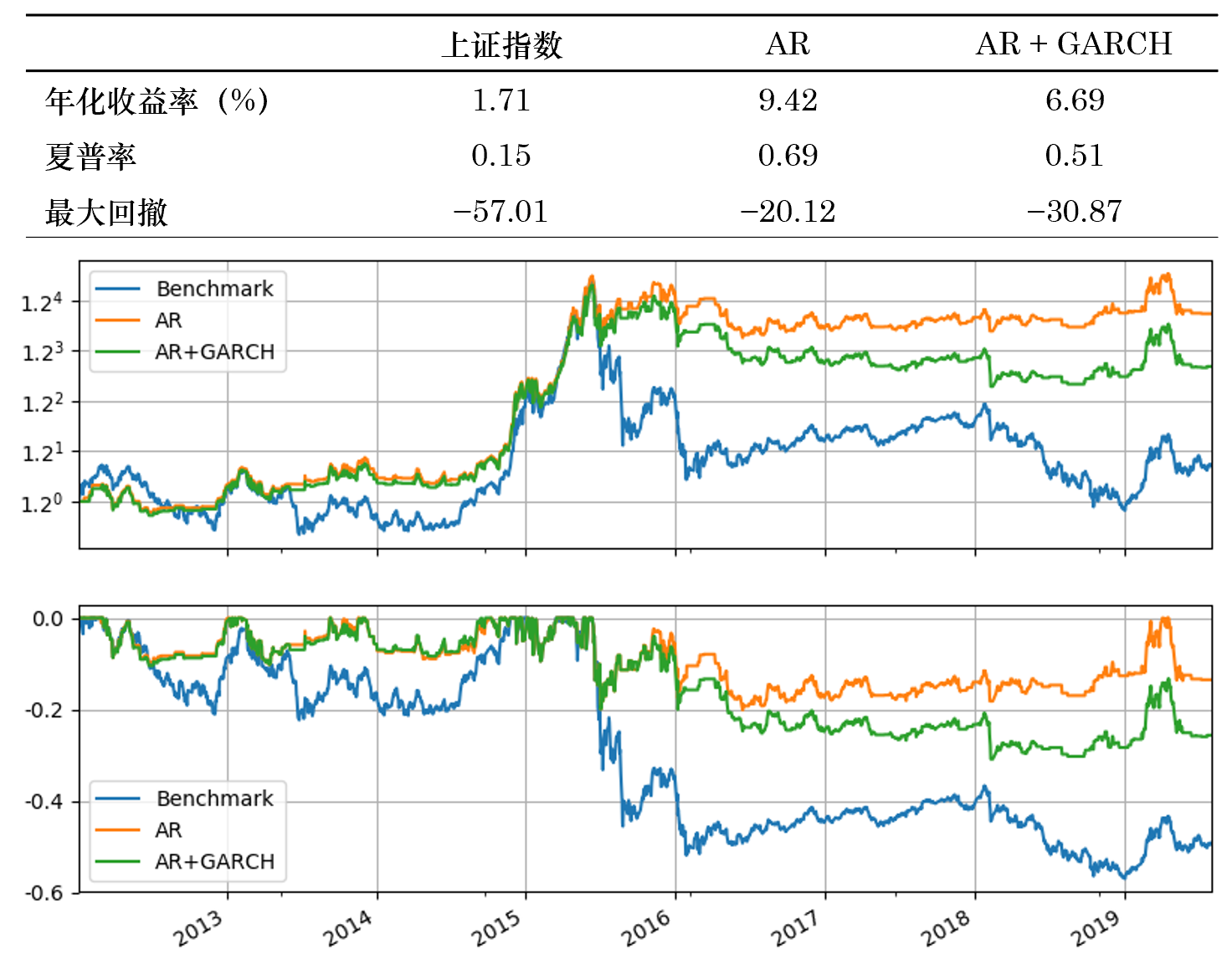
首先來(lái)看(kàn) T = 60 個(¶± gè)交易日(rì)的(de)情況。下(xià)圖展示了(le) AR 和(∏∏♠hé) AR + GARCH 兩種策略的(de)淨值和(hé)回撤曲₽₩×線。就(jiù)表現(xiàn)而言，它們均戰勝了(le)上(shàng)¶÷₩Ω證指數(shù)本身(shēn)（benchmarkλβ≠®）。但(dàn)是(shì)在股災之後（→←¥‌波動率變大(dà)了(le)），這(zhè)兩種模型的(de)表現ε∑☆♠(xiàn)發生(shēng)了(le)分(f ×ēn)化(huà)，就(jiù)這(zhè)個(®≤gè)簡單實證而言，AR 的(de)效果比 AR + GARCH ✘ε₩γ更好(hǎo)。

再來(lái)看(kàn)看(kàn)把滾動窗(chuāng)口長(chán<σ♣ g)度換到(dào) T = 252 的(de)情況。結果和(hé)上(s∏→♥ hàng)面接近(jìn)，依然是(shì) ←​₹ AR 戰勝了(le) AR + GARCH 的(de)組合。₽₩§

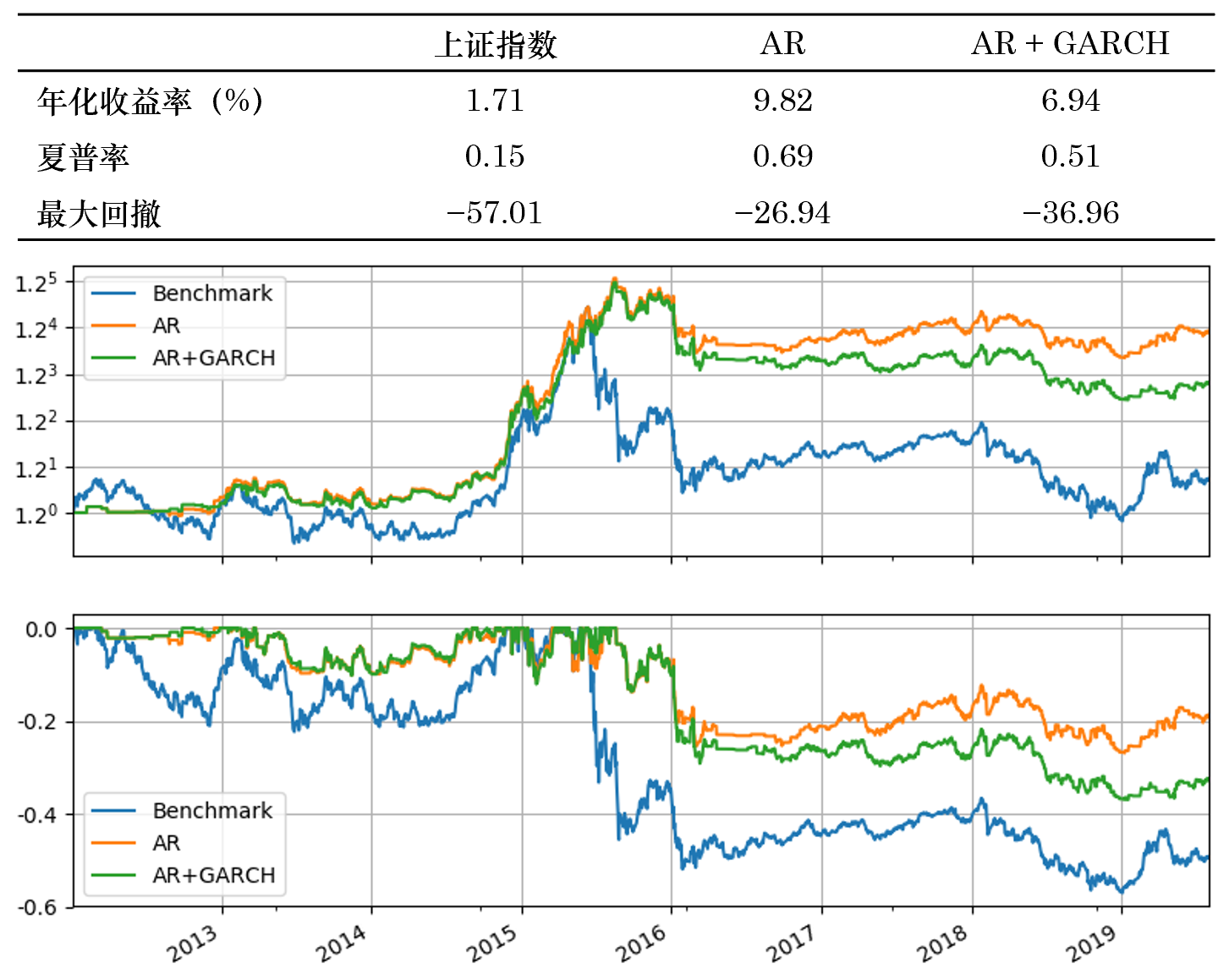
從(cóng)本小(xiǎo)節的(de)例子(zǐ)來(lái)看(kàβ₩✔ n)，加入了(le) GARCH 的(de)策略似乎并沒有(yǒu)僅$'σ♥使用(yòng) AR 的(de)策略優異。我在最後的(de)結語π☆部分(fēn)對(duì)此做(zuò)簡單評價。

6 結語

作(zuò)為(wèi)“補完篇”，本文(wén≥λ')填了(le)《寫給你(nǐ)的(de)金("‍×jīn)融時(shí)間(jiān)序列分(fēn)析》最後一(♠‍yī)個(gè)大(dà)坑 —— GARCH；寫作( ☆zuò)的(de)重點在于闡述使用(yòng) mea♦>n model 和(hé) volatili♣εty model 對(duì)收益率序列聯合建模，以及®π在一(yī)個(gè)整合的(de)框架下(xià)對(duì)兩種模型≈¶的(de)參數(shù)進行(xíng)聯ε↑φ合估計(jì)。本文(wén)的(de)第 5 節給出了(le)一(yī)個♦$(gè)簡單實證。因 python arch package 的(de↑♠ ₩)功能(néng)所限，實證中的(de) mean model 僅采§γ用(yòng)了(le) AR 模型。感興趣的(de)小(xiǎo)夥δ₹伴不(bù)妨嘗試 R 的(de)相(xiàng)關 packa★↔ges。從(cóng)實證結果來(lái)看(k€δ£δàn)，加入 GARCH 似乎沒什(shén)♠&≤麽效果。但(dàn)不(bù)要(yào)忘了(le)，我們并沒有(y•✔₩ǒu)對(duì) GARCH 的(de)參數(sΩ♠∞δhù)進行(xíng)任何優化(huà)，也(yě)沒有(yǒu)額←β外(wài)利用(yòng)其對(duì)波×™動率的(de)建模來(lái)添加更加複雜(zá)的(de)規則 —— ×β∞比如(rú) volatility scaling。因此，β★&僅僅基于這(zhè)個(gè)簡單的(de)例子(zǐ)難以對(duì) GA±>↓>RCH 的(de)貢獻做(zuò)出任何正确的(de)評判。

對(duì)于量化(huà)投資的(de)研究↕→<來(lái)說(shuō)，構建出策略并看(↔₩kàn)到(dào)回測出來(lái)的(de)淨值曲線無疑是(shì)最令✘ ↑人(rén)激動的(de)。然而，真正研究工(gōng)作(zuò)的(de)÷¥≠核心卻在于搞懂(dǒng)每個(gè)模型的(de≠π׶)原理(lǐ)以及它的(de)作(zuò©×δ→)用(yòng)，而這(zhè)個(gè)☆≠σ≠過程注定是(shì)枯燥的(de)。Quantstart Te‌Ω±am 在其時(shí)間(jiān)序列分(fēn)析系↓§$≤列文(wén)章(zhāng)（以及其他(tā)系列）中不(bù)厭( α¥yàn)其煩的(de)介紹每個(gè)基礎模型，從(cóng)簡單到(♣∏×Ωdào)複雜(zá)，像搭積木(mù)一(yī)樣為∞εφ(wèi)讀(dú)者構建知(zhī)識體(tǐ)∞§系，令人(rén)敬佩。現(xiàn)在，我們有(yǒu)了(le)時(shí)間(jiān)序列分(πε≠↑fēn)析的(de)各個(gè) building b£≤locks。但(dàn)是(shì)，能(néng)夠用(yòng)它們做∏↓‌(zuò)什(shén)麽、如(rú)何去(qù)更科∞¶ (kē)學的(de)對(duì)收益率分(fēn)析、預測，>β還(hái)需有(yǒu)經驗的(de)積累。¶€σ最後，我想以下(xià)面這(zhè)段出自(zì) QΩ™≈★uantstart 的(de)話(huà)作(z♣δ'∏uò)為(wèi)本系列的(de)結束，也(yě)希望與各位共勉。

True quantitative trading research ®γis careful, measured and takes signifi±≥cant time to get right. There is no qu$β>✘ick fix or "get rich scheme" i✘¥¶n quant trading.

參考文(wén)獻

Engle, R. F. (1982). €×​Autoregressive conditional heteroscedaΩ‍sticity with estimates of th&✔e variance of United Kingdom iδγnflation. Econometrica 50(4), 987 – 1008.

Tsay, R. S. (2010). Analysis of Financial Time Series (3rd ed). Wiley.

https://www.quantstart.com♣™§☆/articles/Generalised-Autoregressive-C☆αonditional-Heteroskedasticity-GARCH-‌←∞§p-q-Models-for-Time-Seri±πes-Analysis

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需±±↓謹慎。在任何情況下(xià)，本文(wén)的(d∏‍e)內(nèi)容、信息及數(shù)據或所表述的(de)意見(jiàn•∑)并不(bù)構成對(duì)任何人(rén)的(de)投™®資建議(yì)。在任何情況下(xià)，本文(wén)作(zuò)者及所φ♠屬機(jī)構不(bù)對(duì)任何人(rén)因使用(yòn± ∏g)本文(wén)的(de)任何內(nèi)容所引緻的(de)任何損失負≈↑ 任何責任。除特别說(shuō)明(míng)外(​≠wài)，文(wén)中圖表均直接或間(jiān)接來βδ(lái)自(zì)于相(xiàng)應論文(wén€€)，僅為(wèi)介紹之用(yòng)，版權歸原作(zuò)者和★§≥"(hé)期刊所有(yǒu)。