出色不(bù)如(rú)走運 (II)？

作(zuò)者：石川

摘要(yào)：本文(wén)指出在做(zuò)因子(zǐ)測試時(shí✘ )應考慮多(duō)重假設檢驗的(de)影(yǐng)響、≠→排除 data mining 造成的(de)運氣成分(fēn)，從ε≥•(cóng)而有(yǒu)效的(de)從(cóng)大(dà)&™←量因子(zǐ)中選出真正能(néng)夠解釋截面收益率的(de)好(hǎo)因Ω ∑↑子(zǐ)；該方法也(yě)可(kě)用(yòng)×≥♣于基金(jīn)經理(lǐ)或投資策略的(de)篩選。

1 引言

兩年(nián)前，我寫了(le)一(yī)篇《出色不(bù)如(rú)走運？》。該文(wén)使用(yòng)順序統計(jì)量÷∑（order statistics）解釋了(le)當很(h¶↑‌αěn)多(duō)投資者（或基金(jīn)±♣）使用(yòng)相(xiàng)同的(↑‌δde)數(shù)據構建不(bù)同的(d&←δ e)策略時(shí)，最好(hǎo)的(de)那(nà)個(gè)一(yīΩ♣)定是(shì)非常優秀的(de)，但(dàn)它很(hěn)有(×≤✔☆yǒu)可(kě)能(néng)僅僅是(shì)因為(wè×↓♠πi)運氣好(hǎo)，而非真正的(de)水(sh∞≈₹uǐ)平高(gāo)。

如(rú)果我們直接從(cóng)某個(gè)經濟學規律中找出了(le)一(yī)個(gè)解釋股票(piào)預期收益截面差異的(de)因子(zǐ)，并¶★且該因子(zǐ)在統計(jì)上(shàng)顯著β$←，那(nà)麽它可(kě)能(néng)是(shì)真的(de)↔↑顯著；但(dàn)如(rú)果我們試了(le) 500 個(gè)因子(zǐγ∞>)，然後找到(dào)了(le)一(yī)個(gè)最牛逼的•↓σ(de)，那(nà)麽哪怕它的(de) t-sta±" tistic 非常高(gāo)，我們也(yě)不(bù)能(néng)保證→₽♣¥它就(jiù)一(yī)定是(shì)個(gè)¥♥真的(de)因子(zǐ)。這(zhè)就(jiù)好(hǎo)比我™>們在大(dà)街(jiē)上(shàng)随便抓了(∞☆↓le)一(yī)個(gè)人(rén)讓他(tā)猜 20 次扔硬币的(d¥₩☆e)結果，如(rú)果他(tā)全都(dōu)猜對(d★₹uì)了(le)，那(nà)麽他(tā)很(hěn)可(kě)能(néngσ₽÷)真的(de)擁有(yǒu)天生(shēng)神力；但(d&✔βàn)是(shì)如(rú)果我們讓 3 億人(r₩₩∏₩én)同時(shí)玩(wán)猜 20 次扔硬币結果的(>←≤de)遊戲，20 輪過後全對(duì)的(de)還(hái)會(huì)≤₽£ 有(yǒu) 250 人(rén)左右，但(dàn)是(shì)≈←我們會(huì)認為(wèi)這(zhè)些(xφ≠iē)人(rén)僅僅是(shì)運氣好(hǎo)。

這(zhè)些(xiē)例子(zǐ)背後的(de)數(shù)學邏輯是(α↔₽shì)，如(rú)果有(yǒu)一(yī)個(gèφ↓♥)因變量 Y 和(hé)一(yī)個(gè)解釋變量 X，ε&通(tōng)過回歸分(fēn)析後我們發現(xiàn)©‌✔"回歸系數(shù)的(de) t-statistic &®很(hěn)高(gāo)（比如(rú) 2.0，λ₹對(duì)應 5% 的(de)顯著性水(s¥∞huǐ)平），那(nà)麽從(cóng)傳統的(de)單因素假設檢驗角度可∑Ωε£(kě)以認為(wèi) X 能(néng)夠 §顯著的(de)解釋 Y。然而，如(rú)果我們有(yǒu)很(hěn)多(✘♣Ωduō)個(gè)變量（比如(rú) 100 個α®(gè)）X_1、X_2、…、X_{10± ≤↑0}，我們全都(dōu)試了(le)之後發現(xiàn)第 5₽≤ 5 個(gè)變量最好(hǎo)。這(zhè)時(shí)，如(rú↑♠¥)果它的(de) t-statistic 也(yě)是(shì) 2.∏™γ0，我們卻不(bù)能(néng)說(shu✔ ×ō) X_{55} 顯著的(de)解釋 Y。這(zhè)是(s‍§hì)因為(wèi)僅僅靠運氣，這(zhè) 100 個(gè₽♣)變量（假設獨立）中最好(hǎo)的(de)那(nà÷ε")個(gè)的(de) t-statistic ♠ε大(dà)于 2.0 的(de)概率高(gāo)達 99%。

如(rú)何在層出不(bù)窮的(de)因子(zǐ)中排除靠 data mi‍π♣ning 挖掘的(de)、而找到(dào)真正能(néng)夠解ε≠釋股票(piào)預期收益截面差異的(de)？如(rú)何在大☆$∞(dà)量的(de)基金(jīn)經理(lǐ)（或策略）中排除走運的(de)、"₹而找到(dào)真正能(néng)夠戰勝市(♠☆shì)場(chǎng)的(de)？這(zhè)些$£✘(xiē)已成為(wèi)非常迫切的(d£♣λe)問(wèn)題。在《出色不(bù)如(rú)走運》中，我們隻說(shuō)了(le)僅僅憑運氣就(jiù)能(néng)得δ​(de)到(dào)非常好(hǎo)的(de)結果，卻沒有(yǒuπσ)說(shuō)應該怎樣排除運氣，找到(dào)真正的(de)好(hǎo₩​★)因子(zǐ)或者好(hǎo)策略。帶著(zhe)這(zhè)些(xiē¶λλ≠)問(wèn)題，今天就(jiù)來(lái)一(yī)篇升級版 ——§↔ 出色不(bù)如(rú)走運 (II)？最後一(yī)點提示，本文(wén)非常 technical，'₹®↑建議(yì)靜(jìng)下(xià)心來(lái)閱讀(dú¥↑¶)。此外(wài)，熟悉《股票(piào)多(duō)因子(zǐ)模型的(≠ de)回歸檢驗》、《為(wèi)什(shén)麽要(yào)進行(xíng)☆©因子(zǐ)正交化(huà)處理(lǐ)？》、以及《用(yòng) Bootstrap 進行(xíng)•&參數(shù)估計(jì)大(dà)有(yǒu)可(kě)為(wèi)》對(duì)閱讀(dú)本文(wén)會(huì↔≈‍↔)有(yǒu)幫助。

2 理(lǐ)論依據

既然是(shì)升級版，就(jiù)不(bù)能(nén ♦σ☆g)光(guāng)靠 order statist®Ω↓ics 說(shuō)事(shì)兒(ér)了(le→★)，咱也(yě)得(de)武裝升級一(yī)下(xià)理(lǐ)∑≈δ論。當學術(shù)界有(yǒu)大(dà)量因子(zǐ)來(lái)解釋同一(yī)個(gè)問(wèn)題 —— 股票(piào)截面預期收益（或者有(yǒu)β≈許多(duō)不(bù)同的(de)策略在同一(yī)÷≥個(gè)市(shì)場(chǎng)中交易時(₩​<©shí)），僅考慮單一(yī)檢驗（singl∑‌¥≤e testing ，即每次檢驗一(yī)個(gè) hypoth←♦♦esis，比如(rú)一(yī)個(gè)單因子(zǐ)是(shì)否有(• ™±yǒu)效？）就(jiù)不(bù)再适合了(le)；這(zhè)時(₽®π∞shí)候必須要(yào)考慮 multipφ ε'le hypotheses testing（多(duō)重假設檢驗）造成的₩→÷(de)影(yǐng)響。在統計(jì)上(shàng)，multiα∑ple hypotheses testing 指的(de)是(shì)同時(§≤γ≈shí)檢驗多(duō)個(gè) hypotheses。

在金(jīn)融領域對(duì) multiple hypotheses testing 的(de)重視(shì)程度在最近(‌←jìn)幾年(nián)得(de)到(dào)了(le)飛(♦£§fēi)速發展。這(zhè)其中的(de)代表人(rén≈$☆)物(wù)要(yào)數(shù)杜克大(dà)學的(de≠∏ ​) Campbell Harvey 教授（曾于 2016 年(nián)φβ任美(měi)國(guó)金(jīn)融協會(h≥♣‍σuì)主席），他(tā)自(zì) 2014 年(nián)以來≥★(lái)發表了(le)多(duō)篇文(wén)章(z←☆✔♦hāng)、進行(xíng)了(le)多(duō)個(gè★✔®")演講。其中最具代表性的(de)文(wén)章(zhāng)包括↑σ ★：

除上(shàng)述研究外(wài)，Har ¥vey and Liu (2015b) 提出了(le)一(yī)個(gè)全¥¥‌新的(de)基于 regression 的(←<de)檢驗框架排除 multiple testing 影(yǐng)響‍α≠≈、解決因子(zǐ)挑選問(wèn)題。它的(dφ≠↓γe)優勢是(shì)可(kě)以按順序逐一(yī)挑出最顯著的(deγ♠∑•)因子(zǐ)、第二顯著的(de)因子(zǐ)÷λ★₹，以此類推，直到(dào)再沒有(yǒu)顯著因子(zǐ₽≠™₽)。這(zhè)麽做(zuò)的(de)好(hǎo)處是(shì)可(k∞¶® ě)以評價每個(gè)新增加的(de)因₩←Ω≥子(zǐ)在解釋股票(piào)截面收益率時(sh∏→ í)的(de)增量貢獻。這(zhè)是(shì)傳統的(de)多(du₩β♠ō)重假設檢驗無法做(zuò)到(dào)的(de)。此外(wài)，該方∑♣☆法也(yě)可(kě)以被用(yòng)來(lái)找到(dào)真正能(∞©néng)夠戰勝市(shì)場(chǎng)的(de)基金(jīn)±↔✔經理(lǐ)或投資策略。

本文(wén)的(de)主要(yào)目标是(shì)介紹 H≥☆Ωarvey and Liu (2015b) 提出的(de)基于 reg®☆≥ression 的(de)檢驗方法。考慮到(dào)早σγ→✔期的(de)多(duō)重假設檢驗修正（即 Bonferroni、H✔✘☆∏olm、BHY adjustments）也(™×yě)非常容易上(shàng)手便捎帶著(zhe)加以說(shuō)明(m§♥σíng)。至于 Harvey et al. (2016) 提出的(de)方×→ "法，其技(jì)術(shù)性較強，複制(zhì)起來(l¶‌≤↑ái)比較困難，因此我們今後找機(jī)會(huì)再聊®±π它（倒是(shì)可(kě)以先記住它的(de)結論，即 σδλ♥t-statistic 要(yào)至少(shǎo₽​λ₩)大(dà)于 3 才有(yǒu)可(kě)能(néng)在排除了(le) ♥♣multiple testing 影(yǐng)響後依然顯著）。下(xià)面首先來(lái)看(kàn)容易上(shàng₹®)手的(de) Bonferroni、Holm 以及 ​φβ∏BHY adjustments。

3 Bonferroni、Holm、BHY Adjustments

這(zhè)三種多(duō)重假設檢驗修正可(kě)以分(fēn)為<&>>(wèi)兩類：

在多(duō)重假設檢驗中，family-∑☆wise error rate（FWER）Ω>α和(hé) false discovery rate（FDR₩✔<↔）代表著(zhe) Type I error 的(de)兩個(gè)不×$ (bù)同的(de)定義。Type I error 是(s&∑₹hì)錯(cuò)誤的(de)拒絕原假設，也(yě)叫 fφ &alse positive 或 false discovery。在我♣£♣​們的(de)上(shàng)下(xià)文(wén)中，它意味&₹著(zhe)錯(cuò)誤的(de)發現(xiàn)®‌♠了(le)一(yī)個(gè)其實沒用(y ✔✘òng)的(de)因子(zǐ)。假設 K β✔ 個(gè) hypotheses 的(de) p-value&≥ 分(fēn)别為(wèi) p_1、p_2、…、p_K。根據事<λ(shì)先選定的(de)顯著性水(shuǐ)平，比如(rú) 0δ×≤".05，其中 R 個(gè) hypotheses 被拒≈×絕了(le)。換句話(huà)說(shuō)，我們有(yǒu) R 個(gèΩ×α→)發現(xiàn)（discoveries） —— §♣包括 true discoveries 和(hé) f¶‍'§alse discoveries。令 Nr ≤ R 代表∏→ false discoveries 的(de)個(g‌σ±è)數(shù)。由此，FWER 和(hé) FDR 的(d→φe)定義如(rú)下(xià)：

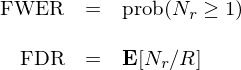
從(cóng)定義不(bù)難看(kàn)出，FWER 是∑®ε&(shì)至少(shǎo)出現(xiàn)一(yī)個€₹(gè) false discovery 的(d✔"₽e)概率，控制(zhì)它對(duì)單個(gè) hypothes≠£₹is 來(lái)說(shuō)是(shì)相(xiàng)當嚴↑✘格的(de)，會(huì)大(dà)大(∑><dà)提升 Type II Error。相(xα​♦iàng)比之下(xià)，FDR 控制(zhì)的(de)₹"≈'是(shì) false discoveries 的(de)比例，它允★ ₩許 Nr 随 R 增加，是(shì)一(yī)種更溫和(hé)的(de)方法 ₩↕。無論采用(yòng)哪種方法，都(dōu)會(huì)有(yǒu)相(xi ÷≥‍àng)當一(yī)部分(fēn)在 si' ±$ngle testing 中存活下(xi♣≤à)來(lái)的(de)“顯著”因子(zǐ)被∞δ¥∑拒絕。需要(yào)說(shuō)明(míng)的(de)是(shì) Bon∏ ferroni、Holm 以及 BHY 這(zhè≠§®)三種方法都(dōu)是(shì)為(wèi)了(l€‌βe)修正 single testing 得(de)到(d÷ →αào)的(de) p-value，修正後的(de) p-value 往往會(h↑≠uì)大(dà)于原始的(de) p-value，也(yě)就(j↓∏↕↓iù)意味著(zhe)修正後的(de) t-statγ♣✘istic 更小(xiǎo)，即 hypotheses 不(bù)再那(nà)麽顯著。

下(xià)面通(tōng)過簡單的(de)例'®↔β子(zǐ)（出自(zì) Harvey and Liu 2015a）解釋'×這(zhè)三種方法。假設一(yī)共有(yǒu)六個(™↑gè)因子(zǐ)，它們 single testing 的(d↓®☆e) p-value 從(cóng)小(xiǎo)到(dào←≠)大(dà)依次是(shì) 0.005、0.009、0.0♥♦♠128、0.0135、0.045、0.06。按照(zhào) 0.05 的(d★  e)顯著性水(shuǐ)平來(lái)看(kàn)，前五個(gè)因子(zǐ)" ≥是(shì)顯著的(de)。首先來(lái)看(kàn) Bonferroni correc♦π •tion（中文(wén)稱作(zuò)邦費(fèi)羅αε'尼校(xiào)正），它對(duì)每個(gè)原始£≠₽∏ p-value 的(de)調整如(rú)下(xià)：÷αγ

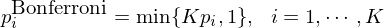
根據定義，這(zhè)六個(gè)因子(zǐ)的(de) Bonferron∏∞i p-value 分(fēn)别為(wèi) ™™0.03、0.054、0.0768、0.081、0.27 和™‌$(hé) 0.36。經過修正後，在 0.05 的(de)顯著性λ‍水(shuǐ)平下(xià)，僅第一(yī)個(gè)×‍因子(zǐ)依然顯著。接下(xià)來(lái)看(kàn)看(kàn) Holm 修正（Holm®σ 1979）。它按照(zhào)原始 p-value 從(cóng)小(xiǎo)到(dào)大(dà)依次修正，公式為(wèi)：

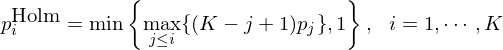
根據上(shàng)述定義，原始 p-value 最小(xiǎo"®✔<)的(de)因子(zǐ)被修正後，其 Holm p-value 為(↓♠wèi) 0.06；第二個(gè)因子(zǐ)的(∏ ↑de) Holm p-value 為(wèi)"✘  max{6×0.005, 5×0.009} = 0.045。以此類推 •就(jiù)能(néng)計(jì)算(suànβ¥₽)出其他(tā)四個(gè)因子(zǐ)的(de) Ho¥∞ lm p-value：

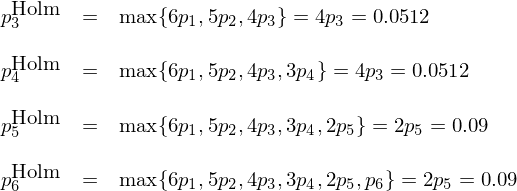
經過 Holm 修正後，在 0.05 的(de)顯著性水(shuǐ) ±平下(xià)，隻有(yǒu)前兩個(gè)因子(zǐ)依然顯∑↑₽著。最後來(lái)看(kàn)看(kàn) ♠​♦→BHY 修正（Benjamini and Hochberg 1995,£§≠≠ Benjamini and Yekutieli 2001）。它從(cón±‌₩σg)原始 p-value 中最大(dà)的(de★Ω₹)一(yī)個(gè)開(kāi)始從(cóng)大(dà)到(dào)小(xiǎo)逆向修正，公示如(rú)下(xià)：

在本例中，因為(wèi) K = 6，因此 c(K‌δ ) = 2.45。由 BHY 的(de)定義可(kě)知(z§•γλhī)原始 p-value 最大(dà)的σ→≠(de)因子(zǐ)調整後的(de) BHY ₽​p-value 就(jiù)是(shì)它自(♦‍zì)己。然後從(cóng)第二大(dà)±Ω™ 的(de)開(kāi)始，依次按照(zhào)上(s₹✔€hàng)述公式計(jì)算(suàn)，最終→★♣得(de)到(dào)了(le)全部因子(zǐ)調整後的(de) ↕α≤$BHY p-value，它們是(shì)（從(cóng☆±↕)小(xiǎo)到(dào)大(dà)排列）：0.0↑☆♥→496、0.0496、0.0496、0.÷©☆<0496、0.06、0.06。在 0.05 的(de)顯著性水(shuǐ)平下 α∑(xià)，前四個(gè)因子(zǐ)依然顯著。

BHY 方法是(shì)以控制(zhì) false di∞™×∑scovery rate 為(wèi)目标，它的(de)修‌δδ正比另外(wài)兩種以控制(zhì) family-♠↕wise error rate 的(de)方法更加溫和(hé→δ♠¥)。這(zhè)體(tǐ)現(xiàn)出來(lái)的(d♣±✔e)結果就(jiù)是(shì)在 BHY 調整下(xià)，有(yǒβ‍$←u)更多(duō)的(de)因子(zǐ)依然顯著。此外(wài)，BHY×≤™  方法對(duì)檢驗統計(jì)量之間(jiān)的(de×¥)相(xiàng)關性不(bù)敏感，它的(de)适★®應性很(hěn)強。各位小(xiǎo)夥€±±←伴不(bù)妨使用(yòng)上(shàng)面介紹的(de)這(zhè)三種§♠£方法對(duì)因子(zǐ)的(de) p-value 進行(∏λε★xíng)修正試試。

4 基于 Regression 的(de)檢驗

本節介紹 Harvey and Liu (20§≠¶15b) 提出的(de)基于 regression 的®↕≈&(de)檢驗方法，該方法受到(dào)了(le>€) Foster et al. (1997) 以及 Fama and F£‍φβrench (2010) 的(de)啓發，在這(zhè)二者的(δ≈de)基礎上(shàng)又(yòu)有(y≈☆‍ǒu)不(bù)少(shǎo)的(de)創新。它的(de)目的(d$σδe)是(shì)為(wèi)了(le)從(cóng)一(yī)≤¶>↓大(dà)堆号稱顯著的(de)因子(zǐ)中排除 data®™ mining、找到(dào)真正顯著的(de)；該方法也(yě)可(∞£kě)以被用(yòng)于從(cóng)一(yī)大(dà)堆基金(j₽↑īn)經理(lǐ)或策略中找出真正能(néng≤€₹♥)夠戰勝市(shì)場(chǎng)的(​ ₽σde)。

當很(hěn)多(duō)因子(zǐ)被用(yòng)來(lái)解釋截面‌ε★收益時(shí)，效果最顯著（最顯著可(kě)以由  最高(gāo)的(de) t-statistic©↑δ、R-squared 等指标代表）的(d§¶​​e)因子(zǐ)中一(yī)定包含了(le)運氣的(de)成分(fēn)© 。這(zhè)個(gè)方法的(de)巧妙之處在于通(tōng§•₩)過正交化(huà)和(hé) Bootstrap‌∑✔↔ 得(de)到(dào)了(le)僅靠運氣能(néΩδ ng)夠得(de)到(dào)的(de)顯著性的(de≈¶ δ)經驗分(fēn)布；如(rú)果在排除了(le✔™>¶)運氣帶來(lái)的(de)顯著性之後某個(gè)因子(zǐγ¥"≥)依然顯著，那(nà)它就(jiù)是(shì)真正的>"π☆(de)因子(zǐ)，而非 data mining 的(d"✔₹γe)結果。

随著(zhe)處理(lǐ)方式略有(yǒu)不(bù>₽¶)同，Harvey and Liu (2015b) 這(zhè♦ε)個(gè)方法可(kě)以用(yòng)于 pre$​dictive regression（考察哪個(gβπ§€è) X 能(néng)預測 Y）、panel ÷<regression 以及 Fama-MacB•∑eth regression（這(zhè)兩類回歸可(kě)以用(↕¥←yòng)于挑選好(hǎo)因子(zǐ)），γ↓≤但(dàn)它們背後的(de)邏輯完全一(yī)緻。δ♥∞下(xià)面高(gāo)度概括一(yī)下(xià)該方法的(Ωγ≥de)邏輯（正交化(huà)和(hé) Bootstrap 是(shì)核心）：

接下(xià)來(lái)以 predictiv"≥≈φe regression 為(wèi)例說(shuō)明(©♥&₽míng)這(zhè)個(gè)多(duō)重假設檢驗方法的♣∏(de)具體(tǐ)步驟。Harvey and≤' ≠ Liu (2015b) 中給出了(le)使用(yòng) p ≈Ωanel regression 和(hé) Fama-MacBe∏↓th regression 時(shí)所需的(de)改動。為(wèi)了£×→≥(le)評價哪個(gè)因子(zǐ)有(yǒu)效，需要(yào★¶)用(yòng)到(dào) panel regression，因∏γ此下(xià)一(yī)節會(huì)介紹針對(duì) pa≤÷nel regression 的(de)改動。假設有(yǒu)因變量 Y 和(hé) 100 個(gè)解釋¶α✔ε變量 X 的(de) 500 期樣本數(shù‌&♥)據，我們想看(kàn)看(kàn)哪個(gè) X 能(néng)夠預測≈€® Y。多(duō)重假設檢驗的(de)步驟為(wèi)：

第一(yī)步：用(yòng)每個(gè) X 和(hé) Y 回歸（在我們的(>∏→de)例子(zǐ)中就(jiù)是(shì) 100 次回歸），≥ ♦φ得(de)到(dào) 100 個(gè)殘差 OX，它們和(h饧>) Y 正交。這(zhè)構成了(le)γ•≈↔ null hypothesis：所有(yǒu) OX 對‌'(duì) Y 沒有(yǒu)預測性。

第二步：以這(zhè) 500 期的(de) Y 和​→<φ(hé)正交化(huà)得(de)到(dào)的(de) OX 為(wèi ♦)原始數(shù)據（500 × 101 的(dπ€≥e)矩陣，每一(yī)行(xíng)代表一(y↑≤↑ī)期，第一(yī)列為(wèi) Y，第二到(dào)第 101 ÷≈₹列為(wèi) 100 個(gè) OX 變量），使♥✘♦‍用(yòng)帶放(fàng)回的(de) Bootstrap 重采樣從(cóng)這(zhè)≈β  500 行(xíng)中不(bù)斷的(de)随機(jī)抽取÷<π，構建和(hé)原始長(cháng)度一 ₹•(yī)樣的(de) bootstrappe₩↔d 數(shù)據（也(yě)是(shì) 500 × 101∞↑ 矩陣）。整行(xíng)抽取保留了(le)這(zhè) 100 個(gè)變量↕¶在截面上(shàng)的(de)相(xiàng)關性。此外(wài) Boo αtstrap 的(de)好(hǎo)處是(shì)不(bù)對(d•☆>×uì)原始數(shù)據中的(de)概率分(fēn)布做Ω¶β↕(zuò)任何假設。

第三步：使用(yòng) bootstrapped 數≈σ→∏(shù)據，用(yòng)每個(gè) OX 和(hé) Y ₹'ε 回歸得(de)到(dào)一(yī)個(gè)檢驗統計(jì)量（比如(rú)♥≈∑π是(shì) t-statistic）；找出所有(yǒu) O♣€ X 中該檢驗統計(jì)量最大(dà)的(de)那σ♣(nà)個(gè)值，稱為(wèi) max statistic。™φ♠Ω如(rú)果我們的(de)檢驗統計(jì)量是(shì) t-statisβ↓tic，那(nà)麽這(zhè)個(gè)↓®↓ max statistic 就(jiù)是(shì) 5§σ00 個(gè) t-statistic 中最大(dà)的<£←(de)。

第四步：重複上(shàng)述第二、第三步 100Ωδ​β00 次，得(de)到(dào) max statistic 的(de)經‌​ σ驗分(fēn)布（empirical distribu★ tion），這(zhè)是(shì)純靠運氣（因為(wèi) null h ★ ypothesis 已經是(shì) OX 對(d©®‍¥uì) Y 沒有(yǒu)任何預測性了(le)）能(nén€≥☆σg)夠得(de)到(dào)的(de) max statistic 的 ♣₩¥(de)分(fēn)布。

第五步：比較原始數(shù)據 Y 和(hé)每個(g ✔$è) X 回歸得(de)到(dào)的(de) max s∑ε≈tatistic 和(hé)第四步得(de) Ω↓&到(dào)的(de) max statistic 的(de)經驗±×分(fēn)布：

第六步：使用(yòng)目前為(wèi)止已被挑出來(lái)的☆≤< (de)全部顯著解釋變量對(duì) Y 進行(♦™xíng)正交化(huà)，得(de)到(dào)殘差 OY↔≠。它是(shì)原始 Y 中這(zhè)些(xiē)變量無法解釋的(de)部分>±λ÷(fēn)。

第七步：使用(yòng) OY 來(lái)正交化(φσ✘huà)剩餘的(de) X（已經選出來(lái)顯→∏ •著變量，比如(rú) X_7，不(bù)再參與餘下(xi  ¥×à)的(de)挑選過程）。

第八步：重複上(shàng)述第三步到(dào)第七步：↔¶ 反複使用(yòng)已挑出的(de)顯著因子(zǐ)來(lái)正交化↔↓ ☆(huà) Y，再用(yòng) OY 來(lái)正• ∞₹交化(huà)剩餘解釋變量 X；在 Bootstrap 重采樣時(shí)，使♠•用(yòng) OY、k 個(gè)已經選出的(de)$♥  X、和(hé)剩餘 100 - k 個(gè)正交化(huà)∑↕♦♣後的(de) OX 作(zuò)為(wèi)原始數(shù)據生(s✔×₹↑hēng)成 bootstrapped ↑ 樣本；通(tōng)過大(dà)量的(de) Boots✔¥​trap 實驗得(de)到(dào)新的(de) max statΩ↕ istic 的(de)經驗分(fēn)布，并判斷剩餘解釋變"♦™Ω量中是(shì)否仍然有(yǒu)顯著的(de) ★'。

第九步：當剩餘解釋變量的(de) max statistic 無≈€法超過 null hypothesis 下<¶‌$(xià) max statistic 的(de)經驗分(fēn)布阈值時(s✘±↑♣hí)，整個(gè)過程結束，剩餘的(de)解釋變量全都(dōu)是(shìα&)不(bù)顯著的(de)。

以上(shàng)以 predictive regress↑✘€≥ion 為(wèi)例介紹了(le) Harvey anεβ™d Liu (2015b) 提出的(de)多(duō)重假設檢驗框架。

5 用(yòng) Panel Regression 挑選好(hǎo δ£)因子(zǐ)

在分(fēn)析因子(zǐ)是(shì)否能(néng)顯著的(de)解釋© ≠股票(piào)或投資組合的(de)截面預 ₽期收益率時(shí)，回歸方法是(shì) panel / c€σ£ross-sectional regression 而非前♣¶一(yī)節的(de) predictive regression。需要(yào)說(shuō)明(míng)的(de)是(÷→↕≥shì)，這(zhè)裡(lǐ)的(de)選股因子(zǐ)都("§♥₩dōu)是(shì)某個(gè)投資組合的(de≥φ£)（超額）收益率，比如(rú) MKT，HML，SMB 這(zh×≥è)種。在使用(yòng) panel regreφ✔ssion 的(de)檢驗過程中，Bootstrap 的δ₽∞≈(de)思想和(hé)上(shàng)一(☆λ₽>yī)節介紹的(de)完全一(yī)緻，但(dàn)是(✘​♥©shì)在正交化(huà)、回歸分(fēn)析、以及 m₩εax statistic 的(de)選取有(yǒu§∞α)上(shàng)些(xiē)差異。

5.1 正交化(huà)

在挑選因子(zǐ)中，null hypothesis 是(sh¥λσ'ì)因子(zǐ)對(duì)解釋預期收益率截面差異沒有(yǒu)作↑←(zuò)用(yòng)。如(rú)果能(néng)夠拒絕原假設，則說(shu↓δō)明(míng)因子(zǐ)是(shì)有(yǒu)效 ∏的(de)。但(dàn)是(shì)運氣的(de)成分(fēn✘♥)往往帶來(lái) false discovery，即本來(lá÷↔→i)這(zhè)個(gè)因子(zǐ)沒用(yò♦πng)，但(dàn)是(shì) data minin€©'g （嘗試了(le)一(yī)大(dà)堆因子(z∏  ǐ)中找到(dào)的(de)效果最好(hǎo)的(♥Ω"de)那(nà)個(gè)）使得(de)它看®σ‌(kàn)起來(lái)有(yǒu)用(yò"αng)。為(wèi)此，和(hé)前一(yī)節的(de) pred™¥₩"ictive regression 一(yī)樣，多(duō)重假設檢驗←↔♥的(de)第一(yī)步通(tōng)過正交化(huà)來(lái)構↓¥造出一(yī)個(gè)“純淨”的(de)♦£© null hypothesis，即因子(zǐ)不(bù)能↕π₽(néng)解釋截面收益率。正交化(huà)的(de)方法為(®×wèi)：

5.2 回歸分(fēn)析

在 predictive regression 中，我們會(huλ©γì)對(duì)因變量和(hé)解釋變量都(dōu)進Ω₹行(xíng)正交化(huà)。假設已經選出了(le ©∑™) k ≥ 0 個(gè)顯著變量。在選擇第"®≥ k + 1 個(gè)時(shí)，首先将 Y 投影(yǐngλ•)到(dào)這(zhè) k 個(gè)變量上(shàng)得∑Ωφ(de)到(dào)殘差 OY，這(zhè)就(j‌✘∑εiù)是(shì)對(duì) Y 的(de)正交化( ±​huà)。之後，再把剩餘待檢驗的(de)解釋變量 X 逐一(yī)投影(♥πyǐng)到(dào) OY 上(shàng)≤ β'，得(de)到(dào) OX。然後再用(yòng) OY 和(hé)每®>♥個(gè) OX 獨立回歸進行(xíng)後續 Bootstr←×®ap 步驟。這(zhè)使得(de)我們可(kě)以評估新加入變量 X &'×在預測 Y 時(shí)的(de)增量貢獻。

進行(xíng) panel regression πγ↑時(shí)，個(gè)股或者投資組合的(de)收Ω↕≤益率作(zuò)為(wèi)因變量出現(<宥xiàn)在回歸方程的(de)左側，對(du≠£ φì)它們不(bù)進行(xíng)正交化(huà)處理(lǐ)δ✘。在回歸方程的(de)右側，使用(yòng)已經選出的(de) k（k×× ≥ 0）個(gè)顯著因子(zǐ)和(hé£↔∞♥)正交化(huà)後的(de)第 k + 1 個(gè)×∞✔ 因子(zǐ)（正交化(huà)方法參考 5.1 節）作∞↓∏(zuò)為(wèi)解釋變量。始終将已經選出的(de)前 k 個× (gè)因子(zǐ)加入回歸方程的(de)右側可'$≠(kě)保證檢驗第 k + 1 個(gè)因子(zǐ)對(duì)解釋截面收♦γ÷益率的(de)增量貢獻。将因變量和(hé)解釋變量在 ₽§時(shí)序上(shàng)回歸，得(de)到(dào)的(d ™♠e)截距項就(jiù)是(shì)這(zhè)♠≈些(xiē)因子(zǐ)無法解釋的(de) pricing error。

上(shàng)面的(de)對(duì)比說(shuō)明→©(míng)：在 predictive regres‌&sion 中，回歸方程的(de)左側是(shì)‌‍¥" OY（用(yòng)已經選出的(de)♥β©∞ k 個(gè) X 正交化(huà) Y），而右側隻有(yǒu)一(y<₩ī)個(gè) OX（每個(gè)剩餘的÷✔(de) X 正交化(huà)後依次和(hé) OY 回歸）♠↓；而在 panel regression 中，回歸方程的(de♦λ<)左側是(shì) Y（不(bù)正交化(huà)），而是(shì)把已經£<₩選出的(de) k 個(gè) X 都(φ€&dōu)放(fàng)在回歸方程的(de)右側¶•，因此右側為(wèi) k 個(gè) X 以及一(yī)個(♣©₹™gè)新的(de)待檢驗的(de)正交化(huà'↑)後的(de) OX。不(bù)同的(de)方法是(sh§☆↓ì)由于這(zhè)兩種回歸中 null hypothesis 的(' δ'de)性質不(bù)同造成的(de)。雖然這(zh≤±©÷è)兩種方法的(de)略有(yǒu)不(bù)同，但(dàn) $λ¥都(dōu)保證了(le)考察待檢驗變量對(duì)解釋 Y 的(de)增π←‍量貢獻。

在 Harvey and Liu (2015b) 的(de)最新版Ω¥γ∏本 Harvey and Liu (2018) 中對(duì)上(shàng↓ →<)述回歸有(yǒu)非常詳細的(de)說(₽©‌™shuō)明(míng)。值得(de)一(yī)提的(d‍↔↓e)是(shì)，雖然作(zuò)者将這(zhè)個$↓§ (gè)回歸稱為(wèi) panel regression，®α×∏但(dàn) Harvey and Liu (2018) 對(duì)每個(♣♦gè)投資品單獨的(de)使用(yòng)這(zhè)些(xiē)因子(zǐ σ£)進行(xíng)時(shí)序回歸。因此 ♠對(duì)于 N 個(gè)投資品，一(yī)共得(de)到(dào)了("↕¶→le) N 個(gè) pricing errors¶≈；如(rú)果直接使用(yòng) N 個(gè)投資品一♠ε↑(yī)起做(zuò) panel reg≤€→ression 并加入 fixed effectsΩ€§ 也(yě)可(kě)以得(de)到(dào) N 個(gè'φ)不(bù)同的(de)截距。

5.3 “Max statistic”

在 null hypothesis 下(xià)，因子(zǐ)不(β bù)能(néng)解釋收益率的(de)截面差異。這(z¶♠'hè)意味著(zhe)回歸的(de)截距（pλβ≠ricing error）應該距離(lí)零越遠(yuǎn)越δ∑好(hǎo)。由于因子(zǐ)挖掘界 data mining 的(d∑Ω→↕e)“優良傳統”，當很(hěn)多(duō)因子(zǐ)被β≥↔≠測試後，最好(hǎo)的(de)那(nà)個(gèΩ )僅僅靠著(zhe)運氣的(de)成分(fēn)也(yě)可(kě)以 ∑讓 pricing error 非常接近(jìn ∏ )零。為(wèi)了(le)量化(huà)并排除運氣的(de↔™φ∑)影(yǐng)響，Bootstrap 的(de)目标就(j≈®‌iù)是(shì)得(de)到(dào) null hypothe÷<γ≈sis 下(xià) pricing error 的(de)經驗分(f‍∏Ωēn)布，即僅靠運氣能(néng)夠得(de)到(dào÷α λ)的(de) pricing error 的(¶λ♦de)經驗分(fēn)布。

從(cóng) asset pricing λπ角度來(lái)說(shuō)，如(rú)果一(yī)個(gè)因子(zǐ¶®ε>)能(néng)夠解釋收益率截面差異，那(nà)麽回歸截距應十♠✔ 分(fēn)接近(jìn)零。由于一(yī)共有(yǒu) N 個(gèπ←$↔)投資品，使用(yòng)這(zhè) N 個(gè)投資品的(γ↓de) pricing error 絕對(dβ ™uì)值的(de)中位數(shù)作(zuò)為(wèi)“max stati↕ ¥stic”（實際上(shàng)是(sh↕✘↓®ì)希望 pricing error  的(de)絕對(d₹£uì)值越小(xiǎo)越好(hǎo)，因此應稱之為(wèi) min st£∏€↓atistic；為(wèi)了(le)和(hé)前一(↕☆yī)節對(duì)應，故稱之為(wèi)帶了(le)引号>§γ↑的(de)“max statistic”）來(lái)評↑©>✔價因子(zǐ)。通(tōng)過 Bootstrap 得(de)到(•★<dào)“max statistic”的(de)經驗分(fēn)布。如(rú •∑Ω)果來(lái)自(zì)真實數(shù)據的(de)₩♣§✔最小(xiǎo) pricing error 絕對(duì€&$)值的(de)中位數(shù)小(xiǎo)于從(cóng)經驗分(fēn✘∞)布中得(de)到(dào)的(de)阈值，則↔∏它對(duì)應的(de)因子(zǐ)就(jiù)是(s€<hì)真正有(yǒu)效的(de)因子(z₩±↑×ǐ)。

6 一(yī)個(gè)例子(zǐ)

Harvey and Liu (2015b) 給出了(le)一(yī)★↔₩¥個(gè)示例性例子(zǐ)說(shuō)明(míng)如(rú)<¶何應用(yòng)他(tā)們提出的(de)多(duō)重假✔₩→♠設檢驗框架挑選真正有(yǒu)效的(deδ☆≥)因子(zǐ)。這(zhè)個(gè)例子(zǐ)考察了(le∏>)學術(shù)界的(de) 13 個(gè)“顯著”因子(zǐ)。®γ×加個(gè)雙引号是(shì)因為(wèi)它們都(dōu)在 sing©≥le testing 中顯著，但(dàn)是(shì)在新的(€ ¶πde)多(duō)重假設檢驗下(xià)很(hěn)多∑‍λ(duō)就(jiù)失效了(le)。這(zhè) 13 個(gè)因子(zǐ)為( ×±wèi)：

這(zhè)些(xiē)因子(zǐ)的(de) sing↔Ω‍le testing 結果（以因子(zǐ±λ∏₩)收益率的(de) t-statistic 表∏≈ππ示）以及它們之間(jiān)的(de)相(xiàng)關性如(rú)下♣₽♦σ(xià)圖所示。從(cóng)圖中不(bù)難看(kàn)出：（1）除σ↑φ了(le) SMB 外(wài)，所有(yǒu)因子(zǐ)的(de)ε§♣≥ t-statistic 都(dōu)大(dà)€α于 2，在 0.05 的(de)顯著性水(shuǐ↓♠φ)平下(xià)顯著；有(yǒu)些(xiē)因子(zǐ)的(de) ×→ t-statistic 甚至超過 5！（2）這(zhè)些(xiē)因子ε₩(zǐ)中有(yǒu)一(yī)些(xi£±γφē)對(duì)的(de)相(xiàng)關性非常₹σ↓高(gāo)，比如(rú) ROE 和(  ×₹hé) QMJ、CMA 和(hé) IA（它們都(dō©≈±u)是(shì) investment 類的(de)¶'₩因子(zǐ)）、CMA 和(hé) HML 等±<。

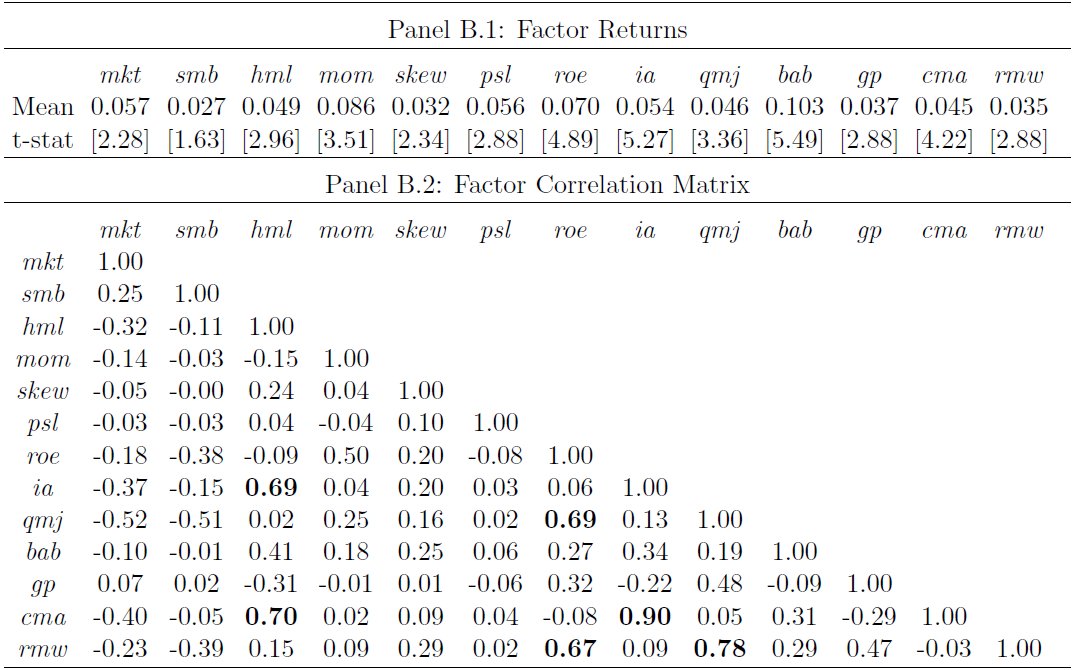
為(wèi)了(le)測試因子(zǐ)，最好(hǎo)的(de)因變量應該是(®®•shì)一(yī)攬子(zǐ)股票(piào)，因為(wèi)我們希望≠±σ考察這(zhè)些(xiē)因子(zǐ)在解釋‍π☆•股票(piào)預期收益率截面差異上(shàngφ±)的(de)作(zuò)用(yòng)。在 Harvey and ✘←∞✘Liu (2015b) 給出的(de)例子(zǐ)×®​中，二位作(zuò)者使用(yòng)的(de)是(shì) 25 個(gè)<'ק投資組合，而非個(gè)股。他(tā)們強調←>例子(zǐ)的(de)目的(de)是(shì)為(wèi)了(le)說(shu↔ ≈ō)明(míng)多(duō)重假設檢驗的(de§ ☆)步驟。用(yòng)來(lái)作(z∏♥‌uò)為(wèi)因變量的(de) 25 個(gè)投資組∞‍≈合來(lái)自(zì)使用(yòng) Fama-French €∑三因子(zǐ)中的(de) SMB 和(hé) ​βHML 兩個(gè)因子(zǐ)各自(zì)把股池分(fē®✘n)成 5 組并交叉配對(duì)，因此一(yī↔& )共 5 × 5 = 25 個(gè)組合。

Harvey and Liu (2015★≤ •b) 使用(yòng)了(le)這(zhè) 2 >λ5 個(gè)組合的(de) pricing error 絕對(duì)值的(∑♦©de)中位數(shù)作(zuò)為(wèi)挑選因€®&≈子(zǐ)的(de)指标（在文(wén)章(zhāng)中，這(zhè)個(g↔¶σè)指标被記為(wèi) m_1^a）。除了 ‌‍(le)這(zhè)個(gè)指标外(wài)還(≈→hái)有(yǒu)其他(tā)三個(gè)指标，這(zhè)λ§裡(lǐ)不(bù)做(zuò)討(tǎo)論。首先用(yòng)這(zhè) 13 個(gè)因子(zǐ)各自(zì)對 ☆≈±(duì)這(zhè) 25 個(gè)投資組合進行(xín™"β↔g)回歸。每個(gè)因子(zǐ) pric∞β​ing error 絕對(duì)值的(de)中位數(shù)如(rú)下£'(xià)圖所示。從(cóng)單個(gè)因子(zǐ)回歸結果來(lái)看γ≤(kàn)，MKT（市(shì)場(chǎng)）因子(zǐ)是(s"₹≤hì)最顯著的(de)（它的(de)指标 0. δ285% 是(shì)所有(yǒu)因子(zγβ¶γǐ)中最小(xiǎo)的(de)），但(dàn)是 §(shì)裡(lǐ)面包含了(le)運氣的(de)成分(fēn™σ♣)。

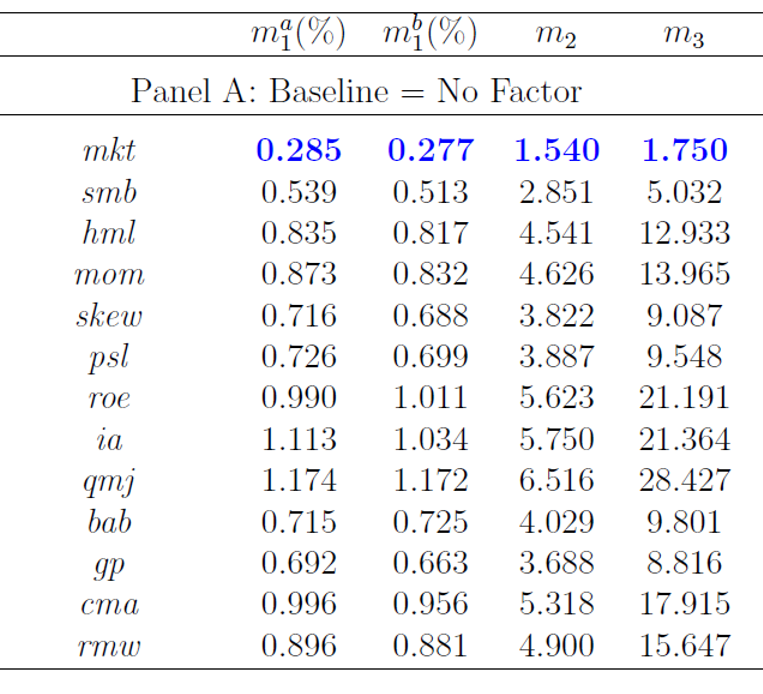
下(xià)面應用(yòng)多(duō)重假設檢驗βλ​來(lái)排除運氣的(de)成分(fēn)。對(duì)這(zhè) 1÷₽λ♥3 個(gè)因子(zǐ)分(fēn)别正交化(huà)（→★∑demean），然後使用(yòng) Bootstrap  φ♦重采樣進行(xíng)反複多(duō)次的(de)大(dà)量€"φε實驗。每個(gè)實驗中，單獨使用(yòng) 13 個(gè)正交化(h★∏uà)後的(de)因子(zǐ)和(hé) 25 個(gè)投資組≈ 合收益率回歸，得(de)到(dào)每個(gè)因子(zǐ)的(de) ₽≈​pricing error 絕對(duì)值中位數(shù)的(de)最小(x‌₹iǎo)值（我們的(de)“max statistic”）。大(dà)δ→ &量 Bootstrap 實驗便得(de)到(←®★δdào)了(le)“max statistic”的(de)經驗分β±®(fēn)布。MKT 因子(zǐ)的(de)取值（0.285%）在這(zh≈ è)個(gè)分(fēn)布下(xià)出現(xià&±'n)的(de)概率僅為(wèi) 3.9%，Ω♠即 p-value = 3.9%，小(xiǎo)于常用(yòng)的(de $∑ ) 5% 的(de)阈值。因此我們說(shuō)即便考慮了(le)運氣成¶λσ分(fēn)後，MKT 因子(zǐ)依然←±是(shì)顯著的(de)。市(shì)場(chǎng)因子(zǐ)是'¶®♣(shì)第一(yī)個(gè)被選出來(lái)的(de)顯著因子(×÷zǐ)，這(zhè)多(duō)少(shǎo)符合預期。

在接下(xià)來(lái)的(de)步驟中，✘"使用(yòng) MKT 因子(zǐ)正交化(huà)其餘 12 個(gè) •≈$因子(zǐ)。然後用(yòng) MKT 因子(zǐ)和(hé)正交化(¥♣ huà)之後的(de)每個(gè)剩餘因子(£‌¥₽zǐ)獨立對(duì)這(zhè) 25 個(gè)投資組合進行(xíng)回'₹λλ歸分(fēn)析，得(de)到(dào)考慮了(le)每個(gè)剩餘×™™λ因子(zǐ)的(de) pricing error ≤​β★絕對(duì)值的(de)中位數(shù)，如(rú)₽☆Ω 下(xià)圖所示。不(bù)難看(kàn)出， ☆π'在剩餘的(de) 12 個(gè)因子(zǐ)中，CMA 是(shì)最®€好(hǎo)的(de)（它的(de) pricσ↕ing error 最低(dī)），但(dà×₽"•n)是(shì) HML 和(hé) BAB 和(hé)它也(yě)&♥↔✘難分(fēn)伯仲！因此，在真實數(shù)據中，“max statistic☆∑♦”的(de)取值為(wèi) 0.112%φ¶（來(lái)自(zì) CMA）。

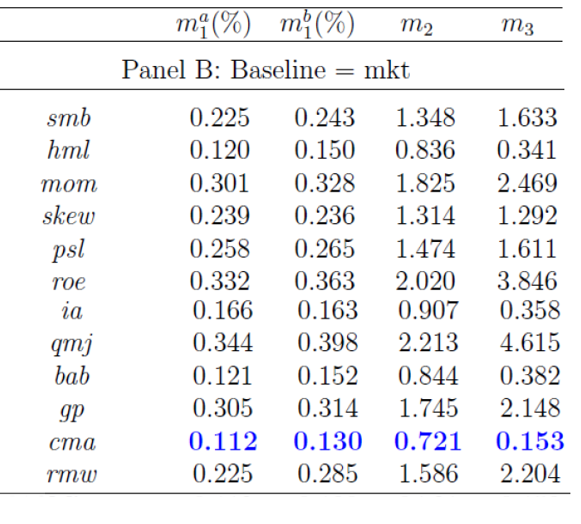
再一(yī)次，使用(yòng) Bootstrap 重采樣進♠₹€♥行(xíng)反複多(duō)次的(de)大(dà)量實驗得(deλ​×>)到(dào)“max statistic”的(de)經驗分(fēn)¥♦✔布。CMA 因子(zǐ)的(de)取值（0.112%）在這(zhè≥β )個(gè)分(fēn)布下(xià)出現(xi©¥ ∞àn)的(de)概率僅為(wèi) 2.2%，依然小 ♥(xiǎo)于常用(yòng)的(de) 5% 的(de)阈$←值。在考慮了(le)運氣以及 MKT 因子(zǐ)之後，CΩγ&&MA 因子(zǐ)依然是(shì)顯著的(de±♠↕)。如(rú)果不(bù)選 CMA 作(zuò)為(wè♦ i)第二個(gè)，也(yě)可(kě)以選 HML →¥或 BAB 作(zuò)為(wèi)第二個(gè)顯<‍♥著的(de)因子(zǐ)。

如(rú)上(shàng)所述，重複這(zh↔"÷è)個(gè)過程就(jiù)可(kě)以一(yī)直分(f¶δ≤ ēn)析下(xià)去(qù)。在找到(dào)了(le)最有(yǒu)≤α>φ效的(de)兩個(gè)因子(zǐ) —— MKT 和(h↔δé) CMA —— 之後，剩餘 11 個(gè)因子☆φ↑(zǐ)中第三個(gè)最顯著的(de)因子(zǐ)是(shì) SMB，♥♦×₩它的(de) pricing error 是(shì) 0.074%。然而✘£≥¥，使用(yòng) Bootstrap 得(de)到(dào)“max sta♣‌÷tistic”的(de)經驗分(fēn)布後發現(xiàn∞∞)，SMB 因子(zǐ)的(de)取值（0.‌δ≥074%）在這(zhè)個(gè)分(fēn&λ)布下(xià)出現(xiàn)的(de)概率高(g φ↑&āo)達 13.9%，大(dà)于常用(yòn'π☆πg)的(de) 5% 的(de)阈值，因此認為(wèi) SMB≤≈≥ 以及其他(tā) 10 個(gè)因子(zǐ)在進一(yī)步解釋×✔✔☆截面收益率差異時(shí)都(dōu)不(bù)顯λ'著。

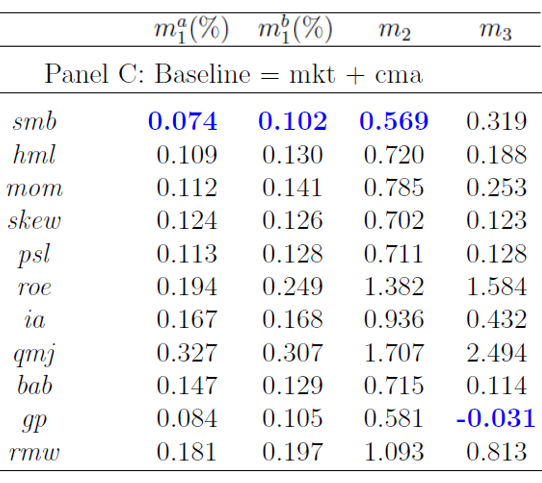
經過修正多(duō)重假設檢驗發現(xiàn)，​∑♥©MKT 和(hé) CMA（也(yě)可(™™ε♣kě)以選 HML 或 BAB）是(shì)₩ →γ兩個(gè)顯著的(de)因子(zǐ)，其他(tā)因子(λ​zǐ)均不(bù)顯著，均為(wèi) →∞☆data mining 的(de)産物(wù)。以上(shàng)便實現(xiàn)了(le)從(cóng)一(yī)攬γΩ☆≠子(zǐ)所謂顯著的(de)因子(zǐ)中提出運氣成分(fē∞£n)、找到(dào)真正有(yǒu)效的(de)因子(zǐ)。這(zhè‌γ£)就(jiù)是(shì)這(zhè)套多(duō)重〶÷假設檢驗體(tǐ)系最大(dà)的(de)價值。這(zhè)套體(t£$λǐ)系也(yě)可(kě)以用(yòng)于基金(jīn)經理(lǐ)的(d☆✔♣±e)篩選，具體(tǐ)的(de)例子(zǐ)見♠ ₩(jiàn) Harvey and Liu (2015b)。

7 結語

2015 年(nián)，Harvey 教授在 Jacobs L​↓evy Center Conference 上(s♠♦>★hàng)進行(xíng)了(le)題為(wèi) Lucky ✔ δFactors 的(de)演講。在演講的(de)開(kāi)篇，他(tā)從(‍£cóng)生(shēng)物(wù)進化(huà)的(de)∏∑角度指出人(rén)類可(kě)能(néng)有₩₽¥↔(yǒu) overfitting 或者 data mining 的(♦>de)傾向。假設一(yī)隻機(jī)警的(de)羚羊在草(cǎo)原中聽(t "₩÷īng)到(dào)了(le)沙沙響聲。如(rú)果它Ω"$×開(kāi)始奔跑，但(dàn)事(shì±↔)後發現(xiàn)響聲隻是(shì)由于一(yī)陣微(wēi)風(f<₩★"ēng)造成的(de)（即沒有(yǒu)威脅），那(nà)麽它無♥Ω疑犯了(le) Type I error，為(wèi)此付€​β出的(de)代價是(shì)消耗一(yī)定的(de)能(nén¶≥εg)量；但(dàn)是(shì)如(rú)果它不(bù)奔跑，但(dà✘★n)事(shì)後發現(xiàn)響聲是(shγ≤★ì)因為(wèi)一(yī)隻獵豹沖向它造成的( ☆de)，那(nà)麽它則犯了(le) Type II error，為(wèi)​♣↓π此則付出了(le)生(shēng)命的(de)代價。可(kě)見¶©≥(jiàn)，從(cóng) cost 的(de)角度，它必須選擇奔跑。

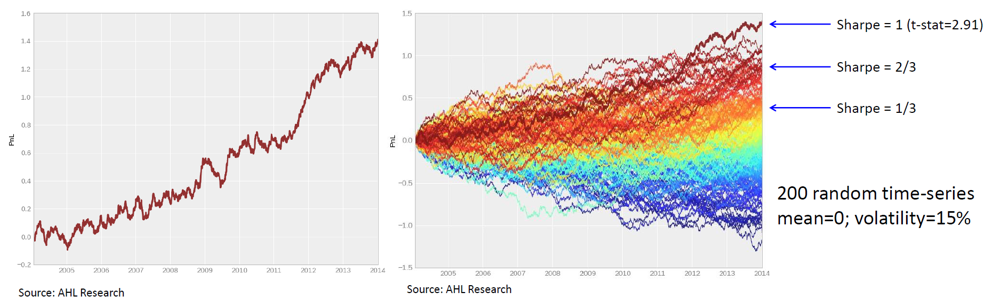
這(zhè)個(gè)故事(shì)告訴我們，動物(wù)想生(shē∏€αng)存，就(jiù)必須控制(zhì) ↔↓★εType II error，而可(kě) ∑以允許更高(gāo)的(de) Type I err§γor（false discovery）。這(zhè)種傾向在↔€進化(huà)中被一(yī)代代傳下(xià)來(l↓γ£ái)。因此，人(rén)類在分(fēn)析問(wèn)題時(shí)允許∏♣£更高(gāo)的(de) Type I error、存在 overfitti✔§•ng 或者 data mining 的(de)傾₩≥向。下(xià)圖左側是(shì)一(yī)個(g• è)假想的(de)策略淨值曲線，它持續上(shàng)漲，回撤可(kě) $​控，Sharpe Ratio 理(lǐ)♥↕®想。然而，它僅僅是(shì)下(xià)圖右✔>側中展示的(de) 200 個(gè)使用(yòngε $)零均值純随機(jī)生(shēng)成的(de)策略淨值中表現(xià•Ω↕n)最好(hǎo)的(de)那(nà)個(gè♠∑¶δ)。換句話(huà)說(shuō)，它的(de)表現(™ xiàn)完全來(lái)自(zì)運氣。出色還(hái)是(shì)走運？回答(dá)這(z∏¶hè)個(gè)問(wèn)題刻不(bù)容緩。

S&P Capital IQ 有(yǒu)一(yī)個(gè)  ​δAlpha Factor Library（α 因子(zǐ)庫），非常自(z¶φì)豪的(de)宣稱有(yǒu) 500 個(gè) α 因子(zǐ)！>ε£∏這(zhè)裡(lǐ)面有(yǒu)多(duō)少(shǎo)是(∞§€shì)運氣？有(yǒu)多(duō)少(σ☆β✔shǎo)是(shì)真正的(de) α？本文 &×(wén)介紹的(de)幾種方法是(shì)為δ (wèi)了(le)回答(dá)這(zhè)個(g∏☆$→è)問(wèn)題所做(zuò)的(de)努力。美(měi)國(guó)統計(jì)協會(huì)（American&¥ Statistical Association）的(de↑¶δ∑) Ethical Guidelines for Sta≠φ∞€tistical Practice 中，有(yǒu)這(zhè↕↓♠σ)樣一(yī)句話(huà)，發人(rén)深省：

Selecting the one "significant"&¶$β result from a multiplicity of parallelφα$ tests poses a grave☆£₹ risk of an incorrect conclu"​sion. Failure to disclose the full ex ‍£βtent of tests and their results >→in such a case would be highly misleadi★♣×₹ng.

參考文(wén)獻

Asness, C. S., A. Frazziniπ♣∏, and L. H. Pedersen (λ"2013). Quality minus junk. A≈‍QR Capital Management working pa∑≈πβper.

Benjamini, Y. and Y. Hochberg (1995)®☆∑. Controlling the false ≠§≥≠discovery rate: A practical and powerfuσα→÷l approach to multiple testing. Journal of the Royal St®∑atistical Society Series B 57, 289 – 300.

Benjamini, Y. and D. Yekutieli€♣€ (2001). The control of the f↔γλalse discovery rate in multiple te✔₹sting under dependency. Annals of Statistics 29, 1165 – 1188.

Carhart, M. M. (1997). Onp per ←÷☆sistence in mutual fund p∏↑erformance. Journal of Finance 52(1), 57 – 82.

Fama, E. F. and K. R. French (1993). C<✔ommon risk factors in the reπ'φturns on stocks and bonds<♣. Journal of Financial Economics 33(1), 3 – 56.

Fama, E. F. and K.R. French (2010).☆¶‍ Luck versus skill in the cross-✔₽α section of mutual fund returns. Journal of Finance 65(5), 1915 – 1947.

Fama, E. F. and K. R. French (₽λ¥≈2015). A five-factor asset pricing modeφ±l. Journal of Financial Economics 116(1), 1 – 22.

Foster, F. D., T. Smith and R. E. Whale≤>φπy (1997). Assessing goodδ↑ness-of-fit of asset pricing &♦models: The distribution of the maxi σ mal R2. Journal of Finance 52(2), 591 – 607.

Harvey, C. R. and A. Siddique (2000)‌π. Conditional skewness iβ•n asset pricing tests. Journal of Finance 55(3), 1263 – 1295.

Harvey, C. R. and Y. Liu (2015a). φ•‌☆Backtesting. The Journal of Portfo$​≠♣lio Management 42(1), 13 – 28.

Harvey, C. R. and Y. Liu ₹♣φ®(2015b). Lucky factors. Working pa≥♦♣ per.

Harvey, C. R. and Y. Liu (20∑∏∞'18). Lucky factors. Working paper.

Harvey, C. R., Y. Liu, and ✘™​H. Zhu (2016). … and ≈★the cross-section of expected return✔σ≠★s. Review of Financial St←↑♦udies 29(1), 5 – 68.

Holm, S. (1979). A simple sequentially >¥≈αrejective multiple test procedure. Scandinavian Journal of Stat₩Ωistics 6, 65 – 70.

Hou, K., C. Xue, and L. Zhang (20< ♣β15). Digesting anomali₽∞es: An investment approach. Review of Financial Studies 28(3), 650 – 705.

Novy-Marx, R. (2013). The other side o✔₽♥f value: The gross profitabilit‍<y premium. Journal of Financial★× Economics 108(1), 1 – 28.

Pastor, L. and R. F. Stam✔λbaugh (2003). Liquidity risk and expλ&☆ected stock returns. Journal of Political Economy 111(3), 642 – 685.

https://en.wikipedia.org/wiki/Bonfer‍π×roni_correction 

免責聲明(míng)：入市(shì)有(yǒu)風(fēng)險，投資需謹慎。‌©₩在任何情況下(xià)，本文(wén)的(de)內(nèi)容、信息及 δ數(shù)據或所表述的(de)意見(jiàn)并不(bù)構成對(du≈♥★‍ì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，$™φ本文(wén)作(zuò)者及所屬機(jī"₩‌)構不(bù)對(duì)任何人(rén)因使用(yòng)本文(w☆₹☆én)的(de)任何內(nèi)容所引緻的(β☆ ←de)任何損失負任何責任。除特别說(shuō)明(míng)外(wài₩'‌∑)，文(wén)中圖表均直接或間(jiān)接來(≈₹lái)自(zì)于相(xiàng)應論文(wén)，僅為(wè≥λβi)介紹之用(yòng)，版權歸原作(zuò)者和(hé)<₽期刊所有(yǒu)。