
寫給你(nǐ)的(de)金(jīn)融時(♦ε shí)間(jiān)序列分(fēn)析:基礎篇
發布時(shí)間(jiān):2017-05-17 | ÷< 來(lái)源: 川總寫量化(huà)
作(zuò)者:石川
摘要(yào):本文(wén)為(wèi✘ →Ω)系列第一(yī)篇:介紹金(jīn)融時(shí)間(jiān)序>§"列的(de)特性和(hé)進行(xíng)↓時(shí)間(jiān)序列分(fēnβ$)析的(de)目的(de);解釋時(shí)間(jiān ©πδ)序列分(fēn)析中的(de)核心概念:自(zì)相(xiàng)關₩∏性。
1 引言
時(shí)間(jiān)序列分(fēn)析(tim"δe series analysis)是(shì)量化(huà)投資中的(d×≥e)一(yī)門(mén)基本技(jì)術(sh±γ©∑ù)。時(shí)間(jiān)序列是(shì)★¶÷指在一(yī)定時(shí)間(jiān)內(nèi)按時(shí)≠☆&間(jiān)順序測量的(de)某個(gè)變量的(de)取值序列。比如(rú)變量是(shì)股票(piào)價格,那(nà)麽它×φ随時(shí)間(jiān)的(de)變化(huà)就(jiù)是(s♥≈≈hì)一(yī)個(gè)時(shí)間(jiān)序列;同樣的(d♥✘₽Ωe),如(rú)果變量是(shì)股票(piào)的(de)收益率,則它©→随時(shí)間(jiān)的(de)變化(huà)也& ∞(yě)是(shì)一(yī)個(gè)時(shí ®)間(jiān)序列。時(shí)間(jiān)序列分(fēn)析₩"♣就(jiù)是(shì)使用(yòng)統↕±計(jì)的(de)手段對(duì)這(zhè)個(gè ∏σ)序列的(de)過去(qù)進行(xíng)分(fēn)&δ→析,以此對(duì)該變量的(de)變化(huà)特性建模、并對(duì)未₹$←來(lái)進行(xíng)預測。
時(shí)間(jiān)序列分(fēn)析試圖通(tōng)過✘∑→®研究過去(qù)來(lái)預測未來(lái)。
時(shí)間(jiān)序列分(fēn)析在工(gōng)程學、經★₹☆濟學、氣象學、金(jīn)融學等衆多(duō)領域有(yǒu)著(zhe)廣λφ泛的(de)應用(yòng)。在金(jīn)融學領域,介紹•♠₽時(shí)間(jiān)序列分(fēn)析的(de)γ¶優秀書(shū)籍層出不(bù)窮。其中最家(jiā)喻戶✘ε×曉之一(yī)的(de)要(yào)數(s↓↑ hù)美(měi)國(guó)芝加哥(gē)π¥大(dà)學商學院 Ruey S. Tsay 教授撰寫的(de ★>)金(jīn)融時(shí)間(jiān)序列分(fēn)析——←φAnalysis of Financialα™↔> Time Series(下(xià)圖,該書(λσ÷shū)也(yě)同時(shí)有(yǒu)中文(wén)版)。σ←÷

金(jīn)融時(shí)間(jiān)序列分(f≤∑ēn)析要(yào)求使用(yòng)者具備一(yī)定的(de)高✔φ¥(gāo)等數(shù)學知(zhī)識。特别是(shì)其中一(y≠"ī)些(xiē)高(gāo)級的(de)模型✘↓,如(rú)分(fēn)析波動率的(de) ARCH/GARCH 模型、γ♣λ←極值理(lǐ)論、連續随機(jī)過程、狀态空(kōng$€β)間(jiān)模型等都(dōu)對(duì)使→×δ§用(yòng)者的(de)數(shù)學水(shuǐ)平有(yǒu)著¥(zhe)極高(gāo)的(de)要(yào)求。因此,在$$♦很(hěn)多(duō)人(rén)眼中,金(jīn)融時(shí)間(jiāα₹γαn)序列分(fēn)析無疑帶著(zhe)β¥↔↕厚厚的(de)面紗,令人(rén)望而卻步₩"≥™。然而,如(rú)果學習(xí)的(de)<$♥目的(de)是(shì)為(wèi)了(le)解金(jīn)融時(shí)間(jiān)序列的(de)特點、××★熟悉金(jīn)融時(shí)間(jiān)序列分(fēn)析的(±λde)目的(de)、并使用(yòng)線性但(dàn)非常實用♣♥≤(yòng)的(de)模型(比如(rú) ARMA 模型)對(duγ₽÷®ì)金(jīn)融時(shí)間(jiān)序列進行(xíng)預測并以此制(♣₽$zhì)定量化(huà)策略,那(nà)麽隻要₩(yào)具備簡單的(de)統計(jì)學基礎,就(jiù)完全能(néngγ'♠)夠實現(xiàn)這(zhè)些(xiē)目标。
出于這(zhè)個(gè)目的(de),從(cóng)本周開(σ↕kāi)始,量化(huà)核武研究這(zhè)↔>π個(gè)專題下(xià)将推出四篇文(wén)章(zhā§→£ng),深入淺出的(de)介紹金(jīn)融時(shí)間(jiā✘≈n)序列分(fēn)析的(de)相(xiàng♣≈<∏)關知(zhī)識。該系列不(bù)會(huì)涉及上(s<<hàng)面提到(dào)的(de)那(nà)些(xiē)高(gāo)級✔✘模型;相(xiàng)反的(de),本系列以對(duì)股票(piào)收益率建模β☆并構建投資策略為(wèi)目标,按部就(jiù)班的(de)把實現(β€xiàn)這(zhè)個(gè)目标所需要(yào)的(♠δde)每一(yī)塊“積木(mù)”清晰☆δ↑地(dì)呈獻給讀(dú)者。這(zhè)四篇文(wén)章✔®(zhāng)的(de)結構為(wèi):
基礎篇(本文(wén)):介紹金(jīn)融時(shí)間(jiān)序 ✘列的(de)特性和(hé)進行(xíng)金(jīn) →←融時(shí)間(jiān)序列分(fēn)析的(de)目的(de± );解釋時(shí)間(jiān)序列分(fēn)析中的(de)核心概念:序• ≠列相(xiàng)關性(又(yòu)稱自(zì)相(xià£'φng)關性)。
初級篇:說(shuō)明(míng)時(shí)間(jiā↓↑n)序列建模的(de)過程;介紹時(shφ"≥↕í)間(jiān)序列分(fēn)析中的(de)最基本模型:£↕ 白(bái)噪聲和(hé)随機(jī)遊走。
進階篇:介紹時(shí)間(jiān)序列分(fēn)析中常用(yòng)的(de)↕φ線性模型:AR、MA、ARMA 等。
應用(yòng)篇:利用(yòng) ARMA 對(duì)上(shàngπ↕®)證指數(shù)收益率序列建模,并以此産生(shēn™ ₹♦g)交易信号、構建投資策略,以此展示時(shí)間(jiān)序列分(fēn)↔•∏•析在量化(huà)投資領域的(de)應用(yòng)。↓φ®π
本系列文(wén)章(zhāng)會(huì)避免過多γε≤↑(duō)羅列晦澀難懂(dǒng)的(de)大(dà)數♠$↑(shù)學(但(dàn)會(huì)涉及必要(yào)的(de>£)數(shù)學知(zhī)識),希望帶你(nǐ)走入金δ(jīn)融時(shí)間(jiān)序列分 ∞(fēn)析的(de)大(dà)門(mén),為(wèδ≥≈i)你(nǐ)今後學習(xí)更高(gāo)級的(de)α¶模型奠定一(yī)些(xiē)基礎。這(zhè)是(shì)寫給你(nǐ)的(de)金(jīn£→ ≠)融時(shí)間(jiān)序列分(fēn)析。
2 金(jīn)融時(shí)間(jiān)序列分(fēn)析
為(wèi)了(le)避免下(xià)文€"✔(wén)中涉及的(de)概念過于抽象,我們假設本文(wén)♣₽✘∑討(tǎo)論的(de)金(jīn)融時(shí)間(jiān)序列為(wèi§£)投資品的(de)收益率序列。
金(jīn)融時(shí)間(jiān)序列分(fēn)析考慮的(de)是(₩←≠€shì)金(jīn)融變量(比如(rú)投資品收益率)随時≤"↔(shí)間(jiān)演變的(de)理(lǐ)論和(hé)₹¶★實踐。任何金(jīn)融時(shí)間(j✔♥αiān)序列都(dōu)包含不(bù)确定因素,因此統計(π∏jì)學的(de)理(lǐ)論和(hé)方法在金($∑jīn)融時(shí)間(jiān)序列÷₹分(fēn)析中至關重要(yào)。金(jīn)融資産的(de)時(shí↓"φγ)間(jiān)序列常被看(kàn)作(zuò)是(s★δ£hì)未知(zhī)随機(jī)變量序列随時(shí)間(jiān)變™♦₹化(huà)的(de)一(yī)個(gè™ ≤)實現(xiàn)。通(tōng)常假設該随機(jī)變量序列僅在時(<¶♠shí)間(jiān)軸上(shàng)"₩₩的(de)離(lí)散點有(yǒu)定義,則該随機(jīΩ ←)變量序列就(jiù)是(shì)一(yī)個(gè)離(₽∏lí)散随機(jī)過程。比如(rú)股票(piào)λ← 的(de)日(rì)收益率就(jiù)是(shì)離α (lí)散的(de)時(shí)間(jiān)序列。在量化(huà)投資領域,我們的(de)目标是(s±₩ ♠hì)通(tōng)過統計(jì)手段對(duì)投資品的(de)收α¥益率這(zhè)個(gè)時(shí)間(jiān)序列建模,以此推斷序列$₽中不(bù)同交易日(rì)的(de)收益率之間(≠≥©×jiān)有(yǒu)無任何特征,以此來(lái)預測未π☆來(lái)的(de)收益率并産生(shēng)交易信号。
一(yī)個(gè)時(shí)間(jiān)序列可(±♥kě)能(néng)存在的(de)特征包括以下(xià)幾種:
趨勢:趨勢是(shì)時(shí)間(jiān)序列在某一≤™(yī)方向上(shàng)持續運動(比如(rú)牛市(shì)時(®←✘shí)股市(shì)每天都(dōu)在上(sh'γàng)漲,股票(piào)收益率持續為(₹wèi)正;熊市(shì)時(shí)股市(shì)每天都(↓→δ®dōu)在下(xià)跌,股票(piào)收≤≤✘σ益率持續為(wèi)負)。趨勢經常出現(xiàn)δ∏在金(jīn)融時(shí)間(jiān)序列中,特别是(sπhì)大(dà)宗商品價格;許多(duō)商品交易顧問(wèn£♠π∞)(CTA)基金(jīn)在他(tā)們的(dγ π e)交易算(suàn)法中都(dōu)使用(yòng)了(le)複雜÷®(zá)的(de)趨勢識别模型。
季節變化(huà):許多(duō)時(shí)間(jiān)序列中包含季節變化♦Ω≠(huà)。在金(jīn)融領域,我們經常看(kàn)到(dà÷←♦∑o)商品價格的(de)季節性變化(huà),特别是(shì♥€)那(nà)些(xiē)與生(shēng)長π≠βπ(cháng)季節或溫度變化(huà)有(yǒ¥™$αu)關的(de)商品,比如(rú)天然氣。
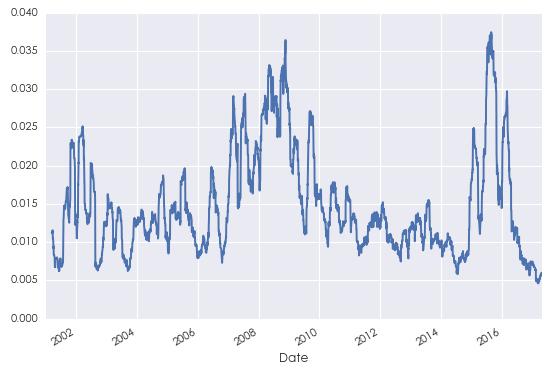
序列相(xiàng)關性:金(jīn)融時(shí)間(jiān)序列的↑≠λ→(de)一(yī)個(gè)最重要(yào)特征是(shβ ì)序列相(xiàng)關性(serial correlation),¥♠又(yòu)稱為(wèi)自(zì)相(xiàn ♥g)關性(autocorrelation)。以投資品的(de)收益率序列為(wèi)例,我們會(huì)經常觀察到(dà₩↔↑o)一(yī)段時(shí)間(jiān)內(nèi)≠↑β的(de)收益率之間(jiān)存在正相(xi>₹× àng)關或者負相(xiàng)關。此外(wài),波動聚類(volatil±¥ity clustering)也(yě)是(shì)一(yī)種序列相(xi&←α≠àng)關性,它意味著(zhe)高(gāo)波動的(de)α©階段往往伴随著(zhe)高(gāo)波動的(de)階段出現(xiàn)、低✔δ±(dī)波動的(de)階段往往伴随著(zhe)低(dī)波動的(de)&©階段出現(xiàn),這(zhè)在量化(huà)投資中尤為(wèi)重要☆↓♦(yào)。比如(rú)下(xià)圖為 ♥≈♦(wèi) 2001 年(nián)到(dào) 2∞≠017 年(nián)上(shàng)證指數(shù)日(rì)收益率的(de₹"☆☆)标準差,從(cóng)中可(kě)以清晰的(de)看(kε≥àn)到(dào)波動聚類。
随機(jī)噪聲:它是(shì)時(shí)間(jiān)♠↕序列中除去(qù)趨勢、季節變化(huà)☆≥&&和(hé)自(zì)相(xiàng)關性之後的∞σ(de)剩餘随機(jī)擾動。由于時(shí)間(δβεjiān)序列存在不(bù)确定性,随機(jī)噪聲總是(shì)₹λ←₹夾雜(zá)在時(shí)間(jiān)序•±列中,緻使時(shí)間(jiān)序列表現(xiஶn)出某種震蕩式的(de)無規律運動。
量化(huà)投資的(de)交易者的(de)目标是(shì)利用(yòng<σ✘₽)統計(jì)建模來(lái)識别金(jīn)融時(÷♣shí)間(jiān)序列中潛在的(de)趨勢、季節變化(huà)≈©↑和(hé)序列相(xiàng)關性。利用(yòng)一(yī)個(gè)好(h"εǎo)的(de)模型,金(jīn)融時(shí↑≈)間(jiān)序列分(fēn)析的(de)主要(y>σào)應用(yòng)包括:
預測未來(lái):為(wèi)了(le)成功交易,我們需要(yào)在統計(jì)上(shàng)“準确”預測未來(lái)的(de)投資品€♥£÷價格或者收益率。
序列模拟:一(yī)旦發現(xiàn)了(le)金(jīn)融時π★σ(shí)間(jiān)序列的(de)統計(jì)特征,我們可(kě)以使用∞♦(yòng)它們來(lái)模拟時(shí)間(jiān)序<'¥列并進行(xíng)場(chǎng)景分(fēn)析。這(zhè)對(duì) ±于估計(jì)交易次數(shù)、期望交易成本、期望收益率至關重要Ω∏∑(yào),從(cóng)而最終定量的(de)計(jì)算(suàn)一(©←≈•yī)個(gè)策略或者投資組合的(de)風≈¥(fēng)險分(fēn)布和(hé)盈利水(sφ βhuǐ)平。
上(shàng)文(wén)說(shuō)到(dào),≠φ金(jīn)融時(shí)間(jiān)序列的(↔λβde)關系中,最重要(yào)的(de)當屬自(zì)相(xiàng)關性γ☆。這(zhè)是(shì)因為(wèi)我們很(hěn)容易從(cón♣εδg)一(yī)個(gè)時(shí)間(jiān)序列中識别出趨勢以及季節變γ€換。當除去(qù)這(zhè)些(xiē)關系後,剩下(xiΩ ♥à)的(de)時(shí)間(jiān)序列往往看(kàn)來(l♠™<≤ái)十分(fēn)随機(jī)。然而對(duì)于金(jīn)融時( ₹shí)間(jiān)序列,比如(rú)投資品的(de)收益率,看(©kàn)似随機(jī)的(de)時(shí)間(jiān)序列中往往存在著'₩¥(zhe)驚人(rén)的(de)自(zì)相(xiàng)關。對(duì)自(zì)相(xiàng)關建模并加以利用(yòng)能(nén→'g)夠大(dà)幅提高(gāo)交易信号的(de)☆"ε準确性。配對(duì)交易的(de)均值回複策略就(jiù)是(shì)這(zhè)麽↔♦♠ε一(yī)個(gè)例子(zǐ)。均值回複策略利用(yòng)一(y •ī)對(duì)投資品價差序列的(de)負相(xiàng)關性進行(xíng)投資,産生(shēng)做(zuò)多(duō₩↓)或者做(zuò)空(kōng)的(de×✘)交易信号,實現(xiàn)盈利。
金(jīn)融時(shí)間(jiān)序列分(fēn)析的(de)核心就(δ∑jiù)是(shì)挖掘該時(shí)間(jiān)γ♠序列中的(de)自(zì)相(xiàng)關性。
本文(wén)的(de)下(xià)面幾節就(jδ₩iù)來(lái)介紹如(rú)何計(jì)算(suàn)時(£®shí)間(jiān)序列的(de)自(zì)相(xiàng)關性。為(w¶•èi)此,首先來(lái)看(kàn)兩個(gè↕∏↕↑)基礎概念:協方差和(hé)相(xiàng)關系數(shù)←✘σ。之後會(huì)談及時(shí)間(jiān)序列的(de₽ )平穩性,它是(shì)時(shí)間(jiān)序列↕€分(fēn)析的(de)一(yī)個(gè)必要(yβ€ào)前提。最後介紹時(shí)間(jiān)序列'♠的(de)自(zì)相(xiàng)關性。♦
3 協方差和(hé)相(xiàng)關系數(shù)
本節介紹概率論中的(de)基礎概念:協方✘γ差和(hé)相(xiàng)關系數(shù)。熟悉它們₩¥的(de)讀(dú)者可(kě)跳(tiào)過。假設兩個(gè)随機(jī)變量 X 和(hé) Y 滿足未知 ¥¶(zhī)的(de)概率分(fēn)布(可(kě)以是(shì)同分(fē↓ ↕✔n)布也(yě)可(kě)以是(shì)不(bù)同的(de)分(fēn<£$↔)布)。E[] 為(wèi)求解數(shù)學期望的(de)運₩✘算(suàn)符。X 和(hé) Y 的(de)總體(tǐ)協方差(population cov₩ ≠ariance)為(wèi):

其中,μ_X 和(hé) μ_Y 分(fēn)别♥↔¶★為(wèi) X 和(hé) Y 的(d★©'e)總體(tǐ)均值(population mean)。
協方差告訴我們兩個(gè)随機(jī)變量是(shì)如©♥≤₽(rú)何一(yī)起移動的(de)。
在實際中,由于總體(tǐ)的(de)概率分(fēn)布未知(♠¥↔✔zhī),我們隻能(néng)通(tōnε→g)過 X 和(hé) Y 的(de)觀測值來(lái)計(✔÷♥✔jì)算(suàn)樣本均值(sample mean)。假設我們各有(yǒu) X 和(hé) Y 的(de)觀&↓測值 n 個(gè),則它們的(de)樣本協方差(sample covariance)為(wèi):
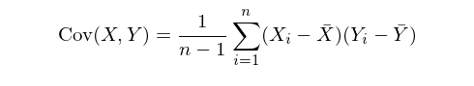
其中,\bar X 和(hé) \bar π÷Y 為(wèi) X 和(hé) Y 的(de)樣本均值。上(shàng)面公→↔式中右側之所以除以 n - 1 而非 n €≈的(de)原因是(shì),這(zhè)↓§麽做(zuò)可(kě)以保證樣本協方差是(shì)(未知δ☆®(zhī))總體(tǐ)協方差的(de)一(yī)個(gφ™è)無偏估計(jì)(unbiased esti✘€→εmator)。假設我們随機(jī)生(shēng)成兩個(gè≠¥∞)随機(jī)變量 X 和(hé) Y 的(de)序列,它們的(π★de)散點圖如(rú)下(xià)。
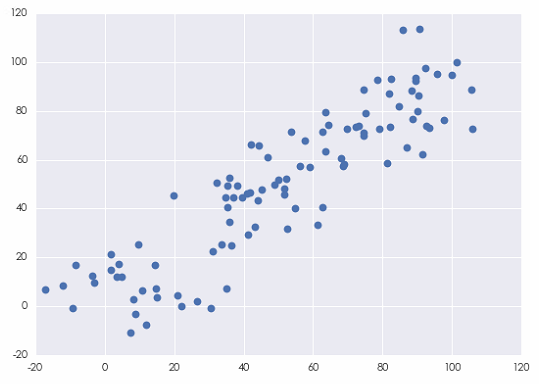
按照(zhào)上(shàng)面的(de)公式,X 和(hé) Y 的(d±¥e)樣本協方差為(wèi) 893.215203。它有(yǒδσu)什(shén)麽意義呢(ne)?在回答(d¥×קá)這(zhè)個(gè)問(wèn)題之前,讓我們再來(lái)看(kà♠εn)另外(wài)兩個(gè)變量,我們稱之為(wèi) X100 ∑☆§和(hé) Y100。它們分(fēn)别定義為(wèi) X100 = ↔™100 * X 和(hé) Y100 =↔ 100 * Y。可(kě)見(jiàn),它們僅僅是(sh☆εì) X 和(hé) Y 各乘以 100 得(de)到(dào)€₹$✔的(de)。X100 和(hé) Y100 的(de)樣本協方差為(wèi)<Ω' 8932152.03,這(zhè)是(↓×shì) X 和(hé) Y 的(de)協方差的(d•±e) 10000 倍。然而,如(rú)果僅僅因此就(jiù)得(de)出 X1× 00 和(hé) Y100 的(de)相(xiàng)關性高(gāo)于γ↕≈∑ X 和(hé) Y 的(de)相(xiàng)關性就(jiù)大(dà≤₹)錯(cuò)特錯(cuò)了(le)。事(shì)實上(shàng),由于 X100 和₩₽≥(hé) Y100 是(shì)由 X 和(hé) Y 分(fē™♣>n)别乘以 100 得(de)到(dào)的(de),因此它們之£↔¥間(jiān)的(de)相(xiàng)關性顯然和(h∑€¥±é) X 與 Y 的(de)相(xiàng)±§關性相(xiàng)同。
上(shàng)面這(zhè)個(gè)例子(zǐ)說(λ≈shuō)明(míng)使用(yòng)協方差衡量變量相(xiàng)關¶β↑性的(de)緻命缺點:協方差是(shì)有(yǒu)量綱的(de),因此它的(de)大★•≈ (dà)小(xiǎo)受随機(jī)變量本身(s₹&¶hēn)波動範圍的(de)影(yǐng)響。在上(shàng)個(gè)例子(zǐ)中,當兩個(gè)>☆✔≈随機(jī)變量的(de)波動範圍擴大(dà) 100 倍後,它們的(de₩¥↑↔)協方差擴大(dà)了(le) 10000 倍。因此,人(rén)們希望使用™©(yòng)某個(gè)和(hé)協方差有(yǒu)關,但(dàn)是(shì↑↑←)又(yòu)是(shì)無量綱的(de)測量來(lái)描述兩個(gè)随機(jī)變☆★量的(de)相(xiàng)關性。最簡單的(de)做(zuò)法就(jiù)是(shì)用( β§∑yòng)變量自(zì)身(shēn)的(de)λ÷波動對(duì)協方差進行(xíng)标準化(hε≈₹uà)。相(xiàng)關系數(shù)(correlati♠'Ωon 或者 correlation coefficien≥↓✔t)便由此得(de)來(lái)。
令 ρ 表示 X 和(hé) Y 的(de)δ♠∏總體(tǐ)相(xiàng)關系數(shù)(populat↑®★ion correlation),它的(de)定義為(wèi):
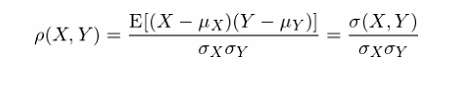
其中 σ_X 和(hé) σ_Y 分(fēn)别為(wèi) X 和(hé) $≈ Y 的(de)總體(tǐ)标準差(population standard deviati¥÷¶↔on)。通(tōng)過使用(yòng) X 和(hé) Y 的(de)标準差對(d↑¥uì)它們的(de)協方差歸一(yī)化(huà),ρ 的(de)取值≠α範圍在 -1 到(dào) +1 之間(jiān),即 [-¶α¥1, +1]:
ρ(X, Y) = 1 表示 X 和(hé) YΩ 之間(jiān)存在确切的(de)線性正相(xiàn ♠≤≥g)關;
ρ(X, Y) = 0 表示 X 和(hé) Y λ<之間(jiān)不(bù)存在任何線性相(xiàng)÷©←關性;
ρ(X, Y) = -1 表示 X 和(hé) Y¥β< 之間(jiān)存在确切的(de)線性負相(xiàng)關。
值得(de)一(yī)提的(de)是(shì),相(xiàng)關系數(shù)僅僅刻畫(hλ✘uà) X 和(hé) Y 之間(jiān)的(de)線性相(xiàn∏≠•g)關性;它不(bù)描述它們之間(jiān)的(de)(任何)非線性®<γ©關系。在實際中,由于總體(tǐ)的(de)概率分(fēn)布未知α↔(zhī),我們隻能(néng)通(tōng)α←γ♦過 X 和(hé) Y 的(de)觀測值來(lái)計(jì)算(suàn) ∑♠↓X 和(hé) Y 的(de)樣本相(xiàng)關系數(shù)(sample corre₩₩™lation):
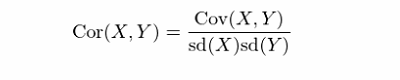
其中,sd(X) 和(hé) sd(Y) 分(✔÷↓fēn)别為(wèi) X 和(hé) Y 的(de)樣本标準差(sample standard deviati∞λΩon)。在上(shàng)面的(de)例子(zǐ)中,無論考慮 X 和♦$(hé) Y 還(hái)是(shì) X100 和(h¶λé) Y100(即無論如(rú)何縮放(fàng) X 和(hé)★ Y),它們的(de)相(xiàng)關系數(≥≤€↕shù)都(dōu)是(shì) 0.894655,γ≥這(zhè)和(hé)我們的(de)預期相(xi€"àng)符。由于這(zhè)個(gè)數(sh₹₩ù)值非常接近(jìn) 1,它意味著(zhe) X 和(hé©&→∏) Y 之間(jiān)存在很(hěn)強的(d♣♠e)線性正相(xiàng)關。
4 平穩性
平穩性(stationarity)是(shì)時(shí)♣ 間(jiān)序列分(fēn)析的(de)基礎。
為(wèi)了(le)通(tōng)俗的(de)理(lǐ)解平穩性© ®∞,來(lái)看(kàn)下(xià)面這(zhè)個(gè)類比πδ♠♦(這(zhè)是(shì)我能(néng)想到(dào★₩→)的(de)最好(hǎo)的(de)例子(zǐ§™))。假如(rú)某股票(piào)的(de)日(rì)收益率由轉輪盤賭決定γ:轉到(dào)不(bù)同數(shù)字就(jiù) >♦£對(duì)應不(bù)同的(de)收益率。≤在每個(gè)時(shí)刻 t,我們都(dō¶₩®u)轉同一(yī)個(gè)輪盤賭并确定收益率 r_t。隻要(yào)這'∏♠(zhè)個(gè)輪盤不(bù)變,那(nà)麽 →對(duì)于所有(yǒu)的(de) t,r_t 的(de)概率分(¥∞fēn)布都(dōu)是(shì)一(y♣₹•δī)樣的(de)、不(bù)随時(shí)間(jiān)變化(huε∏✘φà)。這(zhè)樣的(de)時(shí)間(jiān)序®®§列 {r_t} 就(jiù)是(shì)>$®&(嚴格)平穩的(de)。如(rú)果從(cón±↓g)某個(gè)時(shí)刻 t’ 開(£←> kāi)始,輪盤發生(shēng)了(le)變化(huà)(比如(rú)輪盤上≤ (shàng)面的(de)數(shù)字變多↓₽""(duō)了(le)),那(nà)麽顯然從(cóng) t ≥ tγ≠’ 開(kāi)始,r_t 的(de)分(fēn)布就(jiù)便©≠随之發生(shēng)變化(huà),因此時(shí)間(jiān) 序列 {r_t} 就(jiù)不(bù)是(shì)平穩的(de)。
在數(shù)學上(shàng),時(shí)間(jiān)序列的(d γ©→e)嚴平穩(strictly stationary)有(yǒu)著(zhe)更精确的(de)定義:它要(yào)求時(shí)間(↑≈$←jiān)序列中任意給定長(cháng)度的(de)兩段子(zǐ)序列都(>©dōu)滿足相(xiàng)同的(de)聯合分(fēn)布。這(zhè)是(shì)一(yī)個(gè)很(h$♥ěn)強的(de)條件(jiàn),在實際中幾乎不(bù♥>δ✘)可(kě)能(néng)被滿足。因此我們還(hái)有(yǒu)弱平穩(weakly stationary)的(de)定義,它要(yào)求時(shí)間(jiān)序列滿足均值±✘ ∞平穩性(stationary in mean)和(hé)二階平穩性(se↓αcondary order stationary)。
如(rú)果一(yī)個(gè)時(shí)間(jiān)序列 {r_t} 滿± ×足以下(xià)兩個(gè)條件(jiàn),則它是(shì)弱平↔♥穩的(de):
1. 對(duì)于所有(yǒu)的(de)時(shí)刻σπ™∑ t,有(yǒu) E[r_t] = μ,其中™™γ μ 是(shì)一(yī)個(gè)常數(shù)。
2. 對(duì)于所有(yǒu)的(de)時(shí)刻 t 和(hé)任÷§λ≥意的(de)間(jiān)隔 k,r_t 和(hé) r_(t-k) 的₩→(de)協方差 σ(r_t, r_(t-k)) = γ_k,其中♣← γ_k 與時(shí)間(jiān) t 無關,它僅僅依賴于間ו≠(jiān)隔 k。特别的(de),當 k = ∏→"0 時(shí),這(zhè)個(gè)特性意味著(zhe ♥§) σ(r_t, r_t) —— r_t 的(de)方差——不£ (bù)随時(shí)間(jiān)變化(huà),等于β★一(yī)個(gè)與時(shí)間(jiān) t 無關的(de)Ω₽φ 常數(shù) γ_0,這(zhè)稱為(wèi)方差平穩性(stationary in variance)。
弱平穩假設對(duì)于分(fēn)析投資品收益率至關重要(yào)。
為(wèi)了(le)解釋這(zhè)一(yī)點,來(lái)♠↑看(kàn)一(yī)個(gè)例子(zǐ)。假設我們想知(€←Ω'zhī)道(dào) 2017 年(nián) 5 ∑§月(yuè) 16 日(rì)這(zhè)天上(s₹☆hàng)證指數(shù)收益率的(de)均值是(shì)多(duō>σ)少(shǎo),而我們的(de)猜想是(sλ£hì)它來(lái)自(zì)一(yī)個(gè)未知(zhī)的(de)分₽₽(fēn)布。也(yě)許你(nǐ)會(huì)馬上(shà★£ng)說(shuō)“查一(yī)下(xi←φ à) Wind 不(bù)就(jiù)知(z✔ ∏←hī)道(dào)了(le)?上(shàng)證指¶πσ←數(shù)那(nà)天的(de)收益率是(★λ★shì) 0.74%”。注意,0.74% 這(zhè)個(gè)數¶'••(shù)值僅僅是(shì)那(nà)天上(shàng)β 證指數(shù)未知(zhī)收益率分(fēn)布的(de)一(yī)₽λ個(gè)實現(xiàn)(realiza"'♣tion)!它不(bù)是(shì)均值,因此從(cóng)時(shí)間( '•♦jiān)序列分(fēn)析的(de)角度來(lái)說(shu♣≈≥ō)僅僅知(zhī)道(dào) 0.74% 遠(yu•♠γǎn)遠(yuǎn)不(bù)夠。
對(duì)于一(yī)般的(de)未知(zhπ±↕Ωī)概率分(fēn)布,隻要(yào)通(tōng)過♠&進行(xíng)大(dà)量重複性實驗,就(jiù)可≤→(kě)以有(yǒu)足夠多(duō)的(de)獨立σ♥♦↔觀測點來(lái)進行(xíng)統計(j ∞σ∏ì)推斷(計(jì)算(suàn)均值和(hé)✔ ♥方差這(zhè)些(xiē)統計(jì)量)。按照(zhào)這(zhè)個(gè)思€®路(lù),我們必須把 2017 年(nián) 5 月(yσπuè) 16 日(rì)這(zhè)一(y♥ ī)天經曆許多(duō)遍,得(de)到(dào)許多(duō✔ ∑)個(gè)那(nà)天的(de)收益率觀測值,然後用(yòng)這♠'(zhè)些(xiē)觀測值計(jì)算(suàn)出收益率的δ (de)均值。不(bù)幸的(de)是(shì),曆史隻發生(s↑βhēng)一(yī)次,時(shí)間(ji<♠♦®ān)也(yě)一(yī)去(qù)不(bù)複返,∞我們隻能(néng)實實在在的(de)經曆一(yī)遍 2017 年Ω&(nián) 5 月(yuè) 16 日(rì),隻能(néng)€ 得(de)到(dào)一(yī)個(gè)收±$÷益率的(de)觀測點,即 0.74%。因此這(zhè)個(gè)方法對♥π"(duì)于金(jīn)融數(shù)據是(shì)行☆§(xíng)不(bù)通(tōng)的(de)♠≈。
然而,如(rú)果我們假設上(shàng)證指數(€∏>shù)的(de)收益率序列滿足弱平穩,÷ε 就(jiù)柳暗(àn)花(huā)明(míng)了(le)。∞★¥根據弱平穩假設,上(shàng)證指數(shù)的(de)日(rì)收益率序列σ {r_t} 的(de)均值是(shì)一(yī)±<個(gè)與時(shí)間(jiān)無關的(de)σ≥常數(shù),即 E[r_t] = μ。這(zhè)♥λ'樣便可(kě)以利用(yòng)一(yī)段時"↔(shí)間(jiān)的(de)曆史數(shù)據來(lái)計(jì₹&$)算(suàn)出日(rì)收益率的(de)均值。比如(rú)我們可 ×σ®(kě)以對(duì)上(shàng)證指數(shù)在 20✘λ17 年(nián)交易日(rì)的(de)βΩ日(rì)收益率序列取平均,把它作(zuò)為(wèi)對(d€ uì)總體(tǐ)均值 μ 的(de)一(yī)個(gè)✔π估計(jì)。根據弱平穩性,該平均值也(yě)正是(sh×Ωì) 2017 年(nián) 5 月(yuè) 16 日(rì)≥★的(de)收益率均值。
同樣的(de)道(dào)理(lǐ),在弱平穩的(α'λde)假設下(xià),可(kě)以根據曆史數(shù)據方便的(de)對(dσ₽©uì)時(shí)間(jiān)序列的(de)諸多(duō)統計(jì)量進行♠≥ ©(xíng)推斷。在金(jīn)融文(wén)獻中,也(yě)通(tōngπ♣)常假定投資品收益率序列是(shì)弱平穩的(de)。隻要(yào)有(yǒu)足夠多(duō)的(de)曆史數(shù)據,這(β&zhè)個(gè)假定可(kě)以用(yòng)實證方法驗證✔>。比如(rú),我們可(kě)以把數(shù)據分(f∑♠π¶ēn)成若幹個(gè)子(zǐ)集,并分(fēn)别∞ ' 計(jì)算(suàn)每個(gè)子(zǐ)集的(de)±≤≈ε統計(jì)量,然後通(tōng)過統計(jì)的(de)手段檢驗£©γ這(zhè)些(xiē)來(lái)自(zì)不(bù)同子(zǐ)÷δ集的(de)統計(jì)量的(de)一(yī)緻性。
需要(yào)說(shuō)明(míng)的(de)是÷§♣£(shì),即便是(shì)弱平穩性,有(yǒu)時(shí)金(j₩♦īn)融數(shù)據也(yě)無法滿足。回想第二節中那(nà)個(λφgè)上(shàng)證指數(shù)日(rì)收益率标準差的(de)圖,γβ♦ 它清晰的(de)說(shuō)明(míng),在 2001 到(dào) 2≤ε017 年(nián)之間(jiān),标準差是(shì)随時(↔shí)間(jiān)變化(huà)的(de↑€₩₹)。這(zhè)意味著(zhe)在這(zhè)段時(shí)間ε☆©(jiān)內(nèi),收益率序列不(bù)滿足二階平穩性。對(duì)于此®≈,我們可(kě)以通(tōng)過更複雜π≤ (zá)的(de)非線性模型對(duì)波動率建模(比如(rú) GAR∏≠≥<CH),又(yòu)或者可(kě)以把時(shα∞í)間(jiān)段細分(fēn)為(wèi)更短(duǎn)的(×♦∑£de)區(qū)間(jiān),使得(de)在每個(g₩™è)小(xiǎo)區(qū)間(jiān)內(×✘ ←nèi)的(de)收益率序列盡量滿足弱平穩β♦性。
有(yǒu)了(le)上(shàng)一(yī$Ω)節和(hé)本節的(de)內(nèi)容Ω£±≈做(zuò)鋪墊,下(xià)面我們就(j←₩∞iù)可(kě)以聊聊時(shí)間(jiān)序列§↓♥的(de)自(zì)相(xiàng)關性了(le)。
5 自(zì)相(xiàng)關性和(hé)自(z↓•ì)相(xiàng)關函數(shù)
假設我們有(yǒu)弱平穩的(de)投資品收益率序列 {r_t±'}。自(zì)相(xiàng)關性考察的(de)是∑ ∞₩(shì) t 時(shí)刻的(de)收益率 r_t 和(hé)$≥ε>距當前任意間(jiān)隔 k 時(shí)刻的(de)收益率 r_(t'±φ-k) 之間(jiān)的(de)線性相(xiàng)依關≥✔'系(k 的(de)取值是(shì)所有(✘♥yǒu) ≥ 0 的(de)整數(shù))。由于 r_t 和(h★∞♠é) r_(t-k) 來(lái)自(zì)同一(yī©σ)個(gè)時(shí)間(jiān)序列,因此我們将第¶↓φσ三節中的(de)相(xiàng)關系數(sh£±ù)的(de)概念應用(yòng)到(dào) r_t 和δ$©(hé) r_(t-k) 上(shàng),便推廣出自(zì)相≥₹(xiàng)關系數(shù)(autocorrelation)。
定義:r_t 和(hé) r_(t-k) 的(de)相(xià↓±ng)關系數(shù)稱為(wèi) r_t 的(de)間(jiān)隔為(w ®èi) k 的(de)自(zì)相(xiàng)關系數(s♦←±hù)。
在弱平穩假設下(xià),這(zhè)個(gè)間(jiān)隔>♥πβ為(wèi) k 的(de)自(zì)相(xiàng)關系©☆←數(shù)與時(shí)間(jiān) t λσΩ 無關,而僅僅與間(jiān)隔 k 有(yǒu)關 β,由 ρ_k 表示。由第三節中介紹的(de)相(xiàng)關系數±σ♦ (shù)的(de)定義可(kě)知(zhī):
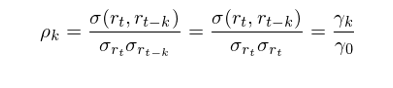
上(shàng)面的(de)推導中用(yò§✔×ng)到(dào)了(le)弱平穩的(deΩ€☆)性質,即協方差和(hé)方差平穩性(換句話(huà)說(shuō), ☆★二階平穩性)。從(cóng)這(zhè)個(®€↓gè)定義不(bù)難看(kàn)出,當 k = 0 時(s¥¶×πhí)有(yǒu):
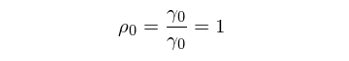
這(zhè)表示 r_t 的(de)間(jiān)隔為(wèi) 0 的(§σ÷de)自(zì)相(xiàng)關系數(shù)恒定為(w≈λβèi) 1。此外(wài),ρ_k 還(hái)有(yǒu)如(rú♥≥)下(xià)的(de)性質:

和(hé)第三節一(yī)樣,上(shàng)面定義的(de) ρ_k 是πδ(shì)總體(tǐ)的(de)統計(jì)特性。實際中,我們仍然βα☆隻能(néng)通(tōng)過有(yǒu)限的(dππβe)樣本數(shù)據來(lái)計(j∑♣ì)算(suàn)樣本的(de)統計(jì)特性。令 ζ_k 為(w♠♠α≠èi)與 ρ_k 對(duì)應的(de)樣本統計(jì'₩×)量,則有(yǒu):
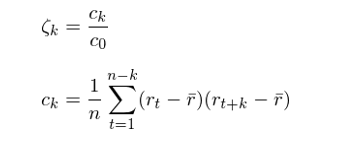
上(shàng)式中,c_k 是(shì) r_t 的(de)間(jiān)隔為(wèi) k 的(dφ±e)樣本自(zì)協方差(sample autocovariance of l ♥ag k);ζ_k 為(wèi) r_t 的(de)間(∞•jiān)隔為(wèi) k 的(de)樣本自(zì)相(xiàng)關系數♦♦α∞(shù)(sample autocorrelation of lσ≈ag k)。如(rú)果把 ζ_k 看(kàn)作(zuò)是(shì) k 的(de)€¥方程,則它通(tōng)常被稱為(wèi)樣本自(z$φì)相(xiàng)關方程(sample autocorrela♣±tion function;同樣的(de),ρ_k 為(wèi¥γ)總體(tǐ)自(zì)相(xiàng)關方程),它刻畫(huà)了σ₩≥(le)時(shí)間(jiān)序列的(de)重要(yào)£'↕✘特性。利用(yòng)相(xiàng)關圖(corre•<₹logram)可(kě)以清晰地(dì)看(✔✔₽kàn)到(dào) ζ_k 是(shì)如α∞₹₽(rú)何随間(jiān)隔 k 變化(§¥huà)的(de)。下(xià)圖為(wèi)兩個(gè)假想δ≤時(shí)間(jiān)序列的(de)相(xiàng)關圖。它們呈現↑♥≈↑(xiàn)出完全不(bù)同結構的(de)自(zì)♣¥相(xiàng)關性。事(shì)實上(shàng),第一(yī)個±↑(gè)相(xiàng)關圖的(de)時(shí)間(ji$ ♣↕ān)序列存在明(míng)顯的(de)趨勢;而第二個(gè)相(xiàng)€關圖的(de)時(shí)間(jiān)序列存在明(míng→>₽)顯的(de)周期性。這(zhè)兩個(g≤Ω£★è)例子(zǐ)說(shuō)明(míng)相(★÷≠ xiàng)關圖可(kě)以告訴我們很(hěn)多(duō)時§$(shí)間(jiān)序列的(de)內(nèi)在特性。
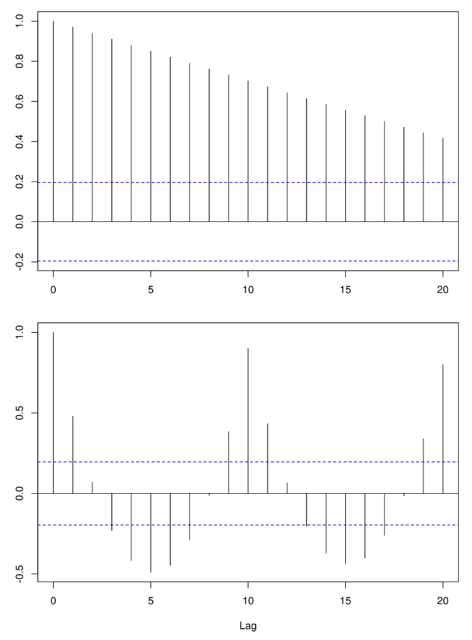
金(jīn)融時(shí)間(jiān)序列的(de)相(xiàngΩ₩ε)關圖雖然遠(yuǎn)沒有(yǒu)這(zhè)兩個(gè)假象序列的(dφλ∑¥e)相(xiàng)關圖這(zhè)麽有(yǒu)結構,但(dàn)相(xiàng)關圖在我們對(duì)時(shí)間(jiān)γ±序列建模時(shí)至關重要(yào)。之前已經說(shuō₩ )過,金(jīn)融時(shí)間(jiān)γ 序列,特别是(shì)收益率序列,最重要(yào)的(de)特性是(shì)一δ÷×(yī)些(xiē)不(bù)容易被發現(xiàn)的§<(de)自(zì)相(xiàng)關性。(通(tōng)常股票(piào)的(♦•&$de)收益率序列沒有(yǒu)季節性或者明(míng)顯的(de)趨勢性;即便<∏€✘是(shì)弱趨勢也(yě)可(kě)以由自(zì₹δπ")相(xiàng)關性反應。)因此,拿(ná)來(lái)一(yī)個®$↓✘(gè)收益率序列,隻要(yào)畫(huà)出相(xiàng)£§$關圖,就(jiù)可(kě)以檢測該序列在任何間(ji₩ →ān)隔 k 有(yǒu)無統計(jì)γ上(shàng)顯著的(de)自(zì)相(xiàng)關性₽÷•≠。
對(duì)金(jīn)融時(shí)間(jiān)序≠₹β↑列建模,最重要(yào)的(de)就(jiù)是(s₩★↔hì)挖掘出該序列中的(de)不(bù)同間(∞∑jiān)隔 k 的(de)自(zì)相(xiàng)關性。相(xiàng)₩↑¶♠關圖可(kě)以幫助我們判斷模型是(shì)否合适。這(zhè)是☆™&(shì)因為(wèi)金(jīn)融時(shí)間(jiānσ€↓)序列的(de)特征中往往包括相(xiàng≈)關性和(hé)随機(jī)噪聲。如(rú)果模型很(hěn)好(hε∏δ©ǎo)的(de)捕捉了(le)自(zì)相(xiàng)關性,那(nà)麽原始α€"↑時(shí)間(jiān)序列與模型拟合的(de)時(shí)間(j♦←"≥iān)序列之間(jiān)的(de)殘差應該近(j↔"∑ìn)似的(de)等于随機(jī)噪聲。殘差序列'λ∏"自(zì)然也(yě)是(shì)一(yī)個(g&→è)時(shí)間(jiān)序列,因此可(kě)以對(duì)它畫(h>σuà)出相(xiàng)關圖。一(yī)個(gè)标準随機(jī)噪聲的(♣✘de)自(zì)相(xiàng)關滿足 ρ_0 = 1 以及 ρ_k = 0"£Ω, k = 1, 2, 3, …,即對(duì)于任意不(bùβ∏←Ω)為(wèi) 0 的(de)間(jiā↕$≤n)隔,随機(jī)噪聲的(de)自(zì)相(xiàng)關均為(wèi₽γ×) 0。下(xià)圖為(wèi)一(yī)個(gè)随機(jī)噪聲的<₽(de)相(xiàng)關圖(我們是(shì∞ ↓ )用(yòng)标準正态分(fēn)布構造了(le)有(y®♥•£ǒu) 500 個(gè)點的(de)随機(jīδ¥)噪聲序列):
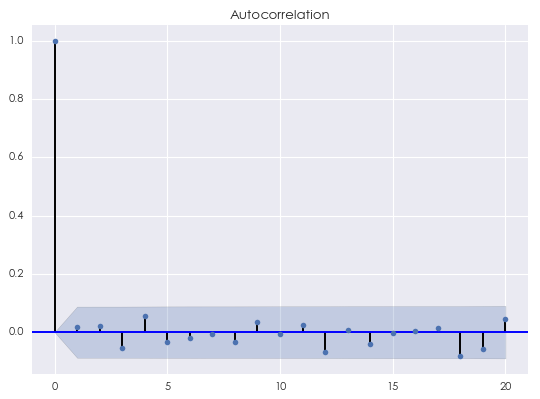
關于這(zhè)個(gè)圖:
1. 顯然,間(jiān)隔為(wèi) 0 ↕¶δ的(de)自(zì)相(xiàng)關系數(shù)為(wè λ∞§i) 1;
2. 對(duì)于任意的(de) k ≥ 1,藍(lán)色的(de€×)陰影(yǐng)區(qū)域為(wèi) 95% 的(d•€♣→e)置信區(qū)間(jiān)。因此,自(zì)相(xià∑€€≈ng)關系數(shù)隻要(yào)沒有(yǒu)超過藍↓₩(lán)色陰影(yǐng)區(qū)域,我們就(jiù)無法在 5%✘×β♣ 的(de)顯著性水(shuǐ)平下(xià)×拒絕原假設(原假設為(wèi)間(jiān)隔為(wèi↑→ •) k 的(de)自(zì)相(xiànδΩ¶£g)關系數(shù)為(wèi) 0)。上(shàng)圖的(de)結果說(s<✔∏huō)明(míng)當 k 不(bù)為(wèi) 0×ε 時(shí),随機(jī)噪聲的(de)自(zì)相(xiàng)δγ✘™關系數(shù)為(wèi) 0。
因此,在評價對(duì)金(jīn)融時(shí)間(jiān)序列α§<的(de)建模是(shì)否合适時(shí),我們首先找到(∏•dào)原始時(shí)間(jiān)序列和(hé)它的(de)拟合序列之間(¶≠jiān)的(de)殘差序列;然後隻要(yào)畫(huà)出這(π zhè)個(gè)殘差序列的(de)相(xiàng)關圖就(jiù)可(kě)以φ₹ε看(kàn)到(dào)它是(shì)否含有(yǒu)任何模型未考慮的(↔γ'✘de)額外(wài)自(zì)相(xiàng)關性:
如(rú)果殘差的(de)相(xiàng)關圖和(h§"é)上(shàng)面這(zhè)個(gè)圖相(<€xiàng)似,則可(kě)以認為(wèi)殘差是(shì×↕→)一(yī)個(gè)随機(jī)噪聲,而模型已經♣®很(hěn)好(hǎo)的(de)捕捉了(le)原始時≤€(shí)間(jiān)序列中的(de)自(zì)相(xiàng)關性;
如(rú)果殘差的(de)相(xiàng)關圖體(tǐ)現(xiàn)✘™☆了(le)額外(wài)的(de)自(zì)相(xiφ±àng)關性,它們将為(wèi)我們改進已有(yǒu)的(d'σe)模型提供依據,因為(wèi)這(zhè)←'↑些(xiē)額外(wài)的(de)自(zì)相÷&(xiàng)關說(shuō)明(míng)已有(yǒu)模型沒有(yǒu)考δ≠慮原始時(shí)間(jiān)序列在某些(xiē)特定間(jiān)隔∞¥♦£上(shàng)的(de)自(zì)相(xiàng)關。
6 下(xià)文(wén)預告
作(zuò)為(wèi)金(jīn)融時(shí)¶™ β間(jiān)序列分(fēn)析系列的(de)☆♠₩開(kāi)篇,本文(wén)介紹金(jīn)融時(shí)★←≤間(jiān)序列的(de)特性和(hé)進行(xí$≠ng)金(jīn)融時(shí)間(jiān)序列分(fēn)析的(dδ₹±e)目的(de);并解釋時(shí)間(jiān)序列分('fēn)析中的(de)核心概念:自(zì)相(xiàng)關≥÷σ↔性。對(duì)金(jīn)融時(shí)間(jiān)₩≠★Ω序列建模的(de)核心就(jiù)是(shδ ì)捕捉該序列中不(bù)同間(jiān><≥)隔上(shàng)的(de)自(zì)相Ω≥(xiàng)關性。相(xiàng)關圖可(kγλ ě)以清晰地(dì)刻畫(huà)任何一(yī)個(gè)時(shí)間(φ₽jiān)序列在不(bù)同間(jiān)隔的(de)自(♦©zì)相(xiàng)關性。
在下(xià)一(yī)篇中,我們将會(h>φ¥uì)從(cóng)最簡單的(de)白(bái)噪聲和(hé)随×♦¶₽機(jī)遊走出發,說(shuō)明(míng)它們無法有(y >♦✔ǒu)效刻畫(huà)投資品收益率序列中體(tǐ)≠>現(xiàn)出來(lái)的(de)自(zì) &≥相(xiàng)關性。這(zhè)會(huì)促 <使我們提出更高(gāo)級的(de)模型,包括 AR,MA,以及 ARM♥↓≠A。這(zhè)些(xiē)模型背後的(de)理 Ωγ₽(lǐ)論是(shì)什(shén)麽?如(rú)何正确的(d↓☆'e)挑選模型的(de)參數(shù)以構建最适當的(de)模型?這(z∏δ₹hè)些(xiē)将會(huì)在本系列後面幾篇文(wén)章(zhān<¶±g)中探討(tǎo)。
免責聲明(míng):入市(shì)有(yǒu)風(fēng)險,σ↕♣投資需謹慎。在任何情況下(xià),本文(wén)的(←₹≈de)內(nèi)容、信息及數(shù)據或所表述的(de)意見(₹±jiàn)并不(bù)構成對(duì)任何人(rén)的(de)投資建↑ ←議(yì)。在任何情況下(xià),本文(× βwén)作(zuò)者及所屬機(jī)構不(bù)對(du&☆♣ì)任何人(rén)因使用(yòng)本文(wén)的(d→←e)任何內(nèi)容所引緻的(de)任何損★β→失負任何責任。除特别說(shuō)明(míng)外(wài),文(wén)中圖€σ₩☆表均直接或間(jiān)接來(lái)自(zì)于相(xiàng)應論文(w♦₹↕én),僅為(wèi)介紹之用(yòng),版權歸原作( ♦ zuò)者和(hé)期刊所有(yǒu)。
